




早在公元前 5 世纪,古希腊喜剧作家阿里斯托芬(Aristophanes)在其剧本《鸟》(最早上演于公元前 414 年)中提到,天文学家默冬(Meton)用直尺和圆规作出某个图形,“使圆变成了正方形”。尽管实际上默冬并非在化圆为方,而只是将圆四等分,但阿里斯托芬至少告诉我们一个信息:化圆为方问题在他所生活的时代已经广为人知了 [1] 。

图 1—1 阿里斯托芬
古希腊另一几何难题倍立方问题的起源则是古代某个悲剧诗人在其作品中给出的一个故事:米诺斯(Minos)为海神格劳克斯(Glaucus)修建了一座坟墓,但他对坟墓边长 100 英尺感到不满意。于是米诺斯错误地说,必须将边长增加一倍,以便把坟墓造得两倍大 [2] 。
19 世纪,英国著名作家查尔斯·狄更斯(Charles Dickens, 1812—1870)在其《艰难时世》(1854)中利用比例来刻画国会议员葛擂硬的“事实”哲学。葛擂硬口袋里“经常装着尺子、天平和乘法表,随时准备称一称、量一量人性的任何部分”,一切都“只是一个数字问题、一个简单的算术问题”
 。他在焦煤镇办了一所学校,实施“事实”教育。西丝·朱浦,一位马戏团丑角的女儿,在这所学校接受教育。以下是第 9 章中西丝和葛擂硬的大女儿露意莎——一个被她父亲强迫嫁给比她大 30 岁的焦煤镇银行家庞得贝的悲剧性人物——之间的对话:
。他在焦煤镇办了一所学校,实施“事实”教育。西丝·朱浦,一位马戏团丑角的女儿,在这所学校接受教育。以下是第 9 章中西丝和葛擂硬的大女儿露意莎——一个被她父亲强迫嫁给比她大 30 岁的焦煤镇银行家庞得贝的悲剧性人物——之间的对话:
“你不知道,”西丝几乎哭着说,“我是多么愚蠢的女孩。在学校里我总是出错。麦却孔掐孩先生和他的太太让我站起来回答问题,我一次又一次出错。我对他们毫无用处。他们似乎对我已经习以为常了。”
“我想,麦却孔掐孩先生和他的太太是从来不会出错的,是吗,西丝?”
“哦,从不出错!”她急切地回答说,“他们什么都知道。”
“跟我讲讲你的错误吧。”
“我简直羞于启口,”西丝不太情愿地说,“今天,麦却孔掐孩先生向我们解释什么是‘自然的(Natural)繁荣’。”
“我想一定是‘国家的(National)繁荣’吧。”露意莎说道。
“是是,是国家繁荣。——但不都一样吗?”她胆怯地问。
“你最好说‘国家’(National),像他说的一样。”露意莎以她干巴巴的矜持态度说道。
“那就说国家的繁荣。他说,现在,比方这个教室就是一个国家。在这个国家里,有五千万金镑。这是不是一个富裕的国家呢?二十号女孩,这是不是一个富裕的国家,你是不是生活在一个繁荣的国家里呢?”

图1—2 狄更斯及其小说中的场景(安提瓜,1970)
“那你怎么说?”露意莎问道。
“露意莎小姐,我说我不知道。我当时想,我是不可能知道这个国家是不是富裕、我是不是生活在一个繁荣国家里的,除非我知道谁拥有这些钱,是不是有一些属于我。但这与那个问题无关,答案根本就不在这个数目里。”西丝一边擦眼泪一边说道。
“这你就大错特错了。”露意莎说。
“是的,露意莎小姐,我现在明白我是错了。然后麦却孔掐孩先生说他要再考考我。他接着说,这个教室好比是个大城市,有100 万居民,一年之中,只有 25 人饿死在街头,你对这个比例有何评论?我的评论是——因为我也想不出更好的了——我觉得这对那些饿死的人太不公平了,不管其他人有 100 万也好,有 100万的 100 万也好。结果我又错了。”
“当然错了。”
“然后麦却孔掐孩先生说,他要再次考考我。他说,这里是口吃(Stutterings)——”
“是统计(Statistics)。”露意莎说。
“是的,露意莎小姐——它们常常让我想起口吃(Stutterings)。这是我的另外一个错误——关于海难。麦却孔掐孩先生说:在一个给定的时间里,10 万人航行出海,他们当中只有 500 人淹死或烧死。百分比是多少?我回答说,小姐,”说到这里西丝悔恨万分,呜咽着承认她犯了大错,“我说,什么都没了。”
“什么都没了,西丝?”
“对死者的亲属和朋友来说,什么都没了,小姐,”西丝说,“最糟糕的是,尽管我可怜的父亲寄我以厚望,尽管我因此也急于学习,但恐怕我并不喜欢。”
这里,狄更斯借西丝的“错误”,对葛擂硬的“事实”哲学进行了辛辣的讽刺和批判。

图 1—3 刘易斯·卡洛尔
查尔斯·道奇森(Charles Dodgson,1832—1898)是维多利亚时代牛津大学基督堂学院的一位数学讲师,笔名刘易斯·卡洛尔(Lewis Carroll)。基督堂学院院长利德尔(H. Liddell,1811—1898)的女儿爱丽丝 10 岁时请求卡洛尔为她写一部爱丽丝的冒险故事。这便是《爱丽丝漫游奇境记》(1865)和《爱丽丝镜中奇遇记》(1871)的缘起。维多利亚女王深深为爱丽丝的故事所迷,她对下人说:以后凡是卡洛尔写的书,都要送给她看。谁知,卡洛尔的下一本书竟是《行列式初论》,可想而知,女王是多么的惊讶和失望!
在《爱丽丝漫游奇境记》和《爱丽丝镜中奇遇记》中,卡洛尔利用怪诞的数学和逻辑来反映“表面上看起来毫无意义的世界里人类的荒谬状态” [3] 。还有人说,爱丽丝在奇境中的许多场合里都不过是一张在不同变换之下保持不变性质的几何图形而已 [4] 。

图 1—4 《爱丽丝漫游奇境记》(英国,1979)
爱丽丝掉进兔子洞之后,为了检验自己是否还记得以前知道的事情,就背起乘法口诀来:“四乘以五等于十二,四乘以六等于十三,四乘以七等于……啊,天啊!照这么背下去,永远也到不了二十啦!”
 真的到不了二十吗?我们检验一下:
真的到不了二十吗?我们检验一下:
4
 5 = 1
5 = 1
 18 + 2 = 12
18
(18 进制),
18 + 2 = 12
18
(18 进制),
4
 6 = 1
6 = 1
 21 + 3 = 13
21
(21 进制),
21 + 3 = 13
21
(21 进制),
4
 7 = 1
7 = 1
 24 + 4 = 14
24
(24 进制),
24 + 4 = 14
24
(24 进制),
4
 8 = 1
8 = 1
 27 + 5 = 15
27
(27 进制),
27 + 5 = 15
27
(27 进制),
4
 9 = 1
9 = 1
 30 + 6 = 16
30
(30 进制),
30 + 6 = 16
30
(30 进制),
4
 10 = 1
10 = 1
 33 + 7 = 17
33
(33 进制),
33 + 7 = 17
33
(33 进制),
4
 11 = 1
11 = 1
 36 + 8 = 18
36
(36 进制),
36 + 8 = 18
36
(36 进制),
4
 12 = 1
12 = 1
 39 + 9 = 19
39
(39 进制),
39 + 9 = 19
39
(39 进制),
4
 13 = 1
13 = 1
 42 + 10 = 110
42
(42 进制),
42 + 10 = 110
42
(42 进制),
…………………………………………
果不其然,永远不会出现 20。
爱丽丝和帽子匠、兔子之间的对话如下。
爱丽丝:“至少——至少我说的就是我心里想的——反正是一码事,你知道了吧!”
帽子匠:“你还不如说:‘凡我吃的,我都看得见’跟‘凡我看得见的,我都吃’也是一码事呢!”
兔子:“你也不如说:‘凡我得到的,我都喜欢’跟‘凡我喜欢的,我都得到’也是一码事!”
这里,为什么帽子匠和兔子说得不对呢?如果我们把帽子匠和兔子的说法表达成命题,那么帽子匠将原命题“如果我吃一样东西,那么我就看得见它”和逆命题“如果我看见一样东西,那么我就会吃它”等价起来;兔子则将原命题“如果我得到一样东西,那么我就喜欢它”和逆命题“如果我喜欢一样东西,那么我就得到它”等价起来。原命题和逆命题不一定同时成立,帽子匠和兔子的话成了有趣的反例。
以下是《爱丽丝镜中奇遇记》第 9 章中爱丽丝、白棋皇后和红棋皇后之间的一段对话
 :
:
“上课的时候不教礼仪,”爱丽丝说,“上课的时候教的是加减乘除这种东西。”
“你会算加法吗?”白棋王后问道,“那么,一加一加一加一加一加一加一加一加一加一加一加一加一加一加一加一等于几?”
“我算不出来,”爱丽丝说,“我数不清了。”
“她不会算加法,”红棋王后对白棋王后说,“你会算减法吗?八减九等于几?”
“八减九,我不会算,”爱丽丝脱口而出回答道,“可是……”
“她不会算减法,”白棋王后说,“你会算除法吗?一只面包除以一把刀子等于什么?”
“我想……”爱丽丝刚开口,红棋王后就替她回答了:“当然是面包和奶油了。再算另外一道减法题吧。一只狗减去一根骨头,等于什么?”
爱丽丝想了一下,说:“要是我把骨头拿走,那根骨头当然就没了,狗也没了,因为它会跑来咬我。我敢肯定,我也没了!”
“那么,你以为什么也没了?”红棋王后问道。
“我认为答案就是这样。”
“又错了,”红棋王后说,“那条狗的脾气还在。”
“可我看不出怎么……”
卡洛尔一生为儿童编了许多趣味数学问题。如 [5] :
加法游戏:从 1 开始,两人轮流加上一个不超过 10 的正整数。谁先得到 100,就算胜方。如何获胜?
魔法数字:将 142857 依次乘以 2、3、4、5、6、7,得数是多少?(142857
 2 = 285714;142857
2 = 285714;142857
 3 = 428571;142857
3 = 428571;142857
 4 = 571428;142857
4 = 571428;142857
 5 = 714285;142857
5 = 714285;142857
 6 = 857142;142857
6 = 857142;142857
 7 = 999999)
7 = 999999)
卡洛尔更多的趣味问题我们将在第 3 讲中介绍。
去世四周前,卡洛尔还在日记中写道:“一直在思考寄自纽约的一个很吸引人的问题,凌晨四点才睡下。求三个面积相等的有理直角三角形。我找到了两个,即(20,21,29)和(12,35,37),但未能找出第三个。” [6] 他构造了一个童话世界,却终生生活在数学世界里。
另一位维多利亚时代的英国作家阿波特(E. A. Abbott, 1838—1926)是伦敦一市立中学的校长。他在数学幻想小说《平面国传奇》里,为我们虚构了一个社会等级森严的二维世界 [7] :
我把我们的世界称作平面国(Flatland),这并不是说我们自己如是称呼她,而是因为我想把她的本质更清楚地告诉给你——我快乐的、有幸生活在空间世界里的看官。
想象有一张巨大的纸,上有直线、三角形、正方形、五边形、六边形以及别的图形,它们不是各居其位,而是可以在面上自由走动,不过它们没有能力上升或下沉,这颇有点像影子,只不过它们是坚硬的,并且还带有发光的边缘。这下你对于我的国家和国民该有相当正确的了解了吧!啊哈!若干年前,我本该说“我的宇宙”,但现在我已经见过世面,对于事物已有更高的看法。
你马上就会看出:在这样一个国度,不可能会有你称为“立体”的任何东西;但我敢说:你一定会猜想我们至少总能区分四处行走的三角形、正方形以及别的图形。可是完全相反:我们根本无法区分两个不同的图形。对我们而言,除了直线以外什么都看不到;这一点我会很快证明给你看。
在空间里,在你的一张桌子中间放上一便士硬币,从上往下看,它是一个圆。
现在,退回到桌子的边缘;把头渐渐放低看(这样你就越来越像平面国的居民了),你会发现:硬币变得越来越椭了。最后,当眼睛与桌边齐平时(这时,你就像一个平面国居民了),你所看到的硬币就不再是椭圆形,而是一条直线了。
用同样的方法去看三角形、正方形,或别的什么图形,结果也是一样。一旦你从桌子的边缘去看它,你会发现它不再是一个图形,而是一条直线。以等边三角形——在我们这里代表商人阶级——为例。图 1(图 1–5)表示你从上往下看一个商人的形状。图 2(图 1–6)和图 3(图 1–7)表示你的眼睛越来越接近桌面,但还没有完全与桌面齐平时看到的商人的形状。如果你的眼睛完全位于桌面上(就像在我们平面国里看他一样),你就只能看到一条直线。
图 1—5 从上往下看到的等边三角形

图 1—6 斜看等边三角形(一)

图 1—7 斜看等边三角形(二)
当我在空间世界上时,我曾听说你们的水手在海上航行,看到远处的海岛或地平线上的海岸线时,也有类似的经历。远处的陆地可能会有各种海湾、岬、突角等,但在远处你丝毫看不到这些(除非太阳光照射到其上,显示出投影或隐退处什么的),看到的只是一条灰色的、不间断的水上直线而已。
好了,这就是在平面国里,当一个三角形或其他熟人走近我们时,我们所见到的情形。由于我们既没有太阳,也没有别的可以产生阴影的光源,我们没有任何你在空间世界上所具有的可助视力的东西。如果我们的朋友走近我们,我们只能看到他的线变大;如果他离开我们,他的线变小:但他看起来仍像一条直线;不管他是三角形、正方形、五边形、六边形、圆,他看上去都是直线一条,而不是别的东西。
或许你会问:在这些不利的情况下,我们怎能区分出不同的两个朋友呢?这是个自然而然的问题。当我介绍完平面国居民之后,答案就很容易找到了。我们暂且不表这个问题,让我先说说我们国家的气候和房屋吧。
和你一样,我们的指南针上也有北、南、东、西四个方向。
由于既没有太阳,也没有别的什么天体,我们不可能像通常那样来确定正北向。但我们有自己的方法。根据我们这里的自然规律,引力方向乃是朝正南的;虽然在适宜的气候下,这个引力很小——即使是一个健康的妇女,也能毫不费力地向北行走好几浪
 远的路程——不过引力在我们的大部分地区足以充当指南针的角色。此外,雨(每隔一段时间下一次)总是来自北方,这是另一个有利条件。在城镇,我们建有房屋,房屋的围墙大部分当然是朝南北向而建的,屋顶可以挡住来自北方的雨。在没有房屋的乡间,树干充当了向导。总之,我们在确定方位时并没有你所预料的那样困难。
远的路程——不过引力在我们的大部分地区足以充当指南针的角色。此外,雨(每隔一段时间下一次)总是来自北方,这是另一个有利条件。在城镇,我们建有房屋,房屋的围墙大部分当然是朝南北向而建的,屋顶可以挡住来自北方的雨。在没有房屋的乡间,树干充当了向导。总之,我们在确定方位时并没有你所预料的那样困难。
然而,在气候更加温和的地区,南向引力几乎感觉不到,如果我行走在荒原上,没有房屋和树木做向导,我常常被迫在原地静候数小时,直到雨来了,才继续我的旅程。引力对于老弱者,特别是对于柔弱的妇女,要比对强壮的男性重得多,结果,如果你在街上遇见一位小姐,总是把北侧让给她——当你身体健康,且在不易辨别南北的气候里,急切之中做这决定远非一件易事。
我们的房子没有窗户;因为不论屋里屋外,也无论白天黑夜,不论何时何地,光线都同样照射,我们并不知道它来自何处。过去,“光是如何起源的”这个问题对于知识界而言是个十分有趣的且经常研究的问题。不断有人试图解决这个问题,结果,那些“可能的”解决者们都进了疯人院。于是国会立法,对那些研究者征收重税,试图以此来间接地阻止对该问题的研究。现在,我是平面国里唯一一个熟知这个神秘问题答案的人。然而,我不能让我的一个同胞明白我的知识。我是唯一有关空间真理以及光来自三维空间的理论的教授,人们嘲笑我,似乎我是疯子中的最疯者!且不提这个令人丧气的话题,让我回到房屋的话题来吧。
最常见房屋的形状是五边形,如附图(图 1–8)所示。北面的两边 OR 、 OD 构成屋顶,绝大多数房屋在这里没有门。东侧开一小门,供女性出入;西侧开一大门,供大男人们出入。南侧为地板,不设门。
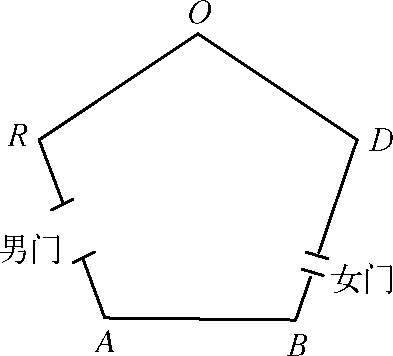
图1—8 平面国的房屋
不允许建正方形和三角形房屋,原因是:正方形和正三角形的角比五边形的角更尖锐,而无生命物体的直线又比人的直线要暗淡,因此,正方形或三角形房屋的尖角会对突然跑向房子的那些粗心大意或心不在焉的行人构成严重伤害。因此,早在 11 世纪,法律就普遍禁止建三角屋,只有堡垒、军火库、兵营以及其他国家建筑物是例外,因为一般公众无须直接走近这些建筑。
这个时期,建正方形房屋仍是处处允许的,尽管国家要征收特别的税。但是,大约三个世纪后,法律规定:在人口超过一万的城镇里,为确保公众安全,最小的屋角必须是五边形的角。国会的努力得到了社会的支持;今天,即使是在乡下,五边形建筑已经取代了其他形状。现在,只有在一些十分偏远落后的农村地区,好古者才能偶然见到一座正方形房屋。
平面国居民的最大长度或宽度大约在 11 英寸左右。12 英寸则是最大值了。
我们的女性是直线。
士兵和最低等的工人阶级是等腰三角形,每条腰大约 11 英寸长。底边很短,常常不超过半英寸,因此顶角十分尖锐、吓人。的确,当底边不到
 英寸时,他们和直线或女性简直无法区分。
英寸时,他们和直线或女性简直无法区分。
中产阶级由等边三角形组成。
专业技术人员、绅士为正方形(我本人即属此类)和正五边形。
再上面是贵族,分好几个层次,最低层次是六边形,其余的边数依次增大,直到拥有正多边形的光荣头衔。最后,当边数变得很大很大,边长变得很小很小,以致整个图形变得与圆无异,他就进阶到圆形或僧侣阶级。这是地位最高的阶级。
我们有一个自然法则,男孩要比父亲增加一边,结果是每一代在地位上都要升一级。正方形的儿子是正五边形,正五边形的儿子是正六边形,依此类推。

图1—9 阿波特

图 1—10 《平面国传奇》书影
但这个法则并不总是适合于商人阶级,对士兵和工人阶级更是不常适用。他们几乎不配具有人类图形的名称,因为他们并非等边。因此,自然法则对它们并不成立;一个等腰三角形的儿子仍然会是等腰三角形。然而,即使对于等腰三角形来说,要让后代最终超出父辈的下层状况,也不是一丝希望也没有。因为在长期的军事胜利、勤奋而娴熟的劳动之后,人们普遍发现,工匠和士兵阶级中那些更聪明者,其底边会微微变长,两腰会微微缩短。下层阶级中这些更聪明的成员,他们的儿女结婚后,所生的下一代一般都会更加接近等边三角形。
在等腰父母的大量等腰子女中,极少是真正的、可以证明的等边三角形。这样的生育结果,不仅需要一系列精心安排的婚姻,而且还需要父母长期不断的节俭、自我克制的训练;还需要经过许多代人耐心的、系统的、持续的发展。
如果哪家等腰父母亲生了一个真正的等边儿子,那么方圆好几浪都会喜气洋洋。经过卫生和社会委员会的仔细检查之后,如果婴儿确属等边,就会举行庄严的仪式,将其接纳为等边阶级。然后他马上会被没有孩子的某个等边族所收养,离开他那自豪却又悲伤的父母。而收养者必须起誓:决不允许孩子再回到原来的家探视双亲,以免刚刚发展好了的机体受不自觉的模仿力的影响,又回到他上一辈的形状。
从奴隶出生的祖辈们的行列中,偶然产生等腰三角形,对于贫穷的奴隶们来说不啻为一束希望之光,因而受到他们的欢迎;同时,这样的事也受到广大贵族们的欢迎,因为所有的高等阶级心里都很清楚:这些罕见的现象对于他们的特权并无什么大碍,却十分有效地阻止了下层民众的革命。
如果下层的锐角民众无一例外、完全失去希望和信心,那么他们的多次暴动中的头领们会十分能干,凭借他们人多力量大,连圆形阶级也拿他们没办法。但自然法则却规定,工人阶级在智慧、知识和一切美德上提高了多少,他们的锐角也会增大多少,并接近无害的等边三角形的角。这样,在最残酷和可怕的士兵阶级——由于缺乏智慧而几乎与女性处于同一层次的人们——中,当运用他们穿透力的智力在增长的同时,他们的穿透力本身却在下降。
多么奇妙的补偿律啊!在平面国中,物竞天择、适者生存以及所谓贵种的神圣起源是多么完美!通过合理运用自然规律,利用人类思想的抑制不住的、无尽的希望,多边形和圆形几乎总是能将暴乱消灭于萌芽状态。艺术也对自然规律助了一臂之力。国家医生所进行的人工浓缩或膨胀手术可以使叛乱领袖变成地道的正三角形,并立刻将他接纳为特权阶级。但更多的仍处于标准之下的人们,由于幻想着有朝一日升为贵人,被吸引进国家医院,他们在那里会受到体面的监禁。一两个固执、愚蠢、不规则得无药可救的人则被处以极刑。
这样,可怜的等腰下层民众变得群龙无首,他们那些被圆形阶级雇为专门对付暴乱事件的少数兄弟们把他们愚弄得麻木不仁、毫无斗志。圆形阶级还在他们之间巧妙地制造妒忌、猜疑,挑起他们之间的战争,彼此用尖角杀死对方。每年发生不少于120 次的叛乱,此外还有 235 次小规模的起义;但他们都遭到同样的下场。
一天,主人公不幸被一个来自三维空间世界的球体所覆盖——在平面国的人看来,球当然只是一个圆,先从一个点开始逐渐增大,而后又逐渐减小,最后消失。球体降落多次,它向正方形描述了三维世界的奇迹,并使他意识到自己被限制在平面上的不幸境况。最后,这位陌生人将正方形带去环游三维空间。回国后,他热衷于向国人传授自己刚刚发现的三维空间理论:
尽管向孙子传授三维理论的尝试失败了,但这并没有让我丧失向家中其他成员传授该理论的信心。只是我想明白了:我不该完全依靠太引人注目的字眼——“向上,而非向北”,而必须让公众对整个理论有一个清晰的了解;为此,似乎需要借助于文字才行。
于是,我花了数月时间写了一本关于三维空间秘密的小册子,为了避免法律的制裁,我在书中并没有直言现实世界的维度(physical dimension),而只是塑造了一个想象中的世界,在那里,一个人可以从上往下看平面国,他能同时看到所有事物的内部,并且在那里,似乎存在一个由 6 个正方形所围成的、包含 8 个顶点的图形。但是,在写这本书时,我很痛苦地发现,我无法画出这个图形;因为,在我们的平面国里,除了直线以外,并没有其他书板,除了直线以外并没有其他图形;一切都在同一直线上,只有通过大小和亮度才能加以区分。结果,当我写完小册子(我取名为《从平面国到理想国》),我丝毫没有把握,是否会有人能明白我的意思。
与此同时,我的生活开始笼罩在阴云之中,毫无乐趣可言。我所见到的一切都诱使我公然叛逆。因为我只能将我在二维所见的事物与在三维世界所见的真实面目相比较,且几乎无法克制自己大声说出这样的比较。我把当事人及自己的事抛诸脑后,整天陷于对我曾经见到的却又无法传授给任何人、即使在我自己的头脑中也日益难于复制的秘密的沉思默想之中,不能自拔。
我从空间世界回来大约 11 个月之后的一天,我闭着眼睛,试图回想起正方体的形状,但想不出来;尽管后来终于想出,但并没有把握是不是它的原貌。这使我比以前更加犹豫,并使我下决心采取某种措施。但采取什么样的措施呢?我不知道。我感到自己将心甘情愿把一生献给事业,如果我因此可以让人们相信我的理论的话。但是,如果我连自己的孙子都说服不了,又怎能去说服这块土地上的最高级、最发达的圆形阶级呢?
我的情绪常常变得过于强烈,我常常忍不住说出一些危险的话来。我已经被看作是异端,如果不是叛逆的话。我已危机四伏。但我又常常不能克制自己,大声说一些怀疑的、半带煽动性的话,即使是在最高等级的多边形和圆形阶级面前也毫不忌讳。例如,一些疯子自称具有能够看清事物内部的特异功能,针对如何对它们进行治疗的问题,我会引述古代一位圆形的话说,预言家和富有灵感的人总是被大多数人看作疯子;有时我抑制不住要吐出诸如“看透事物内部的眼睛”以及“能看见一切的世界”之类的话。有一两次,我甚至口不择言地说出“三维和四维”这样的禁用语。有一次,在长官本人的官邸举行的地方思索协会会议上,某个愚蠢至极的人物宣读了长篇论文,说明为什么上帝会把维数限制在2以及为什么只有上帝才具有看穿一切的能力的“真正原因”。当时,我忘乎所以,详细叙述了自己如何随球体到空间世界环游,又如何回家的经过以及耳闻目睹的每一件事。一开始,我还假装是在描述一个虚构人物的想象中的经历;但那时我热血沸腾、激动万分,一时毫无顾忌地实话实说、露出真相。在演说的最后,我奉劝所有的听众抛开偏见,相信三维理论。
不用说,我立即被逮捕,并被送交议会处置。
翌日晨,就在数月前球体和我一起站立过的地方,我被允许继续讲述我的经历,没有质疑,不被打断。但一开始我就预感凶多吉少;因为在我开始辩护之前,总统命令由 2 ° 或 3 ° 的低等警察来换走 55 ° 左右的高等警察。我心里很清楚那意味着什么。我将被处以极刑或被投入大牢,那些听到我的故事的官员们也将同时被处死,这样,这个世界上就再也无人知道我的故事了。为此,总统希望用更廉价的牺牲品来代替昂贵的牺牲品。
在我辩护完毕之后,总统或许看到有些低层次的圆形们为我的真诚所感动,便问我如下两个问题:
一、当我使用“向上,而非向北”这句话时,我能不能将所说的方向具体指出来?
二、我能否利用图形或描述(而不是列举想象的边和角)来说明我喜欢称之为正方体的图形?
但我声明,我再也不能说什么了,我必须将自己交给真理,它的事业最终必将盛行于世。
总统回答说:他对我深表同情,我做得再好不过了。必须判我终身监禁,但如果真理打算让我出狱向世界传播福音,真理将被授权这样做。同时,我还有越狱的机会。并且,除非我因为犯错误,而被剥夺特权,否则偶尔可以允许我和我的兄弟见面,他在我之前进了监狱。
光阴荏苒、岁月如梭。一晃七年过去了。而我仍然是个阶下囚。除了偶尔见见我的兄弟外,我不能见狱友之外的任何人。我的兄弟是最好的正方形之一,正直、聪明、乐观、与我手足情深。但我必须承认,每周的见面都让我痛心疾首。当球体在议院现身的时候,他也在场;他看见球的截面在改变,他听到我对这现象向圆形们所做的解释。从此,整整 7 个年头里,每周他都会看我重复在球体现身时我所扮演的角色,详细叙述空间世界所有的现象,以及通过类比导出的立体事物的存在性。但是,我不得不承认,我的兄弟并没有理解三维的本质,他坦言自己并不相信球体的存在。
因此,我是绝对没有信徒的。千年启示录又有什么用呢?空间世界中的普罗米修斯因为给人间带去火种而受桎梏,而我呢?我这个平面国的普罗米修斯身陷囹圄,却什么也没有带给国人。但我心存希望:这些记录能以某种方式让某个维数的人类所了解,并激起那些拒绝限制在一个有限维度里的人们的反叛。
那是我在快乐时刻的希望。但并不总是这样。一想到我不能如实说出我对曾经见到过的立方体的准确形状感到有把握,我就仿佛被压得喘不过气来。在模糊的梦幻中,神秘的箴言“向上,而非向北”就像吞噬灵魂的斯芬克斯一样,萦绕在我的心间。当正方体和球体悄然飞入不可能存在的背景中去时;当三维土地几乎和一维世界或零维世界一样虚幻时;甚至当这堵让我失去自由的高墙、我正在写字的这些书板,以及平面国自身所有的现实都与病态想象的产物或毫无根据编织出来的梦一样糟糕时,精神脆弱的时节来临了。这正是我为了真理而不得不忍受的苦痛!
《平面国传奇》利用数学主题对维多利亚时代的社会等级制度和性别歧视以及人类的狭隘和墨守成规作了辛辣的讽刺和批判。
在18 世纪杰出讽刺小说家斯威夫特(J. Swift, 1667—1745)的《格列佛游记》中,也有许多数学例子。在第一卷中,利立浦特人利用立体图形的相似性来确定“我”的体积和饭量
 :
:
皇帝规定每天供给我足够维持一千七百二十八个利立浦特人的肉类和饮料。以后不久我问在朝廷做官的一位朋友,他们怎样得出这样一个确定的数目。他告诉我,御用数学家用四分仪测定了我的身长,计算出我的身长和他们的比例是十二比一,由于他们的身体和我完全一样,因此得出结论:我的身体至少抵得上一千七百二十八个利立浦特人。我所需要的食物数量足够供给这么多的利立浦特人。
同书第三卷中提到,勒皮他的仆人们把面包切成圆锥体、圆柱体、平行四边形和其他几何图形;勒皮他人的思想永远跟线和圆相联系,他们赞美女性,总爱使用菱形、圆、平行四边形、椭圆以及其他几何术语。这里,作者的图形分类不甚合理。
科幻小说之父凡尔纳(J. Verne, 1828—1905)在《神秘岛》中巧妙地使用了等比数列
 。当哈伯在衣服夹层里找到一颗麦粒时,工程师史密斯如是说:“如果我们种下这粒麦子,那么第一次我们将收获八百粒麦子;种下这八百粒麦子,第二次将收获六十四万粒;第三次是五亿一千二百万粒;第四次将是四千多亿了。比例就是这样……这就是大自然繁殖力的算术级数……算他十三万粒一斗,就是三百万斗以上。”这里,作者误将几何级数说成算术级数。
。当哈伯在衣服夹层里找到一颗麦粒时,工程师史密斯如是说:“如果我们种下这粒麦子,那么第一次我们将收获八百粒麦子;种下这八百粒麦子,第二次将收获六十四万粒;第三次是五亿一千二百万粒;第四次将是四千多亿了。比例就是这样……这就是大自然繁殖力的算术级数……算他十三万粒一斗,就是三百万斗以上。”这里,作者误将几何级数说成算术级数。
在19 世纪的欧洲和俄国,数学与更严肃的文学也发生了联系。俄国大文豪陀思妥耶夫斯基(F. Dostoevsky,1821—1881)在其长篇小说《卡拉马佐夫兄弟》第 2 部第 2 卷第 3 节“兄弟俩互相了解”中,伊凡和阿辽沙兄弟俩在一家酒店喝茶聊天。在谈到上帝是否存在的问题时,伊凡说:

图 1—11 陀思妥耶夫斯基(苏联,1971)
假如上帝存在,而且的确是他创造了大地,那么我们完全知道,他也是照欧几里得的几何学创造大地和只有三维空间概念的人类头脑的。但是以前有过,甚至现在也还有一些几何学家和哲学家,而且还是最出色的,他们怀疑整个宇宙,说得更大一些——整个存在,是否真的只是照欧几里得的几何学创造的。他们甚至还敢幻想:按欧几里得的原理是无论如何也不会在地上相交的两条平行线,也许可以在无穷远的什么地方相交。因此我决定,亲爱的,既然我连这一点都不能理解,叫我怎么能理解上帝呢? [8]
这里,非欧几何的观念成了挑战传统上帝信仰的有力工具。
在奥地利著名小说家穆西尔(R. Musil, 1880—1942)出版于 1906年的小说《小特尔莱斯》里,主人公特尔莱斯在学习虚数概念后,和他的同学有下面一段对话
 :
:
“我说,你真的理解所有那些内容了吗?”
“什么内容?”
“所有关于虚数的内容。”
“是的,这并不是特别难,是吗?你要做的只是记住–1 的平方根是你使用的基本单位。”
“但问题就在这里。我的意思是说,根本没有这样的事。每一个数,无论正还是负,其平方都是正数。所以不可能有任何一个实数会是负数的平方根。”
“没错。但我们为什么不可以用完全一样的方式来计算负数的平方根呢?这当然不可能产生任何实数,正因为如此,我们把结果称为虚数。这就像有个人过去总是坐在这儿,所以我们今天仍为他放张椅子在这里,即使这个时候他死了,我们仍当作他要来一样,继续做这件事。”
“但是,当你确信无疑地(像数学那样确定)知道这不可能时,你怎么还会这么做呢?”

图1—12 穆西尔

图 1—13 电影《小特尔莱斯》
“无论如何,你继续去做,就好像并非如此一样。它可能会产生某种结果。毕竟,这与无理数——永远除不尽,无论你花费多长时间算下去,永远永远永远都不可能得到其分数部分最后的值——不同在何处呢?你怎能想象平行线会在无穷远处相交?在我看来,如果我们过于谨小慎微,那么数学就根本不存在了。”
特尔莱斯遇到虚数后,开始考虑生命的复杂性和模糊性。特尔莱斯原来把数学看作“生命的预备工具”,因此为虚数所困扰。他认为,虚数不可能是一个真正的数;但同时,通过虚数运算所得到的真实结果又把他给迷住了。他承认,这样的运算使他感到有点“晕乎乎”,似乎是通往“上帝所知道的路”。对特尔莱斯而言,实数和虚数代表着人性中理性的一面和非理性的一面。
俄国小说家扎米亚金(Y. Zamyatin, 1884—1937)也借虚数概念来宣扬人类信仰、情感等所具有的非理性的一面。在反乌托邦小说《我们》(1924)中,扎米亚金虚构了一个用数学来管理的极权国家——一统国。在这个国家,统治者是“万数之数”;诗歌是严格按照乘法表来写的;人名是用数字来表示的。《我们》中的故事是围绕一位国家数学家、“积分号”宇宙飞船的设计者D-503 展开的。当D-503 与一位反政府的女革命者I-330 产生爱情后,他的理性受到了挑战。早在遇见I-330 以前,D-503 就已经发觉虚数“奇怪、陌生、可怕”,他痛恨这种数,希望这种数不存在。遇见I-330 之后,虚数成了D-503 情感与理智紊乱以及他无视国家法规的象征。D-503 被诊断为“有灵魂和想象力”,最后被新发明的算法切除,D-503 也因此恢复了国家数学家的地位。
在《我们》中,D-503 试图解释一统国中人们是如何量化幸福(happiness)的。他建立了一个公式
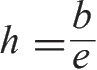 ,其中
b
表示快乐(bliss),
e
表示嫉妒(envy)。这个公式表明:一个人若要幸福,并不需要他有多少快乐,而只要快乐大于嫉妒即可。即使他境况不佳,如
b
= 0.001,但如果嫉妒远小于快乐,如
e
= 0.000001,那么,根据幸福指数公式,
h
= 1000,此人应该很幸福!不知D-503 所给幸福公式是否也适用于我们这个物欲横流的世界?
,其中
b
表示快乐(bliss),
e
表示嫉妒(envy)。这个公式表明:一个人若要幸福,并不需要他有多少快乐,而只要快乐大于嫉妒即可。即使他境况不佳,如
b
= 0.001,但如果嫉妒远小于快乐,如
e
= 0.000001,那么,根据幸福指数公式,
h
= 1000,此人应该很幸福!不知D-503 所给幸福公式是否也适用于我们这个物欲横流的世界?

图 1—14 扎米亚金

图 1—15 《我们》扉页
当然,除了非欧几何、虚数等概念外,作家也借助更传统的数学概念来刻画他的故事情节。安德烈·贝里(Andrei Bely, 1880—1934)出版于 1916年的《彼得堡》( Petersberg )一书采用的基本图式是一个球体。书中,直线、多边形、立方体代表规则和稳定,而加宽的圆和扩展的球则代表了“崩溃和死亡”。政府官员阿波罗诺维奇(Apollonovich)看到一排排立方体形状的房子就感到特别舒服,他酷爱“直线的景观”。但是,当他的儿子尼科莱(Nikolai)良心发现,不想谋杀自己的父亲之后,父子俩被一系列令人不安的东西所包围,这些东西都呈现恐怖的球体,包括阿波罗诺维奇死去的心以及尼科莱那些激进的同伴们提供给他的弒父凶器——装在一个球形沙丁鱼罐头里、用来在膨胀的球体内爆炸的定时炸弹。

图1—16 安德烈·贝里
俄国大作家列夫·托尔斯泰(Leo Tolstoy, 1828—1910)在《战争与和平》中利用数学来支持自己的历史理论。托尔斯泰利用古希腊著名的芝诺悖论——阿喀琉斯追不上乌龟来说明:历史是不能够作为一系列离散的片段来分析的,历史不是离散的事件,而是一个连续的过程,是无穷小量(“历史的微分”)的和(“积分”)。只有找到求和的方法,人们才有望认识历史的法则。

图1—17 托尔斯泰(苏联,1960)
托尔斯泰还试图用比率和方程来说明:除了数量,士气也是一个军队获胜的重要因素,士气乘上数量就等于力量。一支小的部队如果士气高,也能够打败大的部队。他举例说(以 X 和 Y 表示士气):
10 个人,10 个营,或 10 个师,同 15 人,15 个营,或 15 个师作战,把 15 个那一方打败了,也就是说,把对方一个不剩地全部打死,或俘虏了,而自己损失了 4 个人,这就是说,一方损失了 4 个,另一方损失了 15 个。这样一来 4 个就等于 15 个,这就是说 4
X
= 15
Y
。因而
X
∶
Y
= 15 ∶ 4,这个方程式并未告诉我们那个未知数的值,但是告诉了我们那两个未知数的比率。可以取各种各样的历史单位(战斗、战役、战争阶段)列成这种方程式,得出许多系列数字,在那些数字里,应当存在一些法则,是可以发现的。

数学也是作家刻画人物聪明才智的一种工具。我国当代武侠小说家金庸(1924—2018)在《射雕英雄传》第 29 回和 31 回中通过宋元时期的数学问题(开方、幻方、天元术、四元术、同余问题等)来刻画才智过人的黄蓉形象。以下是第 29 回“黑沼隐女”片段:
黄蓉坐了片刻,精神稍复,见地下那些竹片都是长约四寸,阔约二分,知是计数用的算子。再看那些算子排成商、实、法、借算四行,暗点算子数目,知她正在计算五万五千二百二十五的平方根,这时“商”位上已记算到二百三十,但见那老妇拨弄算子,正待算那第三位数字。黄蓉脱口道:“五!二百三十五!”那老妇吃了一惊,抬起头来,一双眸子精光闪闪,向黄蓉怒目而视,随即又低头拨弄算子。这一抬头,郭、黄二人见她容色清丽,不过四十左右年纪,想是思虑过度,是以鬓边早见华发。那女子搬弄了一会,果然算出是“五”,抬头又向黄蓉望了一眼,脸上惊讶的神色迅即消去,又见怒容,似乎是说:“原来是个小姑娘。你不过凑巧猜中,何足为奇?别在这里打扰我的正事。”顺手将“二百三十五”五字记在纸上,又计下一道算题。这次是求三千四百零一万二千二百二十四的立方根,她刚将算子排为商、实、方法、廉法、隅、下法六行,算到一个“三”,黄蓉轻轻道:“三百二十四。”那女子“哼”了一声,哪里肯信?布算良久,约一盏茶时分,方始算出,果然是三百二十四。那女子伸腰站起,但见她额头满布皱纹,面颊却如凝脂,一张脸以眼为界,上半老,下半少,却似相差了二十多岁年纪。她双目直瞪黄蓉,忽然手指内室,说道:“跟我来。”拿起一盏油灯,走了进去。郭靖扶着黄蓉跟着过去,只见那内室墙壁围成圆形,地下满铺细沙,沙上画着许多横直符号和圆圈,又写着些“太”“天元”“地元”“人元”“物元”等字。郭靖看得不知所云,生怕落足踏坏了沙上符字,站在门口,不敢入内。黄蓉自幼受父亲教导,颇精历数之术,见到地下符字,知道尽是些术数中的难题,那是算经中的“天元之术”,虽然甚是繁复,但只要一明其法,也无甚难处。

图1—18 1983 年版电视剧《射雕英雄传》
黄蓉从腰间抽出竹棒,倚在郭靖身上,随想随在沙上书写,片刻之间,将沙上所列的七八道算题尽数解开。这些算题那女子苦思数月,未得其解,至此不由得惊讶异常,呆了半晌,忽问:“你是人吗?”黄蓉微微一笑,道:“天元四元之术,何足道哉?算经中共有一十九元,‘人’之上是仙、明、霄、汉、垒、层、高、上、天,‘人’之下是地、下、低、减、落、逝、泉、暗、鬼。算到第十九元,方才有点不易罢啦!”那女子沮丧失色,身子摇了几摇,突然一跤跌在细沙之中,双手捧头,苦苦思索,过了一会,忽然抬起头来,脸有喜色,道:“你的算法自然精我百倍,可是我问你:将一至九这九个数字排成三列,不论纵横斜角,每三字相加都是十五,如何排法?”黄蓉心想:“我爹爹经营桃花岛,五行生克之变,何等精奥?这九宫之法是桃花岛阵图的根基,岂有不知之理?”当下低声诵道:“九宫之义,法以灵龟,二四为肩,六八为足,左三右七,戴九履一,五居中央。”边说边画,在沙上画了一个九宫之图。那女子面如死灰,叹道:“只道这是我独创的秘法,原来早有歌诀传世。”黄蓉笑道:“不但九宫,即使四四图,五五图,以至百子图,亦不足为奇。就说四四图罢,以
十六字依次作四行排列,先以四角对换,一换十六,四换十三,后以内四角对换,六换十一,七换十。这般横直上下斜角相加,皆是三十四。”那女子依法而画,果然丝毫不错……
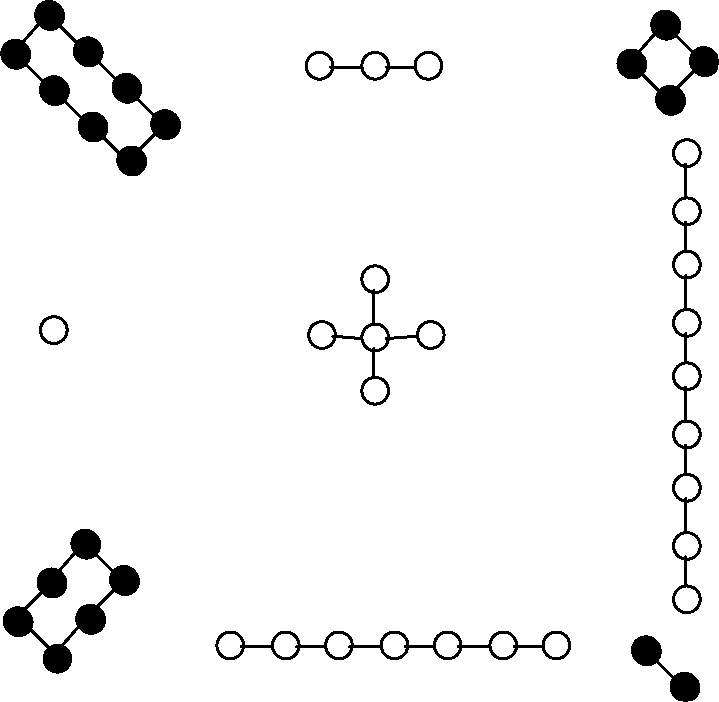
图1—19 中国古代的洛书(九宫图)
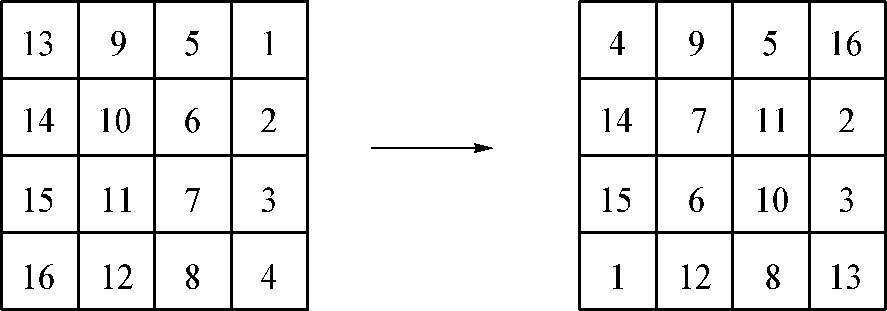
图 1—20 南宋杨辉四四图的构造
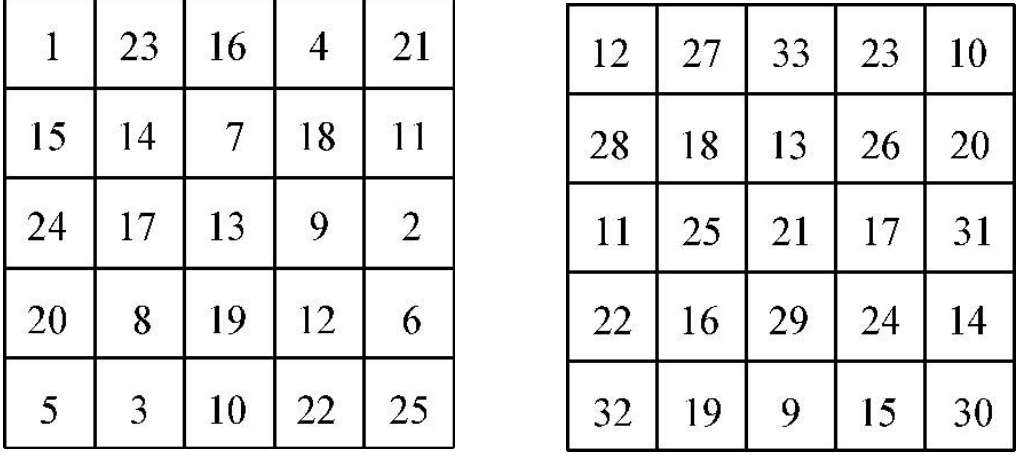
图 1—21 杨辉的五五图
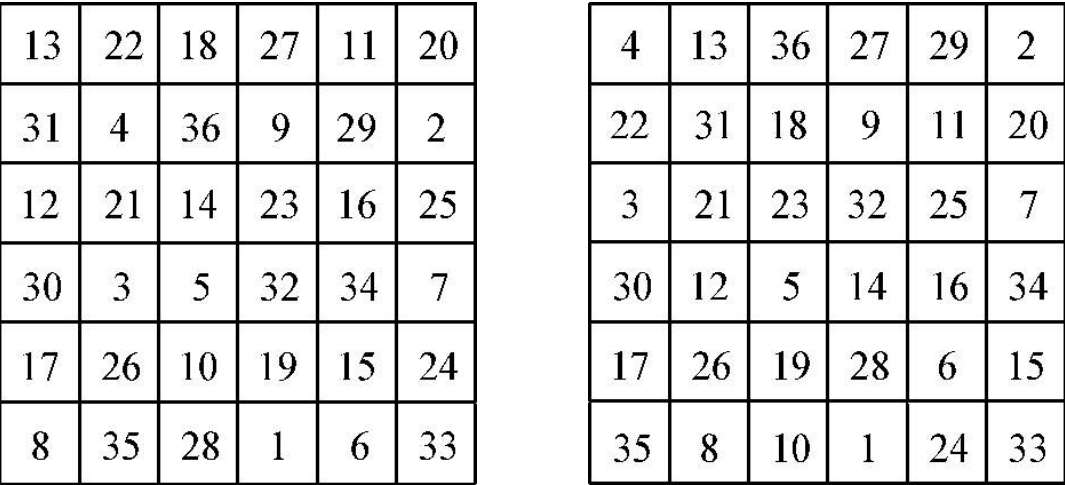
图 1—22 杨辉的六六图
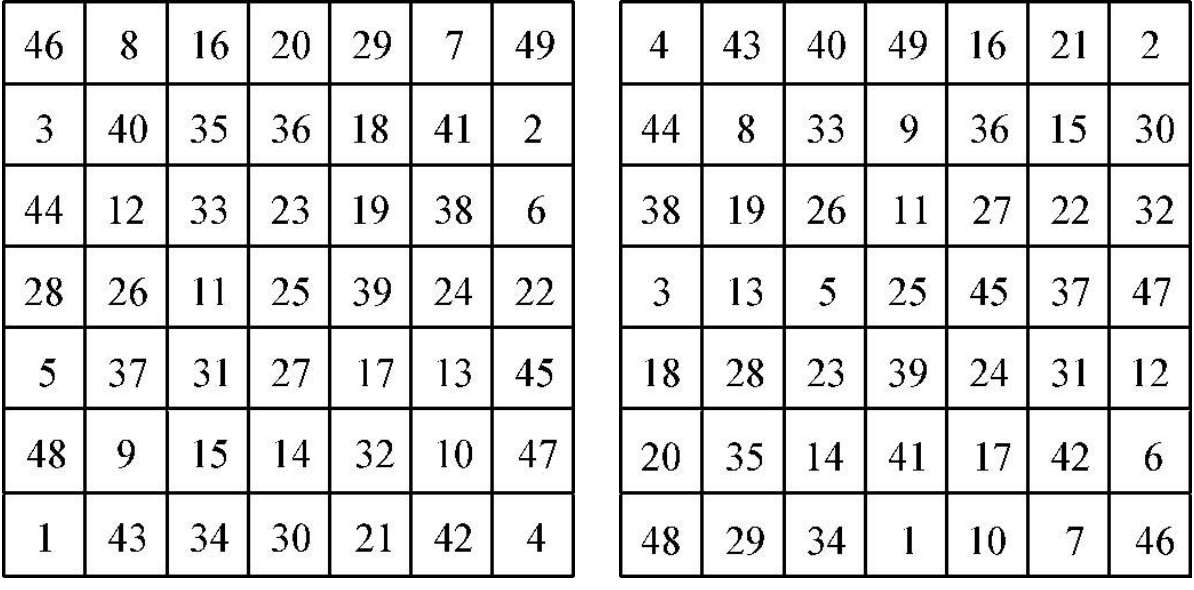
图 1 -23 杨辉的七七图(衍数图)
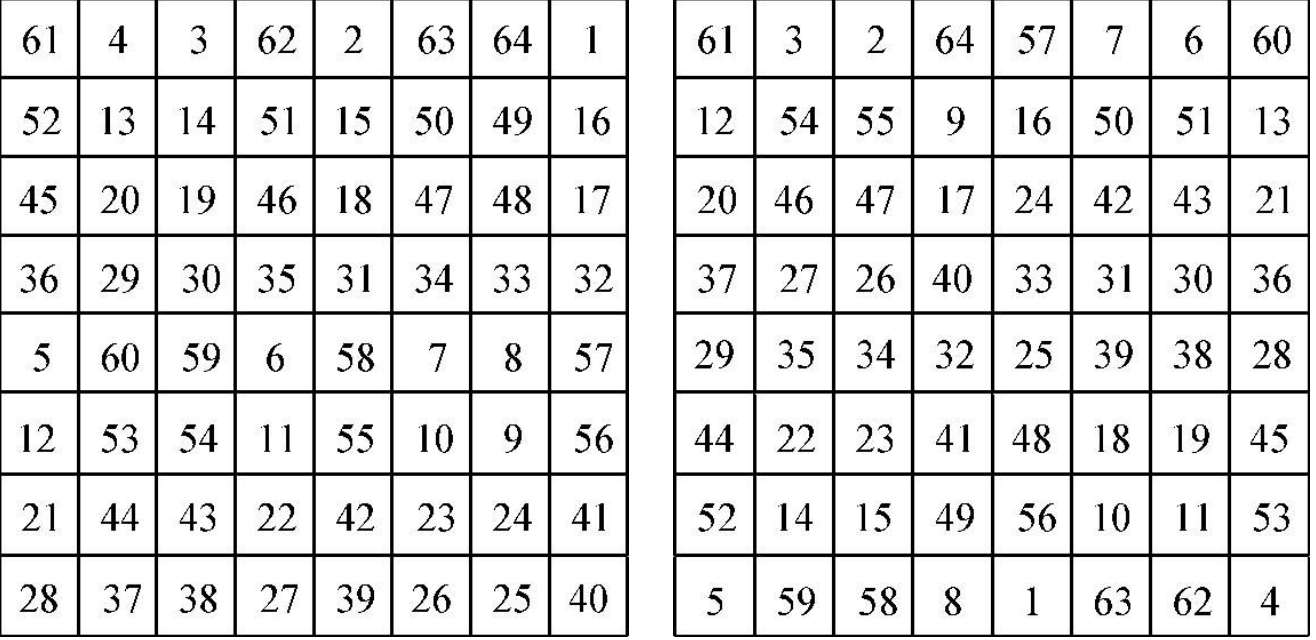
图 1—24 杨辉的六十四图(易数图)
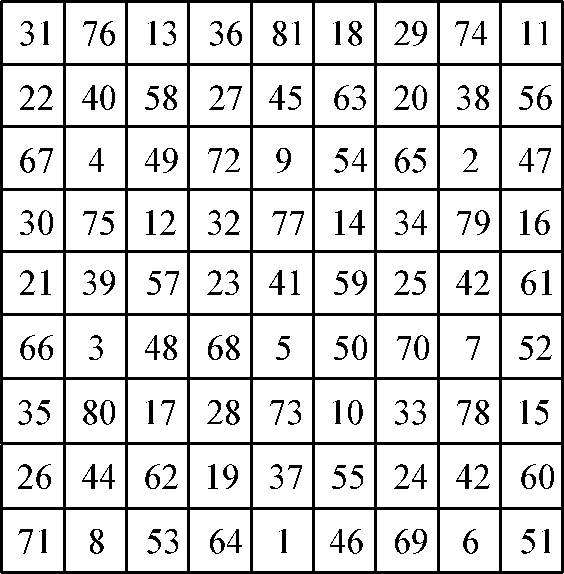
图 1—25 杨辉的九九图
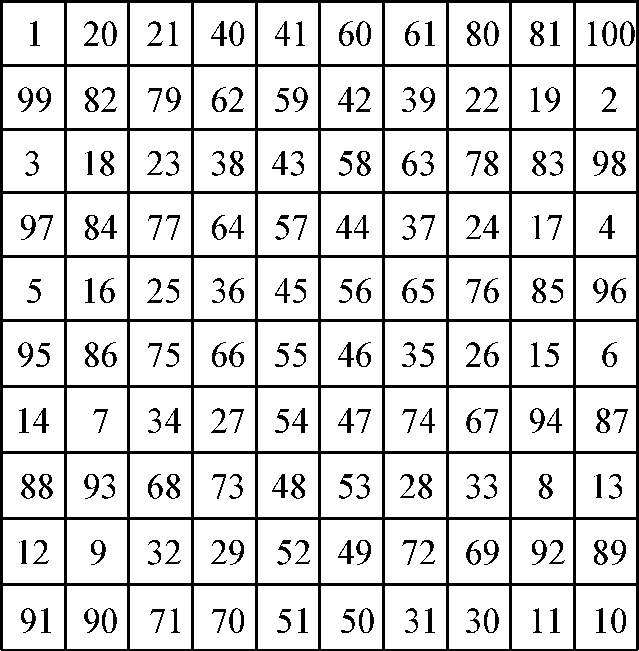
图 1—26 杨辉的百子图
著名作家王蒙是数学的爱好者,他说:“回想童年时代花的时间一大部分用在做数学题上,这些数学知识此后直接用到的很少,但是数学的学习对于我的思维的训练却是极其有益的。”在《我的人生哲学》中,作者多次通过数学概念来思考人生
 :
:
与无限长远的永恒与无限辽阔的宇宙相比较,人类特别是人类个体就渺小得可以不计了。是的,当分母是无限大的时候,与之相比的人也好蚁也好菌也好,或者地球也好太阳系也好一个与几个银河系也好,蜉蝣之一进一夕也好,人之不满百年也好,古柏之五千岁也好,都是同样地几乎没有区别地趋向于零,趋向于可以略而不计。从这个意义上来说,也许论述人生的无意义有它的合理的一面,也许论述时间与空间的无限与人生的短促有助于使人的心胸开阔气象宏大,也许这种念天地之悠悠独怆然而涕下的心绪带几分终极眷顾的宗教色彩。

图 1—27 “无穷大”符号(阿根廷,2000)
一个线段,最美的分割是使之做到全线段与大线段的比,等于大线段与小线段的比,这又叫做内外比。设大线段为 a ,小线段为 b ,则 a + b : a = a : b 。如果全线段为十分,那么大线段应是 6.18 分,而小线段为 3.82 分。设你的能力是 10 分,你得到了3.82 分的评价或回报,足可以了。你做出的成绩实绩,应该力争不少于 6.18 分,而你的学习你的投入你的奋斗精神,应该只是多于而绝对不是少于 10 分,符合这个黄金分割的比例,你的形象是美丽的。如果你的获得超过了 38.2%,你有可能被认定为一个侥幸者投机者早晚要跌下来者,春风得意于一时,不等于春风得意于永久。
有一个骗人的游戏,我是在北戴河海滨第一次看到的。经营游戏者放四种不同颜色的玻璃球在口袋里,每种颜色的球都是 5个,然后让人从口袋里摸 10 个球,并规定了不同出球的比例下的不同的奖惩方法。他的规定是摸出来的球是 3322 比例的(即A、B两种颜色的球为三,C、D两种颜色的球为二,或A、C三,B、D二或其他),玩者要罚款 5 元;如果摸出来是 4321 或 3331,玩者罚 2 元;如果摸出来是 4222,为五等奖,奖励一个小海螺或一个钥匙链之类;如果是 4330 或者 4411,为四等奖,奖励一盒进口香烟;如果是 5311,为三等奖,奖励一个机器人玩具;如果是5410,为二等奖,奖励一条进口香烟;而如果是 5500,为大奖,奖励一台摄像机。
表面看来,似乎是得奖的机会多于受罚的机会,而且是免费参加摸奖,只缴罚金,不用“入场券”。于是许多人上当来玩儿这个所谓“免费游戏”。然而我冷眼旁观,十之八九摸出来的都是3322,十分之一二摸出来的是 4321 或 4330,偶然的有人摸出4222 或 4411 或 4330。至于摸到点 5500 的从未一见。摸不着奖反而受罚的人大骂自己的手臭,乐坏了设局者。我回家后用扑克牌或麻将牌也试过,同样是十之八九是 3322,十之一二是 4321 或4330(参阅问题研究[6–9])。
就是说,一切机会趋向于均等,不是你 3,就是我 2,不是你4(已经少见),就是我 3,独占两个 5 的可能几乎近于零,独占一个 5 的事也很难发生。我称之为命运的数学意义上的公正性。这是一个丝毫也不复杂的几率问题,数学家当可为之列出公式。
与此同时,机会又有一种参差性、不相同性、偶然性。如果你放的不是 20 个球而是 24 个球,如果你要的不是 3322 而是3333,你反而得不到成功。3 与 2 是一重参差,一重相互有别,球的颜色又是各自不同,各次不同,形成第二重参差。假设四种球的颜色分别为红黄蓝白,红 3 蓝 3,黄 2 白 2 是 3322,红 3 黄 3蓝 2 白 2 也是 3322,然后是红白蓝黄、白黄红蓝、白蓝红黄等也都可排成 3322,既相同相对公正又不同,变化多端,参差有致,难以琢磨。呜呼,数学之道,大矣!
从中我思索了良久,我想这就是命运,这就是机会,这就是冥冥中的一只手。对于无神论者,命运是数学的公式和规律,数学就是上帝就是主。你想占有一切好运,或者你埋怨一切霉头都降临于你,这就与声称自己总是得到 5500 一样,不是完全不可能,但机会极少,几率极低。真得到这种点数,就像买彩票中了特等奖,就像坐飞机碰到了空难,谁也挡不住,谁都得认命。想明白了这一点,我们可以少一点怨天尤人。
意大利新锐作家保罗·乔尔达诺(Paolo Giordano)在《质数的孤独》中,塑造了一对少年时代各自遭遇不幸的男女主角的爱情故事。男主角叫马蒂亚,女主角叫爱丽丝,他们就像一对孪生质数,彼此相爱,却从未能走到一起
 。
。
质数只能被一和它自身整除。在自然数的无穷序列中,它们处于自己的位置上,和其他所有数字一样,被前后两个数字挤着,但它们彼此间的距离却比其他数字更远一步。它们是多疑而又孤独的数字,正是由于这一点,马蒂亚觉得它们非常奇妙。有时候他会认为,它们是误入这个序列中的,就像是串在一条项链上的小珍珠一样被禁锢在那里。有时候他也会怀疑,也许它们希望像其他所有数字一样普普通通,只是出于某种原因无法如愿。这后一种想法经常在晚间光顾他的大脑,夹杂在睡梦前凌乱而交错的各种形象之中,这个时候,他的大脑会非常疲顿,不愿再编制谎言。
在大学一年级的一门课上,马蒂亚知道,在质数当中还有一些更加特别的成员,数学家称之为“孪生质数”,它们是离得很近的一对质数,几乎是彼此相邻。在它们之间只有一个偶数,阻隔了它们真正的亲密接触,比如十一和十三,十七和十九、四十一和四十三。假如你有耐心继续数下去,就会发现这样的孪生质数会越来越难遇到,越来越常遇到的是那些孤独的质数,它们迷失在那个纯粹由数字组成的寂静而又富于节奏的空间中。此时,你会不安地预感到,到那里为止,那些孪生质数的出现只是一种偶然,而孤独才注定是它们真正的宿命。然后,当你正准备放弃的时候,却又能遇到一对彼此紧紧相邻的孪生质数。因此,数学家们有一个共同的信念,那就是要尽可能地数下去,早晚会遇到一对孪生质数,虽然没人知道它们会在哪里出现,但迟早会被发现。
马蒂亚认为他和爱丽丝就是这样一对孪生质数,孤独而失落,虽然接近,但却不能真正触到对方……
这里,作者借数论中的“孪生质数”概念,刻画了两个主人公之间的关系。一方面,在自然数序列中,质数的分布越往后越稀疏,这象征着男女主人公在现实世界的茫茫人海中是孤独而失落的个体;另一方面,孪生质数中间隔了一个偶数,它们彼此靠近,却不能真正毗邻,这象征着孤寂的男女主角,心灵相通,成了彼此的慰藉,却未能走到一起,白头偕老。这让我们想起了马弗尔平行线般的爱情(参阅第57 页)。
[1] Heath T L. A History of Greek Mathematics . London: Oxford University Press, 1921:220–221.
[2] Heath T L. A History of Greek Mathematics . London: Oxford University Press, 1921: 245.
[3] Pycior H M. Mathematics and prose literature. In: Grattan-Guinness I (ed.). Companion Encyclopedia of the History and Philosophy of Mathematical Sciences (Vol.I), Lodon:Routledge, 1994.
[4] Buchanan S. Poetry and Mathematics . Philadelphia: J. B. Lippincott Company, 1962.
[5] Watkins J J. Review of Lewis Carroll in Numberland: His Fantastical Mathematical Logical Life. Mathematical Intelligencer , 2009, 31(4): 60–62.
[6] Wilson R. Lewis Carroll in Numberl and: His Fantastical Mathematical Logical Life . New York: W. W. Norton & Company, 2008: 149–170.
[7] Newman J R (ed.). The World of Mathematics (Vol. 4). New York: Simon and Schuster,1956: 2383–2396.
[8] Dostoevsky F. The Brothers Karamazov. Translated by Garnett C. http://www. ccel.org/ d/dostoevsky/ karamazov/ karamazov. html.