下载掌阅APP，畅读海量书库
立即打开
亚伯拉罕·棣莫弗是一名来自法国的新教徒，曾在家乡维特里遭受天主教当局的迫害，被监禁两年后才得以出逃。
1688年，21岁的棣莫弗来到了伦敦，一边拜读牛顿的著作、学习各种数学知识，一边当家教谋生。最终，他成功地将伯努利的理论向前推进了一步。
前面我们曾提到，帕斯卡和费马研究了赌局被迫终止的情况下，赌资该如何公平分配的问题。他们的结论是，我们应当考虑如果比赛继续进行，两个人获胜的概率分别有多大。换句话说，我们需要分析剩下的所有可能发生的结果中，哪些会令 A 获胜，哪些会令 B 获胜。
他们讨论的其实就是本小节要介绍的二项分布。如果你抛一枚硬币，那它要么正面朝上，要么背面朝上。如果你将一枚硬币抛两次，那么结果只有正正、反反、正反、反正4种。两次正面、两次反面的情形都只有一种，但一正一反的情形有2种。列成表格就是：
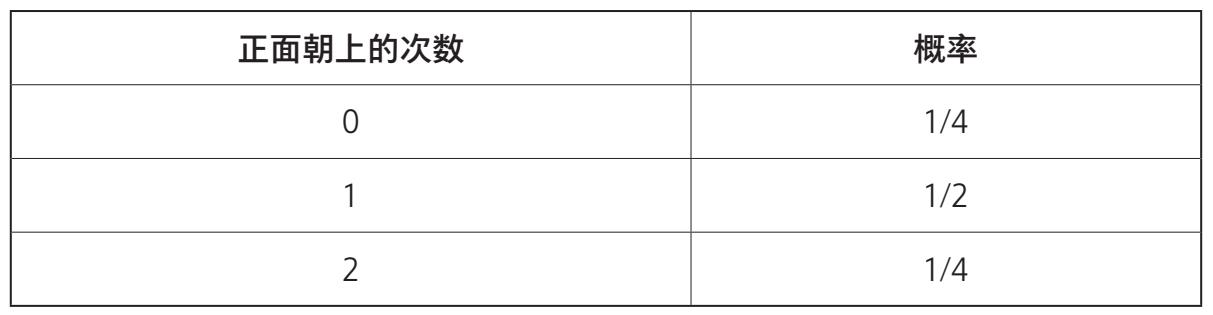
当然你也可以把它画成数据图：
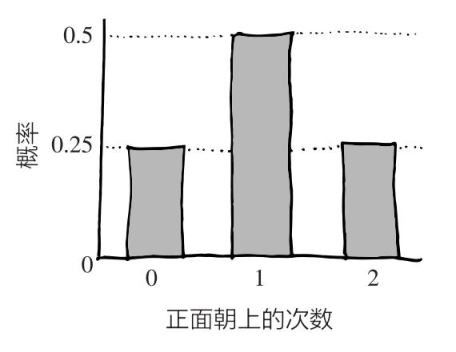
这就是连抛2次硬币的概率分布（只要是“每次只会出现两种结果，且概率相等”的事件，其概率分布就是这样）。连抛4次硬币的概率分布表如下：
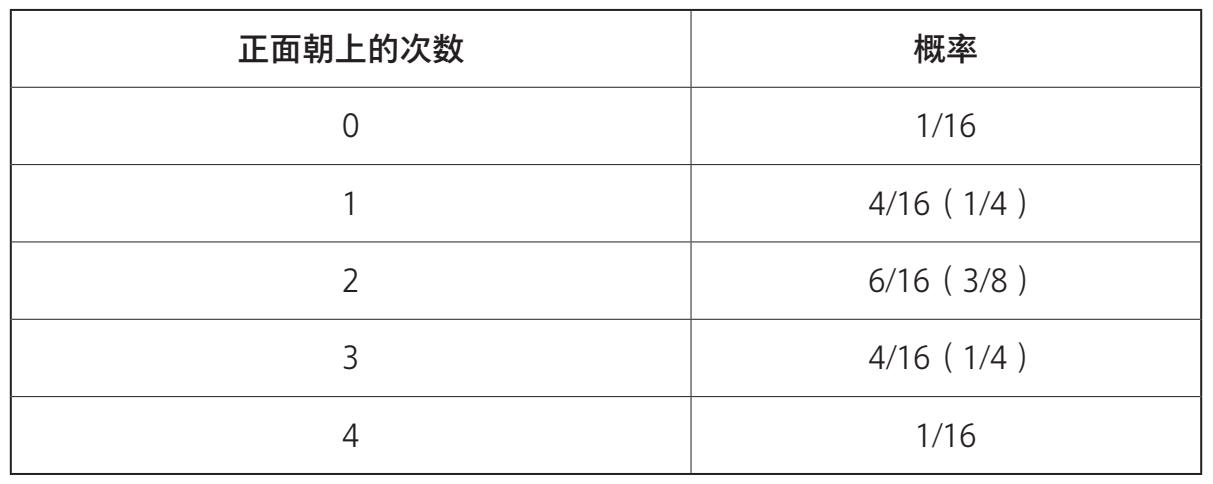
（你应该已经发现了，分子就是杨辉三角形第4行的数字）画成概率分布图就是：
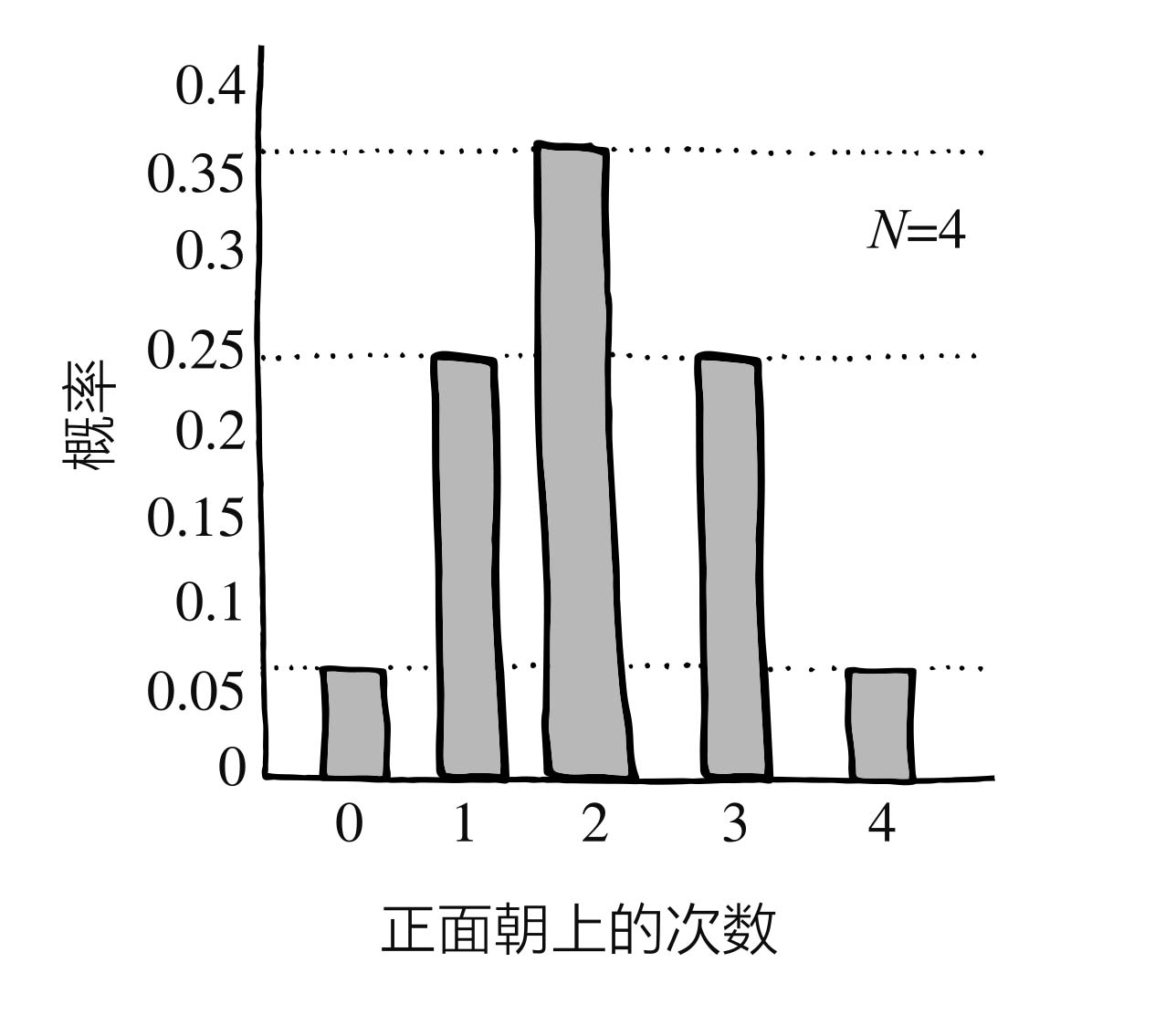
假定抛硬币的总次数为 N ，正面朝上的次数为 x ，那么对任何 N 、任何 x ，我们都能根据公式算出其具体概率，公式我就不写了（网上一搜就有），但我可以告诉大家，它会涉及 N 的阶乘、 x 的阶乘，以及 N - x 的阶乘等数值。
阶乘指的就是一个数乘以“它减1”再乘以“它减2”再乘以“它减3”……一直乘到数字1。比如5的阶乘就是5×4×3×2×1=120。数字只要稍微大一点，它的阶乘就会非常难算（阶乘的增速实在太快了，比如6的阶乘等于720，而10的阶乘等于3628800）。
事实上，我们关心的往往不是抛 N 次硬币正面刚好出现 x 次的概率。以赌博为例，现在有个人跟你说：“我跟你打赌，连抛100次硬币，正面朝上的次数会小于60。如果我输了，我就给你50英镑；如果我赢了，你就给我10英镑。”你觉得这个赔率合适吗？如果利用二项分布来计算，我们就得把100的阶乘、60的阶乘、40的阶乘代入公式；然后再把61的阶乘、39的阶乘代进去；之后再把62的阶乘、38的阶乘代进去……简直没完没了。伯努利还真是这么干的，这或许就是他的书花了20年才写完的原因。严格来说，他并没有写完，只是被迫放弃了。
当然，一旦有人真的算出了某个数的阶乘，比如253的阶乘——这个数一共有507位，结尾有62个0——他就可以把它记载下来，以供后人使用。即便如此，这一计算过程也相当枯燥、烦琐。
不过棣莫弗关注的并不是数字大小，而是曲线形状。
请再看看上面两个概率分布图：二者都是中间凸起，两侧逐渐平缓，只不过
N
=4的图像要更加平滑，显得更有规律。
抛硬币的次数 N 越大，曲线就会越清晰。比如 N =12时：
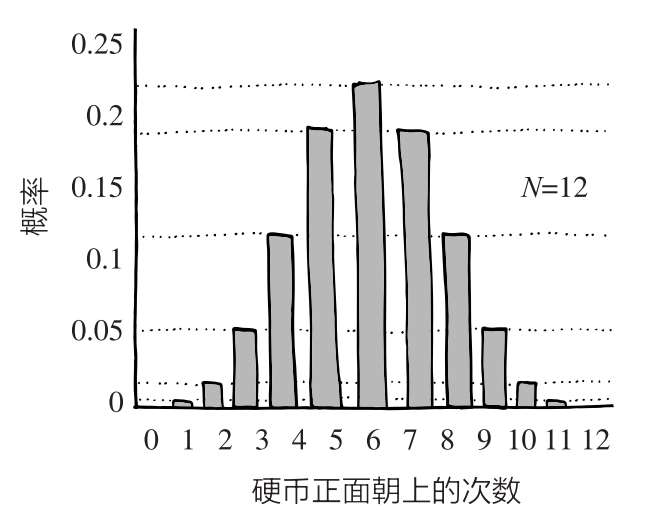
棣莫弗认为，与其费力地用公式去计算抛100次硬币出现60次正面的概率，还不如去分析一下曲线的数学表达式，然后利用该表达式来计算某种结果的概率。他说的这条曲线其实就是著名的正态分布曲线，也有人叫它钟形曲线（我认识的统计学家都不喜欢后面这个名字，因为大家觉得它根本不像个钟）。
我们现在来讨论一下亚伯拉罕·棣莫弗提出的两个概念，即“均值”和“标准差”——后面这个词直到150多年后才被人们创造出来。大家应当都知道什么叫均值（就是平均数），但我估计有很多人并不知道什么是标准差，可是很多专业人士在提到这个概念的时候并不会给出任何解释，搞得好像我们天生就该知道似的。其实标准差表示的就是数据在均值附近的离散程度。
假定你有3个孩子，你想知道他们的平均身高。为此你测量了每个孩子的身高，加在一起除以3，结果为160厘米。这就是均值。
有无数种组合可以让平均值为160厘米。比如三个孩子刚好都是160厘米；比如一个157厘米、一个160厘米、一个163厘米；再比如有两个孩子都是130厘米的8岁幼童，另一个孩子则是身高220厘米的大学篮球运动员。
这几组数据最重要的差别就是它们与平均值的差值不同。一般我们会用方差来衡量这种差别。得到方差之后，只要继续求出它的算术平方根，我们就得到了标准差。
方差的计算方式为：用每个孩子的身高减去平均值，然后计算出每个差值的平方（这样做是为了让每项数据都是正数），最后再求这些平方数的均值。
我们以157、160、163这组数据为例。用每个孩子的身高减去平均值会得到-3、0、3，计算每个差值的平方会得到9、0、9，最后计算这些平方数的均值
，6就是我们要求的方差。6的算术平方根约等于2.4，这就是标准差。
在8岁幼童和篮球运动员的例子中，用每个孩子的身高减去平均值会得到-30、-30、60，计算每个差值的平方会得到900、900、3600，最后计算这些平方数的均值
，这就是方差。1800的算术平方根约等于42.4，这就是标准差。
得到标准差之后，我们就可以用它来衡量每个值和均值的距离有多远（标准差通常简写为SD，或希腊字母σ）。
继续以8岁幼童和篮球运动员为例，这组数据的标准差为42.4，意味着两个8岁幼童的身高比均值低了30/42.4=0.7个标准差，而篮球运动员的身高比均值高了60/42.4=1.4个标准差。
有趣的是，如果数据呈正态分布，且样本量足够大，那我们就可以可靠地预测出与均值距离小于 x 个标准差的各个结果占全部结果的百分比。通常情况下，有68%的结果会落在与均值相差1个标准差的范围之内——这意味着如果你的身高比均值高出1个标准差，那么你的身高大约超过了84% [1] 的人口。此外，有95%的结果会落在与均值相差2个标准差的范围之内；有99.7%的结果会落在与均值相差3个标准差的范围之内。
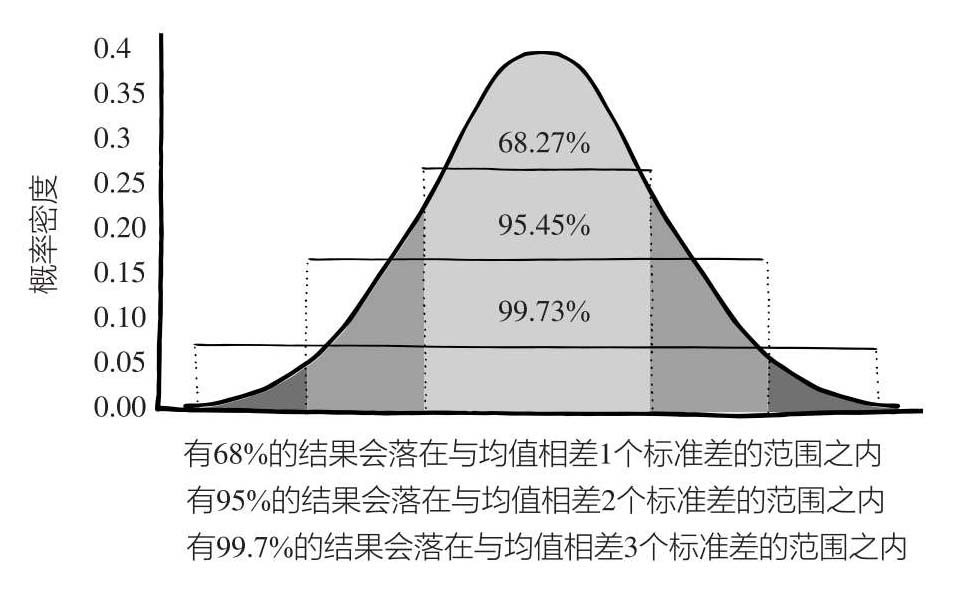
亚伯拉罕·棣莫弗证明，只要求出正态分布曲线的表达式（尽管当时的叫法并不是正态分布），我们就可以快速得出任何一种结果的概率的近似值。一番计算之后，他给出了自己的答案：有68.2688%的结果会落在与均值相差1个标准差的范围之内，而正确答案为68.2689%；有95.428%的结果会落在与均值相差2个标准差的范围之内，而正确答案为95.45%；有99.874%的结果会落在与均值相差3个标准差的范围之内，而正确答案为99.73%
（当时也没有“标准差”这个叫法，但他的确使用了标准差的概念，并将其视为衡量数据与均值的偏离程度的绝佳方法）。
由此一来，如果你想知道与均值相差特定距离之内的那些结果出现的概率有多大，那么你只需计算手中数据的标准差，然后将其代入棣莫弗计算出的曲线表达式即可。你再也不用花费大量时间去计算3600的阶乘了。
棣莫弗还发现，数据的精确度——标准差的大小——取决于样本数量，这其实就是伯努利一直在试图弄清楚的置信度问题的拓展形式。伯努利花费了20年的时间，日复一日地计算样本规模与置信度的关系，最终也没算出来到底需要多大的样本量，才能保证每1000次实验中有999次的结果与真值的差距小于2%。棣莫弗则研究出了通用算法，尽管精度有出入，但意义非凡。换句话说，伯努利只发现了样本量越大，结果越精确；而棣莫弗更进一步，实现了理论的量化。他的结论就是估计值的准确性和样本量的平方根成正比。
但是棣莫弗所研究的问题和伯努利所研究的问题没有什么不同：他们都在思考，在某种给定的前提之下，看到某种结果的概率是多少？比如前面那个“连抛100次硬币，正面朝上的次数大于等于60的概率”（答案是2.8%，即你赢钱的概率。50 ∶ 10的赔率太不公平了，你可千万别赌）。
棣莫弗和伯努利都没能回答后来被称为“反概率”的问题，而这才是概率学的核心内容。我们希望（或者说整个科学体系希望）统计理论能够告诉我们，如何根据已经掌握的结果去构建某个理论。
[1]
。——译者注