




大多数人会将17世纪中叶法国赌场中的故事作为概率论史的开端,但实际上早在16世纪的时候,意大利博学家吉罗拉莫·卡尔达诺就开始研究色子赌博中的概率问题了。比如他想知道,连掷4次色子,出现数字6的可能性有多大?将一对色子连掷24次,出现双6的可能性有多大?
他是这样计算的:首先,掷一次色子出现数字6的概率为1/6,约等于17%。一般我们在研究概率的时候并不直接写出百分比,而是将它表示为一个介于0和1的数值,并称之为 P 。所以这里我们将掷一次色子出现数字6的概率写作 p =0.17(实际上是0.166666…,但我四舍五入了)。
之后他做出了一个自认为合理的推测:连掷4次色子,出现数字6的概率就会变成前者的4倍,即4/6,约等于0.67。其实只要稍加思索,你就会意识到这肯定不对,因为如此一来连掷6次色子出现数字6的概率就变成6/6,换句话说这变成一个必然事件。但显然连掷6次色子是有可能每次都不出现数字6的。
令他感到困惑的是,虽然出现数字6的次数与总次数的比的确是0.67,但有时一次实验中你能看到3次6,有时一次实验中你1次6也看不到。这是因为他没有搞清楚“只出现1次数字6”和“至少出现1次数字6”是两回事。
事实上“连掷4次色子,至少出现1次数字6”的概率并不是0.67,而是0.52。尽管如此,在赔率为1 ∶ 1的情况下,你一直把钱押在“连掷4次色子会出现数字6”上面,仍旧是个正确决策。可是如果你在第二个问题上继续相信吉罗拉莫·卡尔达诺的结论,那你可就要亏大了。他的计算结果表明,既然一对色子一共有36种结果,双6在其中只出现一次( p =1/36≈0.03),那么将1对色子连掷24次,出现双6的概率就是前者的24倍,即24/36=2/3(就像第一个问题一样,他又得出了 p ≈0.67的结论)。
如果赔率仍旧为1 ∶ 1,那你就不该相信他的结论,而是应该把钱押在“连掷24次双色子不会出现双6”上面,因为“连掷24次双色子至少出现1次双6”的概率约为0.49,一直押这个选项会让你赔个精光。
一个多世纪后的1654年,安托万·贡博也对这个问题产生了兴趣。贡博喜欢将自己称为“梅雷骑士”,他除了热爱哲学,还痴迷赌博。和我们一样,他也意识到了卡尔达诺的结论有问题:一直把钱押在“连掷4次色子至少出现1次数字6”上面能让你赚钱,但一直把钱押在“连掷24次双色子至少出现1次双6”上面会让你赔钱。
多次试验之后,贡博得出了一个比卡尔达诺更靠谱的结论。可是他也困惑起来了:两个事件的概率为什么会不一样呢?4 ∶ 6和24 ∶ 36难道不是一回事吗?于是他邀请自己的朋友、数学家皮埃尔·德·卡尔卡维一起研究这个问题,但两人仍旧毫无头绪。无奈之下,两人又请来共同的朋友——天才数学家布莱兹·帕斯卡。

这个问题的答案其实并不复杂——卡尔达诺完全搞反了:重要的并不是它发生的概率,而是它没有发生的概率。
在连掷4次色子这个问题中,每次不出现数字6的概率都是5/6,即 p ≈0.83。如果连掷2次,那么2次都没有看到数字6的概率是0.83乘以0.83,约等于0.7。每多掷1次色子,你看不到数字6的概率都会下降17%。
如果连掷4次色子,那么数字6完全不出现的概率就是0.83×0.83×0.83×0.83≈0.48(可以简写为0.83 4 )。反过来,至少看到1次数字6的概率就是1-0.48=0.52,即52%。如果你在赔率为1 ∶ 1的情况下下注100次,那么你预计可以赢52次,小赚一笔。
假如我们现在每次掷2颗色子来赌双6,那么正如前面的分析,每次掷出双6的概率是1/36,即 p ≈0.03;没有掷出双6的概率就是1-1/36=35/36,约等于0.97。
连掷24次,1次双6都看不到的概率就是0.97 24 ,约等于0.51。因此,至少出现一次双6的概率就是1-0.51=0.49。如果赔率为1 ∶ 1,那么你下注100次预计只能赢49次,最终会赔钱。
(我们应当为安托万·贡博点个赞,他肯定花了很多钱才弄明白第一个赌局赢钱的概率是52%,第二个赌局赢钱的概率是49%。他甚至还正确地推测出,在第二个赌局中,投掷次数至少要提高到25,出现双6的概率才会大于50%。看得出来,他是真喜欢玩色子啊。)
赌场老手安托万·贡博感到有些意犹未尽,于是又问了帕斯卡一个问题:假定两个人正在玩一个赌钱游戏,比如扑克或色子,玩到一半就被迫终止,此时其中一人拥有明显的优势。这种情况下,怎样分配赌资才是最公平的?平分显然不合理,因为有人领先;把钱全给领先的那个人也不太合理,毕竟他还没有真的赢下赌局。
帕斯卡觉得这个问题很有意思,于是赶忙和皮埃尔·德·费马(以“费马大定理”而闻名天下)互通书信进行讨论。

这个问题可以追溯至几百年前的1494年。当时意大利数学家、方济各会修士卢卡·帕乔利也在研究类似的问题,并将结论写进了《算术、几何、比及比例概要》。

他构想了这样一个场景:两个人正在进行踢球比赛,每进一个球得10分,最先得到60分的人获胜。
 在比赛被迫中断的时候,其中一人已经得了50分,另一人得了20分。此时比赛的奖金该如何分配?
在比赛被迫中断的时候,其中一人已经得了50分,另一人得了20分。此时比赛的奖金该如何分配?
帕乔利认为,既然两人目前的得分一共是70,那么得50分的人就应当得到奖金的5/7。
45年后,前面提到的卡尔达诺竟公然嘲笑帕乔利,认为他的答案“荒谬至极”——考虑到卡尔达诺也没弄明白色子问题,我觉得他还是谦逊一点比较好。卡尔达诺设想了一个稍有不同的场景:两个人玩游戏,先得10分的人获胜,当游戏被迫终止时,一个人得7分,另一人得9分。按照帕乔利的观点,此时得7分的玩家应该分到7/16的奖金,都快占总奖金的一半了。得9分的玩家的奖金只比前者多一点,这显然很不公平,毕竟他只差1分就获胜了,而前者还差3分呢。
卡尔达诺的确给出了一个更好的方案。“他把关注点放在了‘双方还差多少分赢得比赛’上面,而不是‘双方已经得了多少分’上面。”普拉卡什·戈罗彻恩如此评价道。

可惜卡尔达诺离正确答案还是差了一点。他自己创造了一个叫作“胜利距离”的概念,来表示某选手距离胜利还有多远。选手差 X 分赢得比赛,他的胜利距离就是 X +( X -1)+( X -2)+…+1。假如该选手还差5分赢得比赛,那么他的胜利距离就是5+4+3+2+1=15。
在卡尔达诺的例子中,第一位选手得了7分,还差3分赢得比赛,所以他的胜利距离是3+2+1=6。第二位选手得了9分,还差1分赢得比赛,所以他的胜利距离就是1。如此一来,第二位选手应该分到6/(1+6)的奖金,看上去这的确公平了一些。
尽管这套方案的确比帕乔利的方案要好(至少更接近正确答案),但它仍是错的。
现在终于轮到帕斯卡和费马出场了。他们两人很快就看出了问题的关键:重要的不是选手距离终点有多近,也不是选手距离起点有多远,而是在剩下的所有可能性中,双方赢下比赛的可能性各占多少。
在写给费马的信中,帕斯卡设想了一个比较简单的场景:两个赌徒在玩一个游戏,先拿到3分的人获胜。双方各自下注32皮斯托尔(当时的一种金币),所以总赌资为64皮斯托尔。
假定在两个人都拿到2分的时候,游戏突然被迫终止。帕斯卡认为这种情况下钱很好分,每人拿32皮斯托尔就好了。
但如果此时两个人的得分不是2 ∶ 2,而是2 ∶ 1呢?帕斯卡认为,既然刚才在2 ∶ 2的情况下,奖金是两个人对半分,那此时就应该先给得2分的那个人分一半奖金,毕竟就算下一轮他输了,比分也只是2 ∶ 2而已。剩下那一半奖金怎么办呢?得2分的那个人可能会说:“这一半奖金有可能被你赢走,也有可能被我赢走,机会相等,既然如此,不如继续平分了吧。”如此一来,得2分的选手一共分到了32+16=48,即总赌资的3/4。
还有一种思路是,假定游戏继续进行,那么可能的结果共有4种:得2分的那个人既赢了第一轮,又赢了第二轮;他赢了第一轮,输了第二轮;他输了第一轮,赢了第二轮;他既输了第一轮,又输了第二轮。
只有在最后一种情况下,他才会输掉比赛。如果他赢了第一轮,那么第二轮的结果就不用看了,因为他已经得了3分,所以第一轮他有一半的机会直接赢下比赛。即便他第一轮输了,那第二轮中他仍有一半的机会赢下比赛。

由此可见,就像帕斯卡所分析的那样,如果两人不得不在2 ∶ 1的情况下终止赌局,那么总赌资最公平的分配方式的确是3 ∶ 1。
帕斯卡继续分析了其他情况。假定赌局被迫终止时,甲得了2分,乙只得了0分。如果甲在下一轮赢了,那比赛就结束了。如果甲在下一轮输了,那就又回到刚才2 ∶ 1的情况,我们已经知道这种情况下甲最终赢得赌局的概率为75%。按照帕斯卡的逻辑,甲会这样说:“如果下一轮我赢了,那我就会赢得全部赌资,即64皮斯托尔;如果下一轮我输了,那我也应当分走48皮斯托尔。因此,这48皮斯托尔肯定是属于我的。剩下的16皮斯托尔我们应当平分,因为咱俩拿到这笔钱的概率一样大。”
换句话说,甲最终赢得赌局的概率为7/8,即87.5%,所以最公平的分配方式就是甲拿走56皮斯托尔。用图来表示就是:
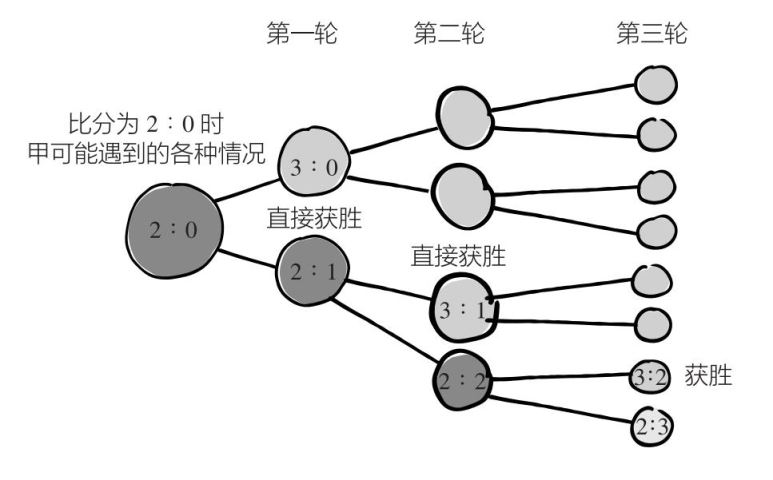
假如赌局被迫终止时,甲和乙的比分为1 ∶ 0呢?帕斯卡认为,这种情况我们可以再多分析一轮。如果乙赢了第一轮,那比分就变成1 ∶ 1,两个人重新站在了同一条起跑线;如果甲赢了第一轮,那比分就变成2 ∶ 0,我们已经知道此时甲最终赢得赌局的概率为7/8。在所有可能出现的16种结果里,有11种是甲最终赢得赌局,所以这种情况下甲应该分走总赌资的11/16,即44皮斯托尔。
现在大家应当已经意识到了,概率论关心的是给定情况下可能会发生什么,而不是已经发生了什么。不过前面的计算方法既费时又费力,所以帕斯卡和费马研究出了更便捷的方式。
我们的确可以耐心地做个汇总,但如果剩余回合数有很多,那计算量可就太大了。我们得把每一个可能出现的回合都分析一遍——需要分析的回合数等于甲最终赢下赌局所需的回合数,加上乙最终赢下赌局所需的回合数,再减去1。比如有一个三局两胜的双人比赛,甲以1 ∶ 0领先,那我们需要分析的回合数就是2+3-1=4(因为比分最高为3 ∶ 2,所以最大回合数是5,剩下的回合数最多是4),而4回合意味着2 4 (等于16)种可能性。之后你需要分析出其中有哪些可能性可以让甲最终赢下赌局,这一过程涉及大量的数字和标注,实在让人吃不消。
好在帕斯卡想到了一个轻松的方法。其实帕斯卡并不是第一个使用“帕斯卡三角形”的人——它在2世纪的印度、古代中国都很有名,它还有一个中文名字“杨辉三角形”——但他却是第一个将其用在概率问题中的人。这个三角形具体长这样:

它的“第0行”是1,其他各个位置上的数字都等于该数字左上角与右上角的和(如果左上角或右上角没有数字则视为0)。
帕斯卡发现这个三角形刚好对应着剩余回合数的各种可能性。仍然以甲乙比分为1 ∶ 0为例,剩余回合数最大为4,所以我们取第4行的数字来分析(最上面那个单独的1视作第0行)。第4行一共有1、4、6、4、1五个数,由于甲需要再赢两局才能获胜,所以我们去掉最左边的两个数,即1和4。把剩下的三个数6、4、1相加,再除以该行5个数的总和16,就是甲在1 ∶ 0的情况下最终赢下赌局的概率11/16,即 p =0.6875。
再试试其他例子。在甲乙比分为2 ∶ 1的情况下,比赛最多还能进行两回合,甲只要赢下其中任一回合就可以获得最终的胜利,因此我们可以用第2行的数字1、2、1来分析。首先我们去掉1,然后用剩下两个数字的和除以该行的总和,就得到了甲获得最终胜利的概率为3/4,即 p =0.75。这种方法相当便捷,能节省大量时间。
只要是双方每回合获胜概率相等的比赛,我们都可以采用该方法来分析,比如抛硬币、势均力敌的球赛。最大回合数为 X ,我们就用第 X 行的数字来分析(再次强调,最上面是第0行),该行所有数字的总和,就是所有可能出现的结果的总数。假如一共抛7次硬币,那么你就应该用第7行的数字来分析,即1、7、21那一行。该行所有数字的总和等于128,所以抛7次硬币一共有128种可能性。
现在假定你想知道抛7次硬币,某结果出现Y次的概率有多大,比如硬币正面朝上出现 Y 次。
有可能抛了7次全是背面朝上,1次正面都没看到。而在全部的128种结果当中,只有1种结果符合这一情形。
出现1次正面、6次反面的结果有7个。这是因为7次结果当中,只要正面恰好出现一次就行,具体哪次出现的并不重要。出现2次正面、5次反面的结果有21个(我就不一一列举了,你可以自己验证一下)。出现3次正面、4次反面的结果有35个。
看出规律了吗?1、7、21、35——这就是杨辉三角形的第7行。
因此,如果你想知道抛 X 次硬币,正面出现 Y 次的概率,你就可以在三角形中找到第 X 行的数字,然后自左向右找到第 Y 个数字(需要强调的是,最左侧的1视作第0个数字),用该数字除以该行所有数字的总和。比如你想知道抛7次硬币,正面出现5次的概率,那你就应该先找到第7行的数字,1、7、21、35、35、21、7、1,然后自左向右找到第5个数字,即21。所求概率为21/128≈0.164,接近1/6。
如果想求“正面至少出现5次”的概率,你只需把 Y 等于6和7的情况再加上去,即21+7+1=29,再用它除以该行总数128。帕斯卡在分析“赌资公平分配”问题时用的就是这一方法。
分析各种结果的概率有很多方法,杨辉三角形只是其中一种相对便捷的方式。如果每回合的可能性只有两种,就像抛硬币一样,我们就将其称为“二项分布”。
由此可见,当你想知道某件事发生的概率有多大时,你就需要分析一共有多少种结果符合该情形,以及所有可能的结果的总数。我想,你现在应该对“概率”有一个相对具象化的认知了。