托马斯·贝叶斯

伦敦东部肖尔迪奇区的老街地铁站附近有一个叫邦希田园的著名墓地。

不少名人都长眠于此，其中最著名的应该是威廉·布莱克、《鲁滨孙漂流记》和《瘟疫年纪事》的作者丹尼尔·笛福、《天路历程》的作者约翰·班扬。

不过对于像我这样经常步行往返于地铁站和英国皇家统计学会的人来说，邦希田园中最有名的逝者应该是托马斯·贝叶斯。

托马斯·贝叶斯是18世纪英国长老会的一名牧师，同时也是一位非专业的数学家。很少有人知道他生前写过一本神学书，以及一本分析牛顿微积分学的书，因为他最出名的作品是一篇名为《一个机会论问题的求解思路》（An Essay towards solving a Problem in the Doctrine of Chances）的论文。 贝叶斯去世之后，他的朋友理查德·普赖斯发现了这篇论文以及一些未完成的笔记。对其整理之后，普赖斯将其发表在了英国皇家学会的《自然科学会报》上。

而本书的核心内容，就是贝叶斯所提出的一个简单到难以置信的概念，即贝叶斯定理。毫不夸张地说，它或许是史上最重要的一个等式，可人们对贝叶斯本人却知之甚少，就连他的出生年份（1701年）都只是一个估计值。

加拿大滑铁卢大学的统计学名誉教授戴维·贝尔豪斯曾于2004年为《统计科学》杂志撰写了贝叶斯的个人传记。 他认为，关于贝叶斯的资料之所以这么少，主要问题在于他是一名“非国教者”——不信奉英格兰国教的新教徒。

想要理解这为什么会是个问题，我们就得回顾一下几个世纪之前发生的事情。小说《狼厅》的粉丝一定还记得，亨利八世为了娶安妮·博林为后，于1533年带领英格兰脱离了罗马教廷统领的天主教会。又娶了四任妻子之后，亨利八世于1547年离世。他死后，大主教托马斯·克兰麦于1549年推出了《公祷书》，并规定英国的所有教堂都必须在礼拜活动中遵循该书的指导。

亨利八世的长女玛丽一世并不认同《公祷书》的内容，于1553年废除了托马斯·克兰麦的主张。1556年，她以异教徒的罪名将托马斯·克兰麦绑在火刑柱上活活烧死，对那些“异端邪说”示以警告。几年之后，伊丽莎白一世又重新认可了《公祷书》的内容，自此，《公祷书》在信徒之中流行了一个多世纪，直至英国内战爆发。

英格兰共和国时期，从1649年查理一世被处死，到1660年君主制复辟这段时间，国家对礼拜形式的限制有所松动；然而到了1662年，议会又通过了新的《统一法案》，再一次确立了《公祷书》的地位，要求英格兰境内的所有礼拜活动都必须遵循《公祷书》的指导。

此时，很多神职人员已经习惯了共和国时期奥利弗·克伦威尔统治下的自由氛围，约2000人拒绝接受《统一法案》，其中大多数人是清教徒，结果就是他们被解除了职务，并被逐出了安立甘宗的教会。即便如此，其中仍有许多人选择继续布道（通常是在当地贵族的保护下），历史上一般将这些人称为“非国教者”或“不从国教者”。

1688年，英国通过了《宽容法案》，允许长老会信徒、贵格会信徒等非国教者享有礼拜自由，这意味着（与当时的天主教不同）他们再也不用偷偷摸摸地做礼拜了，但是他们的礼拜场所必须得到国家的许可。此外，这些人（其中就包括贝叶斯）还被禁止担任公职，禁止进入英国的大学。如此一来，非国教的学者和准牧师们就只能去苏格兰的大学（比如爱丁堡大学）或荷兰的大学（比如莱顿大学）学习、任教。

托马斯·贝叶斯来自一个相当富有的非国教家庭——其曾祖父理查德·贝叶斯因在谢菲尔德从事钢铁制造和餐具制作而发家致富。理查德和妻子爱丽丝（婚前姓查普曼）育有两个儿子，其中一个叫塞缪尔。和大多数名门望族一样（无论是否信奉安立甘宗），塞缪尔也成为一名牧师，并且非常幸运地在英格兰共和国时期达到大学入学年龄，进入剑桥大学三一学院学习，最终于1656年顺利毕业。尽管塞缪尔并没有信奉国教，但他还是成为北安普敦郡的一名牧师。不过后来《统一法案》颁发的时候，他又成为拒绝遵守该法案的2000名神职人员之一，并因此被调离了所在教区。理查德的另一个儿子约书亚是托马斯的祖父，他并没有从事神职工作，而是跟随理查德的脚步继承了家业。

这一时期的贝叶斯家族似乎十分热衷于非国教的传播。约书亚出资在谢菲尔德建造了一座非国教教堂，而他的女婿则成为另一座非国教教堂的创始人和牧师（虽然约书亚一共有4个女儿、3个儿子，但其中有2个女儿和1个儿子夭折了）。

约书亚的次子生于1671年，名字也叫约书亚 。小约书亚在英国北部的一所非国教学院学习哲学和神学，由于政府对非国教学者的骚扰和迫害，该学院曾多次被迫搬迁。毕业之后，小约书亚接连在伦敦多所非国教教会中担任牧师，先是在萨瑟克，后来又到了法灵登附近。根据戴维·贝尔豪斯的说法，小约书亚在信徒中非常受尊敬，大家认为他“既是一位传道者，又是一位博学者”。

另一方面，小约书亚也是一个典型的十分顾家的清教徒，拥有众多子女。1700年10月，他与安妮（婚前姓卡彭特）结为夫妻，但具体日期已无从考证，这或许是因为他们的婚礼是在非国教教堂举行的。没错，一个人的出生信息、死亡信息、婚姻信息全部由英格兰国教保存，非国教群体的各种登记信息则通常“保密或不公开，因为害怕遭受宗教歧视”。

出于同样的原因，小约书亚和安妮那7名出色的子女的出生信息也不得而知。这7个孩子全部顺利活到了成年阶段，这在当时是非常罕见的——18世纪早期出生的英国儿童约有三分之一会在5岁前夭折。 我们已知小约书亚的长子托马斯去世于1761年4月，享年59岁，所以据此可以推算出他有“80%的概率” 出生于1701年（也有可能是1702年年初）。托马斯的6个妹妹弟弟按出生顺序依次为玛丽、约翰、安妮、塞缪尔、丽贝卡、纳撒尼尔。同样，我们只知道这些人的去世年份和去世时的年龄（约翰去世时的年龄最小，1743年他去世的时候只有38岁；丽贝卡活到了82岁），但不知道他们确切的出生日期。

小约书亚这一家人的发展轨迹和当时其他富有的、受过教育的家庭差不多。约翰进入林肯律师学院攻读法律，并于1739年获得了律师资格。塞缪尔和纳撒尼尔像他们的祖父、曾祖父一样进入了商贸领域——塞缪尔卖家用纺织品，纳撒尼尔经营食品杂货。安妮嫁给了一位同阶层的富有的纺织品经销商，丽贝卡则嫁给了一位律师。故事的主角托马斯则选择跟随父亲的步伐，成为一名非国教牧师。

有一种说法是，负责教育少年托马斯的老师是贝叶斯家族的好朋友约翰·沃德，后来他成为剑桥市格雷沙姆学院修辞学教授、英国皇家学会会员。托马斯的父亲曾出资帮助约翰·沃德出版了著作《格雷沙姆学院教授们的生活》（ Lives of the Professors of Gresham College ）。约翰·沃德的传记作者表示，“在一番‘劝诱’之下，他承担了很多朋友的孩子的教育任务”，并在穆尔菲尔兹地区开办了一所学校。 还有一种说法是，负责教育少年托马斯的老师不是约翰·沃德，而是亚伯拉罕·棣莫弗，即概率论的伟大先驱之一，他曾被迫逃离法国，在伦敦靠当家庭教师谋生。不过，这种说法更多只是一种猜测。

托马斯是个相当聪明的年轻人。约翰·沃德于1720年（当时托马斯十八九岁）写给托马斯的一封信能够清楚地证明，托马斯·贝叶斯可以流利地阅读希腊文和拉丁文——毕竟信件就是用拉丁文写的——尽管约翰·沃德也在信中就托马斯的拉丁文写作能力给出了一些建议。

尽管贝叶斯家族富甲一方、人脉广泛，尽管托马斯聪慧过人，但他还是被英国的各所大学拒于门外，这一切只因他的家族没有信奉国教。1719年搬到爱丁堡之后，托马斯似乎拜入了逻辑学、形而上学教授科林·德拉蒙德的门下。1720年的那封信还包含一个信息，那就是托马斯对数学知识的掌握令约翰·沃德感到欣慰，他在信中写道：“你对各个科目的学习安排可谓井然有序，十分合理。同时学习数学和逻辑学，能够让你更清晰、更容易地理解二者对思维模式和认知模式的塑造起到了何种作用、做出了多大贡献。”

不过托马斯搬至爱丁堡的主要目的并不是学习数理知识，而是学习神学知识，以便为将来的牧师生涯打下坚实基础。1720年，托马斯进入了神学院。神学院里的资料表明，托马斯的主要研究方向是《马太福音》，最后一份研究记录的日期是1722年1月，据此我们可以推测在此之前他一直都在爱丁堡学习、生活。

由于我们对托马斯人生轨迹的了解是碎片化的，下一个时间节点不得不跳跃至1728年。我们知道托马斯在1728年之前的某天就已经出现在伦敦了，因为当年长老会、独立派、浸礼宗的共同委员会——托马斯的父亲小约书亚长期担任该委员会会员，有时还担任负责人——收到了一份牧师名单，上面写有托马斯的名字。此时的托马斯已经成为一名准牧师，但尚未进入教堂任职。之后在1732年——根据当年的一份名单——托马斯加入了父亲的事业，在法灵登附近的皮革巷的一个非国教教堂内任起了神职。1734年年初，他搬到了肯特郡的坦布里奇韦尔斯镇，开启了自己的牧师生涯。

目前我们只知道托马斯是个非国教者，但并不知道他的确切信仰。这或许意味着他信奉着一个相当小众甚至可能是难以被主流接纳的异端宗教。

可以确定的是，托马斯既不是安立甘宗教徒，也不是天主教教徒。虽然二者的教义不同，但区别并不大——在一般人眼中区别更小。天主教认为，只有通过教会才能获得救赎；而安立甘宗认为，只要教徒能够信仰耶稣并遵循他的旨意行事，那就算他一辈子没见过牧师，也能上天堂。天主教认为，圣餐仪式中的圣饼和圣酒真真切切就是基督的身体与血液；而大多数安立甘宗教徒认为圣餐仪式只是基督精神的一种寄托。不过两个教派都相信神圣的三位一体——圣父、圣子、圣灵——三个不同的位格都是上帝的同一本体、同一本质、同一属性。

某些非国教者有着非常不同的信仰，比如阿利乌斯派与苏西尼派完全不认可三位一体的说法（因此他们被主流基督教徒视为异教徒）。阿利乌斯派认为圣父才是至高无上的真神，他的儿子耶稣则是一个自始至终都存在着的、神性稍低一些的神，这意味耶稣在降临地球之前就已经存在了。类似地，苏西尼派也认为耶稣的神性要稍低一些，只不过他们认为耶稣并非一直存在，而是在诞生后才存在。后来这两个教派又衍生出了一个新的派别，即一位论派，该教派同样不认可三位一体，不过他们的理论更为激进——他们相信上帝是唯一真神，耶稣并不是神。

在18世纪，这些信仰在长老会中迅速普及开来。虽然贝尔豪斯认为“这些长老会成员的思想相当开放”，但实际上也没有开放到可以容忍各种思想存在的地步：1719年，埃克塞特市的长老会驱逐了两位传教士，即詹姆斯·皮尔斯和约瑟夫·哈利特，理由是两个人已经变成信奉阿利乌斯派的异教徒。

托马斯撰写的第一部作品是一本出版于1731年、名为《神的慈爱：试证神和政府都以生灵的幸福为宗旨，暨对〈神的正直：探究神在道德方面的完美性〉一文关于“美和秩序、惩罚行为的合理性、预先审判对于幸福的必要性”的论述的反驳》的神学著作。 虽然他并没有在书上署名（说实话，书名这么长，也没地方给他署名），但学界普遍认为这就是他的作品。他的好友理查德·普赖斯也在自己的文稿中表示，托马斯就是该书的作者。

具体来说，《神的慈爱》是一部讨论神正论的著作。托马斯试图在书中分析这样一个问题：假如上帝真的有大爱，是全知全能的，那他为什么会允许世界上存在罪恶？大卫·休谟曾引用伊壁鸠鲁的名言来描述该问题：“是不是上帝的确想阻止罪恶，但没有能力做到？如果真是这样，那他就不是全知全能的；是不是上帝的确有能力阻止罪恶，但他并不想这样做？如果真是这样，那他就不是真爱的。倘若他真的想阻止，也有能力阻止，那这世间又怎会有罪恶？”

托马斯这本书其实是对安立甘宗神学家约翰·鲍尔吉撰写的一篇神学文章的回应。约翰·鲍尔吉认为世上之所以存在苦难，是因为上帝的至善指的是“做正确和恰当的事情”，这种至善并不一定会符合人类的喜恶。 托马斯的观点与之相反，他相信上帝是慈爱的，上帝希望自己的子民幸福。不过现实情况是大部分世人都不幸福，所以托马斯花了大量篇幅解释为什么上帝有能力让我们幸福，也希望我们幸福，却没有这样做。这本书问世之后立即引发了大量争议，反过来这也导致它得到了广泛传播。

不过《神的慈爱》并没有提及托马斯自己的信仰。虽然托马斯的父亲小约书亚是一位“包容的、能够接纳各种不同观点的加尔文主义者” ，但根据贝尔豪斯的观点，托马斯很可能是一位阿利乌斯派信徒或苏西尼派信徒，并且“即将成为一名一位论派信徒”。贝尔豪斯表示：“他不是那种寻常的、传统的基督徒。尽管他曾接受长老会牧师的培训，但他很可能是一名苏西尼派信徒。”

证据来自托马斯的社交圈。托马斯和詹姆斯·福斯特是朋友兼同事——詹姆斯·福斯特也是一名非国教牧师。此外，詹姆斯·福斯特本人还和另外两名因信奉阿利乌斯派而被驱逐的埃克塞特牧师是好朋友。詹姆斯·福斯特写过一本名为《宗教的基础论》（ An Essay on Fundamentals in Religion ）的手册 ，他在手册中表示三位一体并不是基督教的基本信条。在我看来，这种思想简直是异教中的异教。

托马斯还有一位叫威廉·惠斯顿的同事，他是艾萨克·牛顿的学生，也是牛顿在剑桥大学的卢卡斯数学教席的继任者。某次早餐会上，这两位同事一起问托马斯，周末在本地安立甘宗教堂举办的讲道活动是否包含《亚他那修信经》的内容（该信经阐释了三位一体理论）。威廉·惠斯顿表示，如果包含这部分内容，他就当场辞去神职，托马斯立即安慰他说大概率不包含。

托马斯死后还给约翰·霍伊尔、理查德·普赖斯留下了200英镑。这两个人都是伦敦地区的非国教牧师，都信仰阿利乌斯派，他们所在的教会最后都改信了一位论派。前文提及，理查德·普赖斯是托马斯的挚友，托马斯去世之后，正是他帮忙整理、发表了那篇包含贝叶斯定理在内的著名论文。

托马斯·贝叶斯身边的同龄人大多出身于贵族家庭，接受过大学教育，甚至有不少人拿到了神学博士学位。 他的社交圈中有很多像约翰·沃德、威廉·惠斯顿一样德高望重的人物，仅凭这一点就能看出他生活的环境有多上流。来到坦布里奇韦尔斯之后，托马斯继续与名门望族、权贵显赫之辈打交道，其中最重要的一位应当是第二代斯坦诺普伯爵菲利普·斯坦诺普。当时坦布里奇韦尔斯的“主要产业是旅游业” ，所以交通相当便捷，人们从伦敦坐马车只需一天便可抵达这里。当地最出名的旅游资源是深受大众喜爱的、泉水全部自产的大型温泉。菲利普·斯坦诺普7岁的时候继承了亡父的爵位。由于他家的“志奋领庄园”距离坦布里奇韦尔斯只有几英里 的路程，从20多岁开始他就成为当地的常客。菲利普·斯坦诺普出生于1713年，比托马斯要年轻一些。

这位年轻的伯爵算得上一位狂热的数学爱好者。小时候，他的叔叔及监护人曾逼迫他放弃数学，把兴趣转向文学艺术，可是成年之后，他立即重新拾起对数学的热爱。他的同辈曾这样评价他：“他阅读了大量和神学、形而上学、数学相关的书。 他的笔记本上总是写满了各种数学符号，以至于有一半人以为他是变戏法的，还有一半人干脆把他当成傻子。”

菲利普·斯坦诺普为科学家和数学家编织了一张社交网络，托马斯、格拉斯哥大学的数学家罗伯特·史密斯（菲利普·斯坦诺普曾帮忙出版他的遗作）、化学家约瑟夫·普里斯特利（氧气的发现者）、神学家兼科学家约翰·埃姆斯（牛顿的好朋友）都在这个圈子中。这张关系网中的所有人都是来自不同教派的非国教者，而且大多是出身名门望族的科学爱好者、数学爱好者。

贝尔豪斯认为，以现代人的标准来看，“与其说托马斯是个学者，不如说他是个业余爱好者兼艺术家。他做研究更多是为了自娱自乐，而不是为了在学术上有所成就”。

菲利普·斯坦诺普和托马斯都是聪颖之辈，而且他们的工作并不繁重，闲暇时光较多，可以把大量精力花在数学上。贝尔豪斯表示：“18世纪的富人特别热衷于参与各种科学活动，就像现代的富人总是喜欢投资各种球队。”

近些年，人们在菲利普·斯坦诺普的遗物中发现了大量他与托马斯往来的书信。根据信中内容我们可以推测，两人相识于18世纪30年代，契机则来自托马斯所写的一篇名为《微积分浅谈》（An Introduction to the Doctrine of Fluxions）的论文。

当时哲学家乔治·贝克莱正在不遗余力地抨击牛顿的微积分理论，托马斯为了支持牛顿而写下这篇论文。没错，托马斯是牛顿坚定的追随者。贝尔豪斯表示：“有些非国教者不敢传播数学知识，因为他们害怕被人看作牛顿科学的拥护者，进而被贴上‘无神论者’的标签。但大多数非国教者都认为学习数学至关重要——有了数学，你才能弄懂上帝所创造的这个宇宙的运转规律。”

乔治·贝克莱认为牛顿的理论犯下了“除数为零”的错误：一个关键的方程中，分母居然可以等于零，可见“微积分学说”在本质上是矛盾的。为了反驳这种言论，托马斯试图在自己的论文中为牛顿的理论给出更严格的定义，让方程的每一项都不再有歧义。

之后托马斯又对无穷级数及其与导数的关系做了一些研究。“导数”是图表中斜率的变化率。假如现在有一幅关于距离（单位为米）和时间（单位为秒）的图形，线条的形状反映了速度（单位为米每秒）的情况。如果线条是直线，那速度就是恒定的；如果线条是曲线，那速度就是变化的。导数可以精确求出曲线在某一点的斜率，这样我们就能算出任意给定距离或时间下的速度。更进一步地，我们知道速度的变化量除以时间就是加速度，加速度是距离和时间的二阶导数。

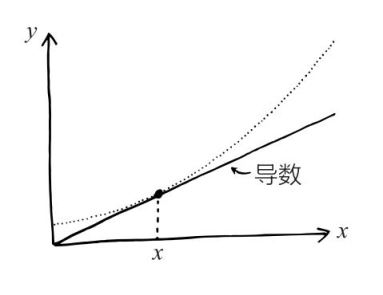
而无穷级数指的就是无穷无尽的级数。比如“ x =1+2+3+4+5…”就是一个无穷级数，等式右边可以按照规律一直加下去，所以 x 等于无穷大。不过，并非所有无穷级数都等于无穷大，比如“ x =(1/2)+(1/4)+(1/8)+(1/16)+(1/32)…”也是无穷级数，但它等于1。

托马斯证明， y 在某一点的导数等于 y 展开的无穷级数在 T 时刻的值，减去它在 T +1时刻的值的一半，再加上它在 T +2时刻的值的三分之一……以此类推。直到托马斯和菲利普·斯坦诺普双双离世之后，人们才在斯坦诺普的手稿中发现了这一精巧的公式（那张遗稿以寥寥数字记下了这一信息：“1747年8月12日，托马斯在坦布里奇韦尔斯向我介绍了这个定理”）。贝尔豪斯表示，直到25年之后，法国数学家拉格朗日才再一次独立提出了该定理。

托马斯就是在这个时候开始对概率论产生了浓厚的兴趣。不过在介绍贝叶斯定理之前，我们有必要回顾一下概率论的发展史，了解一下那些为概率论做出过重要贡献的人。 YUH8233SrNtgaPlUv1DxZWUTKjwLMq0I5g4RacYrCJRbH95bIqxsuFWcvTuSCq6x