下载掌阅APP，畅读海量书库
立即打开
在数学成就之外，贝叶斯对概率论还做出了很大的哲学贡献。到目前为止，我们一直都在把概率当作一个真实存在的事物。我们说抛1次硬币，正面朝上的概率是50%；抛100次硬币，正面至少有60次朝上的概率大约为2.8%。我们说出这些话的时候，从来没有怀疑过其真实性，好像它们本就是存在于世界中的某些事实。贝叶斯改变了这一切。
在贝叶斯看来，概率只是“世界不为人知的那一面的一种描述方式”
——引自英国皇家统计学会前会长、剑桥大学前“公众风险理解温顿
教授”戴维·斯皮格霍尔特爵士。
换句话说，贝叶斯认为概率是一种主观的东西，是人类对未知领域、对真理的最佳推测的一种表述。它不是这个世界的天然属性，而是我们对世界的一种理解。假如你在我面前抛了一枚硬币，然后用手掌遮住结果，问我“正面朝上的概率是多少”，那我可能会回答“50%”，前提是我相信你没有动手脚。不过，如果我知道你是个魔术师，或者是世界上最狂热的“错版硬币收藏者”，那我可能会给出不同的答案。
贝叶斯在论文《一个机会论问题的求解思路》中指出，想要实现“统计推断”——再次强调，“统计推断”研究的是“如何根据已经得到的结果推算某个假设成立的概率”；而“概率推断”关心的是“如何根据已经构建好的假设推算出现某个特定结果的概率”，二者思路完全相反——我们就必须弄清某理论在一开始就是正确理论的可能性。也就是说，我们必须把自己对该事件的主观信念考虑进去。
为了解释这一观点，贝叶斯用一个在桌上滚动的小球来比喻（注意，这并不是传统意义上的台球。史蒂芬·斯蒂格勒认为：“后来很多作者把这个比喻总结成台球，但贝叶斯的比喻并没有如此具体、如此不严谨。”
虽然戴维·斯皮格霍尔特爵士也将其称为“台球”，但他还加了一个补充说明：“身为长老会的牧师，贝叶斯只是将其称为‘桌上的小球’。”
）。该比喻具体来说是这样的：桌子处于视线之外，此时桌上正有一个白球在滚动，其最终位置完全随机。“桌面上每一处都是一模一样的，小球停留在每一处的概率也是一模一样的。”
白球停稳后，它就会被人移走。人们会画一条穿过球心的、垂直于桌子边框的直线，但你不会被告知这条直线在哪儿。之后又有一些红球滚到了这张桌子上，你会被告知有几颗红球在这条线的左边，有几颗红球在这条线的右边。你的任务就是估算这条直线的位置。
假定红球一共有5颗，落定之后有人告诉你，直线左边有2颗，右边有3颗。
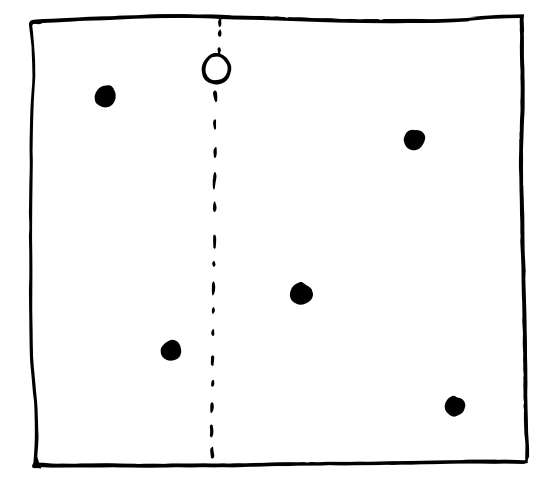
你觉得这条线会在哪里？贝叶斯认为，这条线最有可能的位置是桌子的3/7处（自左向右）。
凭直觉，你可能会觉得这条线应该在2/5处，毕竟左右两侧红球的数量是2 ∶ 3。但贝叶斯认为，我们在分析问题时必须考虑先验概率——在得到任何实验结果之前你对问题的最佳猜测。
可是最佳猜测从哪儿来呢？实验之前我们不是什么都不知道吗？那条线在哪儿都有可能。其实，“等概率出现在任何位置”也是一种先验预测：从你的主观视角来看，这条线可能存在于桌面两侧之间的任何一个位置，每个位置的概率都一样大。
你甚至可以画出相应的概率分布图——在得到红球信息之前，这条线出现在某一位置的可能性有多大：
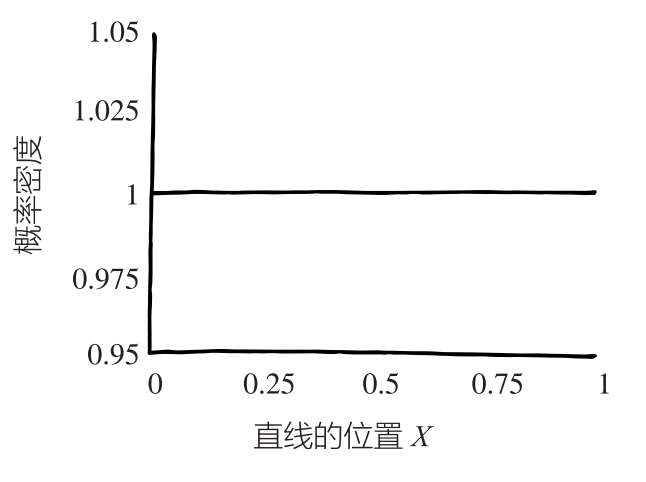
如果你完全不知道该如何判断这条线在哪里，那就意味着下一颗红球落在这条线左侧的概率是50%。因为这条线可能在最右边，此时红球必然在它的左侧；直线也可能在最左边，此时红球必然在它的右侧；直线也可能在正中间，此时红球在左右两侧的概率相等；红球还可能以相同的可能性出现在其他位置。所有可能出现的位置的平均值，恰好就在中间。
贝叶斯有一个相当关键的见解——你必须将所有新得到的信息添加到已知信息之上。尽管本例中的已知信息十分有限，但我们绝不能忽视它的存在。
这意味着，你不应该只根据5颗红球的位置就判断说：“这条线最有可能位于2/5处。”而是应该把先验信息也考虑进去。贝叶斯认为，计算概率的方式不是左侧红球数除以全部红球数，即2/5，而是左侧红球数加1，再除以全部红球数加2，即3/7。戴维·斯皮格霍尔特爵士表示：“这相当于你已经提前扔出了两颗‘假想红球’，它们分别落在直线两侧。”
虽然这看起来有点怪，但只要想一想5颗红球全落在同一边的情况，你就明白了。比如，假定5颗红球全落在直线左侧，那如果不考虑假想红球的情况，我们就会得出“下一颗红球有5/5=100%的概率落在左侧”的结论，这显然是荒谬的——你显然不会有这么大的把握。如果把贝叶斯的假想红球考虑进去，这一概率就从5/5变成6/7。而且，不管有多少颗红球落在同一侧，你都不再会有100%的把握去判断下一颗红球的位置了。比如现在有100万颗红球全落在了左侧，那么根据贝叶斯的理论，下一颗红球仍旧有可能出现在右侧，其概率为1/1000002。每一条新信息都能让你更接近“100%的把握”，但你永远不可能真的达到“100%的把握”。
此外，贝叶斯也谈到了概率分布的问题。现在我们已经知道了这条线最有可能出现的位置，但实际上它也有可能出现在预测值附近的某个位置，只不过概率较低一些；或者出现在更远的某个位置，概率要更低一些。它甚至也有可能出现在最右边的某个位置——3颗红球刚好全部挤在最右边，只不过这种可能性的概率极低。据此我们可以画出相应的概率分布图。
我们画过概率均匀分布的样子——呈一条水平直线。在得到5颗红球的新信息后，我们可以通过较为复杂的数学方法重新绘制概率分布图，它长这个样子：
这就是后验概率分布图——新信息出现，先验判断得到了更新，你对直线位置的预估产生了变化。
可是，如果继续有新信息出现，那么此时的后验判断
又会变成后者的先验判断。如果再扔5颗红球，那你可能会再经历一遍同样的计算过程，不过新的概率分布图很有可能会变得更窄，更集中在真值附近。
前面出现的所有案例，包括癌症筛查、新冠病毒检测、判断疑犯，使用的都是这套分析方法。我们先分析先验概率（癌症的发病率是多少），再把新得到的信息加上去（具有某一灵敏度、特异度的阳性测试），最后得出一个新的后验概率。
需要强调的是，这一切都是主观的。这些概率不是随机给出来的，每个人心中的先验概率也不一定是相等的——如果你的先验概率是每次掷色子约有1/6的概率掷出6，而我的先验概率是每次掷色子约有5/6的概率掷出6，那么你很有可能比我更接近真实答案，因为大部分色子都是公平色子。你可以根据自己的信念去调整先验概率，不管这个信念是对是错，它都是主观的（当然，假如色子的确是公平的，实验也进行了几百次，我对贝叶斯理论掌握得也很到位，那我就会不断地根据新信息调整自己的判断。当我们发现出现数字6的概率大约为1/6时，我的结论就已经和你的差不多了）。
贝叶斯的论文《一个机会论问题的求解思路》很可能写于辛普森1755年的论文之后，而且在很长时间内都无人知晓——贝叶斯离世之后它才被发表。法国数学家皮埃尔-西蒙·拉普拉斯于1774年独自得出相同结论时，应当并不知道这篇论文的存在。史蒂芬·斯蒂格勒认为，贝叶斯并不是很在意这篇论文是否发表——1760年，在离世前4个多月，他写了一份遗嘱，表明自己已经预感到将不久于人世。“其实如果他愿意，他本可以在遗嘱中将自己的研究成果交给英国皇家学会”
，毕竟他当时已经是会员了。可最终他并没有这样做，而是把这篇论文和其他手稿，以及100英镑一起，以遗产的形式交给了好友理查德·普赖斯（尽管贝叶斯当时根本不知道理查德·普赖斯到底在哪儿——“他可能正在纽因顿绿地传教”，贝叶斯在遗嘱中这样写道
），而理查德·普赖斯很清楚这些遗稿的重要性。