下载掌阅APP，畅读海量书库
立即打开
我有个表哥，名叫杰拉德·格兰特，小时候他爱给我们讲鬼故事。他说，他曾在月光下看见他祖父的鬼魂在一尊圣马利塑像前祷告。还有一次，他在爱尔兰一个荒凉的地方露营，醒来时发现帐篷外炉子上的锅里，培根和鸡蛋正发出嗞嗞的声响。“肯定是那些小家伙，”他说，“爱尔兰的小妖精。”甚至还有一个故事，一个人预见到了自己的死亡。“他看到自己走在自己身后，”杰拉德告诉我们，带着一种不祥的预感，“那是他的分身。一个跟他一模一样的幽灵。于是他知道，自己快要死了。”后来他真的死了，至少杰拉德是这么说的。
你或许觉得，分身的故事在一本关于物理和数学的严肃书里应该没有容身之地。但既然我们讲的是庞大数字的故事，你应该已经料到，总有些事出乎意料。这个故事从 古戈尔 （googol）开始：
10，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000，000
它相当于在1后面加100个零，或者说10 100 。古戈尔这个数有一种十进制的优雅，甚至有一丝堕落之美。就任何现实的标准而言，我们都可以放心地说它是一个大数字。如果你买彩票赢了1古戈尔英镑，你就可以给自己买一艘豪华游艇，甚至一支豪华游艇船队，外加一艘航空母舰，要是你愿意，或许你还能买下这颗星球上的所有船。你甚至可以买下美国。买下整个美国可能只需要不到50万亿美元，对像你这样的古戈尔富翁来说，这简直等于不要钱。你真的可以买下一切：可观测宇宙中的每一个分子、每一个原子、每一个基本粒子。宇宙中大约有10 80 个基本粒子，你完全买得起，甚至能给每个粒子出到百万英镑的三次方以上的价钱。
古戈尔的传奇实际上始于米尔顿·西罗蒂（Milton Sirotta），一个9岁的小男孩，他的爱德华叔叔恰好是哥伦比亚大学杰出的数学家爱德华·卡斯纳（Edward Kasner）。卡斯纳属于一个特殊的群体，他们有自己的独特时空，赫尔曼·闵可夫斯基、卡尔·史瓦西（Karl Schwarzschild）和罗伊·克尔（Roy Kerr）都是这个群体中的一员。卡斯纳的时空和你体验过的任何宇宙都不一样。如果你坐在他的宇宙里，你会发现空间的某些方向正在膨胀，而另一些方向正在压缩，就像一块一头被拉伸，另一头被挤压的面团。但这个可怕的世界跟古戈尔无关。想出这个概念的时候，卡斯纳正试图探索无限的广袤。他想强调的是，比起无限，任何有实际意义的、看起来非常大的数都显得那么渺小。为了揭露这个真相，他决定使用一个1后面有100个零的数字，但他需要给这头小巨兽起个名字。10 100 ，或者100的多少次方，感觉都不合适。他的侄子米尔顿提了个好建议：古戈尔。
有趣的是，我们惊叹于这个数字如此大，但卡斯纳最初引入它是为了表明它有多小。他和侄子很快又想到了另一个神奇数字： 古戈尔普勒克斯 （googloplex）。按照米尔顿最初的定义，古戈尔普勒克斯相当于1后面跟着“直到你写累了”那么多个零。为了弄清这个数到底有多大，我做了个实验：我1分钟能轻松地在1后面写135个零，而且一点儿也不累，所以古戈尔普勒克斯肯定比古戈尔要大。要加大一点难度，我们完全可以请一位像兰迪·加德纳（Randy Gardner）那样耐力超强的人来写。20世纪60年代中期，10多岁的兰迪·加德纳在一项旨在研究睡眠剥夺有何影响的实验中创造了11天零25分钟不睡觉的纪录。如果他在这段时间里一直在写古戈尔普勒克斯——以我那样的轻松速度持续不断地书写，那他应该能在1后面写出2 141 775个零。这个数很大，但卡斯纳决定给古戈尔普勒克斯下一个更清晰的定义，他最终确定下来的数远超米尔顿的标准。卡斯纳将这个新数字定义为1后面有古戈尔个零。想想看吧：古戈尔个零！10的古戈尔次方！虽然这个数看起来大得不可思议，但卡斯纳想强调的是，有无数个数比它大。
比如古戈尔普勒西恩（googolplexian）。它相当于1后面有古戈尔普勒克斯个零。古戈尔普勒西恩又被称为“古戈尔普勒克斯普勒克斯”（googolplexplex）或者“古戈尔双重普勒克斯”（googolduplex）。事实上，后面这两个定义更强大，因为它们允许我们利用递归的理念搭建一座庞大的数字高塔。你可以从古戈尔双重普勒克斯跳到古戈尔三重普勒克斯（googoltriplex），也就是1后面有古戈尔双重普勒克斯个零。然后是古戈尔四重普勒克斯（googolquadruplex），即1后面有古戈尔三重普勒克斯个零，以此类推。 [1]
我们扯远了。我们在古戈尔和古戈尔普勒克斯这里暂停一下，因为它们足以阐释物理学下一块了不起的拼图，带领我们重温分身的警世故事。你看，当我们开始想象古戈尔级宇宙，甚至古戈尔普勒克斯级宇宙，你就可以问一问，
分身是否真的存在
。所谓“古戈尔级宇宙”，我指的是，无论你采用现实中的什么距离单位（米、英寸或者弗隆
，区别都不大），这个宇宙的直径至少达到了古戈尔的量级。古戈尔普勒克斯级宇宙甚至更大，同样在现实中的距离单位下，它的直径达到了古戈尔普勒克斯的量级。
宇宙分身的概念始于麻省理工学院物理学家马克斯·泰格马克（Max Tegmark）。
[2]
他想象了一个广袤的宇宙，在任何望远镜都观察不到的地方，有许多远方的世界，在这个宇宙中某个遥远的地方，有一个和你一模一样的分身，他和你的发型完全相同，鼻子完全相同，就连想法都完全相同，他估算了你和这个分身之间的距离。当我第一次听到他的这个说法时，我满腹狐疑。无意冒犯，但这个宇宙为什么需要另一个版本的你，或者我，抑或是詹姆斯·柯登（James Corden）
？然后我坐下来，琢磨了一会儿。泰格马克的宣言源于全息世界，所有物理学中最宏大的假象。
我决定借助一些重要的理念，自己估算一下这段距离，正是这些理念引领全世界最伟大的几位物理学家得出了全息真相的设想。这个故事我需要用两章来讲，从古戈尔到古戈尔普勒克斯。故事从熵开始，从它对人类和人类大小的黑洞来说可能意味着什么开始。它带领我们深入量子理论那个神奇的微观世界，理解你之所以为你、你的分身之所以为你，这到底意味着什么。最后，我估算的结果比泰格马克的保守一点，但还算相去不远。根据我的估算，以米、英里（或者你愿意用的任何现实的单位）来衡量，你和你的分身之间的距离介于我们下面要介绍的两个庞然巨数之间：古戈尔和古戈尔普勒克斯。换句话说，你在古戈尔级宇宙里找不到自己的分身，但在一个古戈尔普勒克斯级宇宙里，他几乎必然存在。他甚至可能正在读一本和你手中一模一样的书，就像此时的你一样。
照照镜子，你看到了什么？每当我看镜子里的自己时，我往往会注意到斑斑点点的灰发，或者从我西班牙裔祖母那里继承到的纵横交错的皱纹。这些东西不会困扰我。说到底，我是个理论物理学家。作为专业人士，我们并不以外貌焦虑著称。但我真正看到的是时间的流逝——熵的增加。
要估算你和分身之间的距离，我们首先必须理解熵，以及熵的增加有多恐怖。熵常常被误传，人们毫不严谨地把它当成无序或者破坏的代名词。事实上，我们应该把它当成一个捕手，或者一位狱卒，这样更好理解。这位狱卒会不可逆转地锁住能量，其中包括有朝一日整个宇宙的所有能量。暂且想象一下，你身处维多利亚时代的英国。你看到滚滚黑烟从北方一座城镇的烟囱里升起。工人们像蚂蚁一样涌入工厂，他们鳞次栉比的家园被笼罩在弥漫的邪恶烟雾之中。在那个年代，人类第一次暴露出贪得无厌的胃口：更多机器、更多能量、更多动力。但这不可能永远持续下去，不是因为气候变化会扼杀这颗星球，而是因为熵和令人战栗的熵增。
熵的故事从维多利亚时代的这些工厂开始，它诞生在一位名叫萨迪·卡诺（Sadi Carnot）的年轻法国军事工程师充满好奇的脑袋里。受到工业革命浓烟和轰鸣的启发，卡诺创建了自己的物理学分支——热力学（thermodynamics）、专门研究热的动力学，以及热和机械动力的关系。你每一次点燃燃料，都是为了把它产生的热转化为某种有用的东西，比如汽油在汽车发动机里快速燃烧，释放出灼热的气体，推动活塞。然后活塞的运动通过曲轴传递给车轮，推动汽车向前行进。19世纪初，汽车还没有诞生，不过卡诺理念的适用范围远远超出了他那个年代的火车和工厂。按照他的理解，发动机的关键在于温度差。只要存在温差，你就能汲取有用的机械功，比如火车向前运动，或者为一台机器提供动力。但热总是会从温度高的地方传向低的地方，直到抹平温差，然后到此为止。你无法再汲取任何功，也无法推动任何机器。
你也许觉得你可以设法转移热，甚至利用你的机器让温度再次升上去，或者降下来。你希望重新创造温差，好再汲取一些有用功。这从某种程度上说可以实现，但卡诺证明了以这种方式转移热，需要你投入的有用能量总是比产出的更多。以汽车为例，如果能让汽车的动能重新转化为燃料，你就不用费劲跑去加油站了。如果你足够聪明，你也许能 回收一部分能量 ，但不会有你最初投入的那样多，最终你的发动机会失去动力。问题在于，在现实世界里，你总是会失去一点儿东西。你永远不可能彻底重置你的发动机，至少不会是免费的。对维多利亚时代那些想知道自己的工厂能产生多少利润的创业者来说，这方面的知识十分重要。正如我们即将看到的那样，理解“熵”这个疯子如何扼杀全宇宙的所有生命，这对我们来说也很重要。
很难说卡诺的工作中最了不起的地方是什么：是他在所有人对能量守恒（这个我们后面会聊）都还一无所知的时候就弄清了这一切，还是虽然他构思的热模型错得离谱，却歪打正着地得出了正确的结论。和他同时代的很多人一样，卡诺认为，热的行为方式就像液体，它是一种名叫“热质”（caloric）的自我排斥物质。热质并不存在。但这不重要，多亏了卡诺去芜存菁、厘清重点的独特能力。这些想法发表后还不到4年，卡诺从军队里退役，又过了不到5年，他去世了。当时他才30岁左右，致使他丧生的那场霍乱疫情在1832年夺去了近2万巴黎人的生命。为了防止病毒传播，卡诺的遗体和他的大部分遗物都被火化了，包括大量未发表的研究论文。直到几十年后，他的才智才得到外界的认可，而那些被烧掉的手稿上的内容，我们永远无从知晓。这是个悲剧故事，而且正如我们即将看到的那样，在热力学历史上，类似的悲剧还将重演无数次。
尤利乌斯·冯·梅耶（Julius von Mayer）的故事就是其中之一。冯·梅耶是一位医生，1840年，他在一支驶往荷属东印度群岛的船队中做随行医生。当时有一名水手生病了，冯·梅耶需要给他放血。他切开病人的血管，试图借此减轻其症状。这在当时是一种常见的治疗手法，但冯·梅耶由此发现了一件惊人的事情。他注意到，这些水手的静脉中流淌的血液和动脉里的一样是鲜红色的。在气候更寒冷的地区，比如他的祖国德国，朝肺部回流的静脉血的颜色要比这暗得多。这是因为静脉血缺氧，原有的氧已经被消耗，通过食物的缓慢燃烧来为身体取暖。冯·梅耶意识到，在热带的阳光下，水手只需要燃烧更少的热量就能保持温暖，所以他们的静脉中流淌的血液氧含量比人们预期的要高。这意味着身体通过食物产生的热和来自太阳的热是等价的。冯·梅耶由此推测，所有的热都等价于 能量 。
只是放了一点点血，这位随船医生就建立了热力学第一定律：能量永远不会被创造出来，也不会被摧毁。它是一头永恒的变形兽，一直都在，从一种形式转化为另一种形式。他还确认了热只是能量的另一种形式，这和当初启发卡诺的古老的热质模型完全不一样。冯·梅耶将自己的发现整理成文，但他的工作没有得到任何认可。由于缺乏物理学方面的训练，他的论文写得很差，而且有很多错误。英国物理学家詹姆斯·焦耳（James Joule）独立得出了相同的结论，他在科学上更为严谨，这意味着这个发现几乎完全被归功于他。冯·梅耶很快还将遭到另一个打击，他的两个孩子在极短的时间内相继丧命。他陷入了抑郁，试图自杀，最后在精神病院度过余生，私人生活的悲剧和专业领域的挫折摧毁了一个才华横溢的人。
没人能逃脱热力学的诅咒。它终将捕获我们每一个人，无一例外，包括我们生活的这个宇宙的每一个角落。要理解这必将降临的厄运，我建议你给自己先沏一杯热茶。茶刚沏好的时候，你会注意到，这杯茶和周围的空气之间存在温差。根据卡诺的理论，你应该能在茶和空气之间安装一个小小的热引擎，将这些热转化为有用的机械功。说不定你甚至可以驱动一台很小的马达。当然，如果你分了心，没来得及安排这些事，茶放得太久，热量就会从茶里散发到空气中，直到二者最终达到相同的温度。这时候你就完全没辙了——无论最初有多少热能，突然它就变得没用了，你没法利用它。要让马达再次启动，你需要重新建立温度梯度，但你没法轻轻按下一个开关，就指望温差自动出现。创造新的温差总是需要消耗能量的，这些能量必然来自另一个地方。最简单的做法是烧一壶水，再沏一杯茶，但这不是免费的。
有什么东西在夺走我们的能量。当然，这些能量没有被摧毁，只是无法再被利用。夺走它的是谁，或者是什么东西？如果一杯热茶被放得太久，是什么让茶水里的热量自发地离开了？是什么如此坚定地抹除了温差，让我们无法再汲取有用的能量？
答案是“熵”这个捕手。
借助焦耳和冯·梅耶的发现，德国物理学家兼数学家鲁道夫·克劳修斯（Rudolf Clausius）重新审视了卡诺的研究，弄清了这件事。熵是热转移的媒介，是能量被锁住的手段。克劳修斯称之为“转变容度”（transformation content）。这就是熵的含义。“entropy”这个词源自古希腊语中的“tropos”，它描述的是一个转变，或者说转折点，尤其是在战斗中。通过一些巧妙的数学方法，克劳修斯想出了一个将熵与它所捕获的能量联系起来的公式。他发现，熵会随着能量的变化而变化。此外，当整个系统处于低温状态时，熵对这种变化最敏感。 [3]
要弄清克劳修斯的公式在现实中如何起效，请想象一个靠热核爆炸供能的水壶和一种能承受极高温度的茶水。热核水壶会将茶水加热到超过太阳核心的温度，也就是1亿摄氏度左右。如果有10
-15
焦耳
的热量从茶壶散逸到周围的空气中，会发生什么？根据克劳修斯的公式，由于它损失了一部分热能，所以这壶茶的熵会降低一点点，差不多正好一个单位。而空气吸收了浪费的能量，所以它的熵会增加。问题在于，空气增加的熵是大于还是小于茶损失的一个单位？答案相当明确。空气应该比茶冷差不多100万倍（不然你的麻烦就大了）。因此，它的熵对能量变化的敏感程度应该高100万倍——空气的熵会增加近100万个单位。空气的熵增远大于茶的熵减。整个系统——茶和空气加起来——的熵必然增加。
这种熵增被称为热力学第二定律。它告诉我们，一个系统的总熵永远不会减少。有时候它会维持不变，但在这个动荡不安的现实物理世界里，熵倾向于增加，就像那杯超级烫的茶一样。正是因为存在这样的熵增，风车和汽车的发动机总会损失一点东西到周围的环境中。热力学第二定律甚至可以应用于整个宇宙，为我们提供一支时间之箭，熵永不休止的增长从过去指向未来。当我在镜子里发现一根灰色的头发时，我看到的正是这样的增长——这支射向未来的箭镞。它令我恐惧，不是因为我越来越老了，而是因为这对宇宙来说意味着什么。你看，随着宇宙的熵越来越大，它将越来越多的能量转化成了无用的热。它一点点吞噬我们的资源，削弱我们做功的能力，把越来越多有用的能量锁起来，就像一件越勒越紧的束身衣。未来是一场后熵时代的噩梦，谁都动弹不得。这是我们的热寂，宇宙被禁锢起来，不能动，什么都做不了。
克劳修斯解释了熵会做什么，但没解释 它是什么 。所以， 熵是什么 ？它和分身又有什么关系？要真正理解熵，我们需要更深入地研究工业革命的引擎——我们需要近距离观察里面的气体。
这些气体中几乎空无一物，原子和分子散落在广阔的空间里，如无头苍蝇般到处乱撞。你可以把它们想象成一群被关在空谷仓里的愤怒昆虫，这些虫子从一堵墙飞向另一堵墙，彼此碰撞，坠落又飞起，从左到右，从右到左，毫无章法地四处游荡。要描绘温度越来越高的气体，你可以想象这些苍蝇飞得越来越快。温度可以被理解为它们因为运动而拥有的平均动能——每个分子（在这里是指每只昆虫）携带的能量。有时这些昆虫会发生碰撞，在乱飞的过程中弹跳。它们撞上墙，或者别的什么东西，随心所欲，毫无规律，但碰撞产生的合力会被感知为压力。如果你站在谷仓里，它们会与你发生碰撞，你则会感受到它们的合力。如果我们把更多昆虫放进谷仓，它们会更频繁地碰撞你，而你感受到的撞击力会变大，压力也随之增长。随着谷仓里的虫子越来越多，这种压力会压垮你，摧毁你。这样的恐怖故事就发生在金星上，那里的气压是地球上的90倍。如果你发现自己身在金星，那里的空气分子会在瞬间把你挤压至死。
这套气体昆虫模型由丹尼尔·伯努利（Daniel Bernoulli）于1738年提出，这位天之骄子出生于瑞士一个科学和数学的贵族世家，他的父亲约翰和伯父雅各布是微积分和概率论的先驱。伯努利的模型让他能够根据分子的碰撞机制推导出描述压力和气体体积关系的玻意耳定律。尽管取得了这样的成功，以及在科学领域拥有崇高的地位，但伯努利的模型并不是特别受欢迎。18世纪，大多数科学家仍推崇热质模型，温度被定义为热质液体的密度。在他们眼里，伯努利把热当作一种锁在细小粒子微观运动中的能量形式来处理，实在没什么道理可言。毕竟，此时距离冯·梅耶的放血顿悟还有整整一个世纪。伯努利太超前于自己的时代了。
对伯努利来说更困难的是，他父亲试图窃取他的研究成果，约翰修改了自己手稿的日期，假装这些手稿比儿子的更早。约翰强烈的好胜心摧毁了这对父子的关系。1733年，他们共同获得巴黎科学院大奖的个人研究奖。对于这一折中处理，约翰火冒三丈，当即与儿子断绝了关系。
热质论终结于克劳修斯之手以后，丹尼尔·伯努利的才华终于有了施展的机会。这场复兴的见证者中有3个人尤其值得一提，他们分别是“电磁学宗师”麦克斯韦，低调的美国数学物理学家乔塞亚·威拉德·吉布斯（Josiah Willard Gibbs），以及最重要的路德维希·爱德华·玻尔兹曼（Ludwig Eduard Boltzmann），这位饱受精神折磨的天才最后以自杀的方式了结了自己的生命。
克劳修斯、麦克斯韦、玻尔兹曼、吉布斯等人开始将统计学方法应用于伯努利的模型。归根结底，气体中有大量随机运动的粒子，它们在空旷的空间中左冲右突。这些人证明了集体的现象将如何从微观的混沌中浮现出来。对气体来说，温度和压力宛如椋鸟群灵动变幻中优雅的投影，它埋藏在微观世界背后，但只要数量够多就会在宏观层面浮现出来。就温度而言，它可以被理解为分子的平均动能，以及这些能量如何随熵而变化——但熵本身呢？它又是什么？
熵是真正重要的东西。
我说真的。按照玻尔兹曼的解释，熵实际上是对微状态（microstate）的计数。微状态就像对宏观物体最终极的普查，它会告诉你这个宏观物体所有原子和分子的排布数据、它们在哪里，以及正在干什么。当我们考虑一定体积的气体、一颗鸡蛋，或者一头恐龙时，我们知道它由大量小微粒组成。每个原子都在这里或者那里，朝这个或那个方向旋转，以一定的速度掠过拥挤的狭小空间，这样的原子有成百上千亿个。当然，这些原子本身又有组成它的基本粒子，这些粒子有各自的内在属性。要完整地描述这些气体、这颗鸡蛋，或者这头恐龙，你可以写一张巨大的数据表（如果你疯了），列出这个系统中成万上兆亿个基本单元中每一个的位置、速度、自旋、喜欢的颜色、偏爱的组合和其他所有信息。这张表将描摹出一个特定的微状态，让你完整、精确地掌握该物品的所有信息。
但问题来了：如果你随便改变几个原子的位置，谁也不会注意到。蛋看起来还是那颗蛋，气体还是那个温度，恐龙也还是那头本应在6 500万年前就已灭绝了的三角龙。重点在于，看待宏观物体时，操心每一个最微小的细节是一件很蠢的事情。熵度量的就是这些隐藏的细节。它是所有微状态的总和，正是这些微状态共同赋予了一件稳定的物体的宏观特性。随着时间的流逝，蛋或者恐龙会崩解，化为尘埃，它越来越多的微观细节会被隐没。看着这堆残灰，你会越来越难以区分，这种可能的微状态和另一种有何不同。令人不安的是，对蛋或恐龙微状态的计数会随着时间的推移而增长。这就是熵增，一种只增不减的计数。
熵不一定总是关乎分子和原子。只要存在某种类型的微状态，我们就可以讨论它的熵，并对之进行计数。以面部识别软件为例。谢天谢地，哪怕有时候我的表情和第一次登录时不一样，我的手机还是能识别出来我。它剔除了所有冗余的数据，把我各种有微妙差别的照片识别为同一个人。要是你把所有这些全都加起来，就是对我的脸的熵的度量。
还有一个更量化的例子：英格兰足球超级联赛（简称英超联赛）由20支球队组成，一个赛季里每支球队会分别交手两次：主场和客场。所以每个赛季共有20×19=380场比赛，每场比赛有3种可能的结果——主场获胜，客场获胜，或者平局。这意味着一个赛季共有3 380 种可能的结果。不过，计算冠亚军和其他各支球队所获得的积分时，3 380 种结果中有很多种可以合并。我们可以把各种各样的结果视为微状态，如果赛季末的积分榜已经确定，我们就可以算出符合这个积分结果的所有胜负状态。这就是对英超联赛熵的度量。
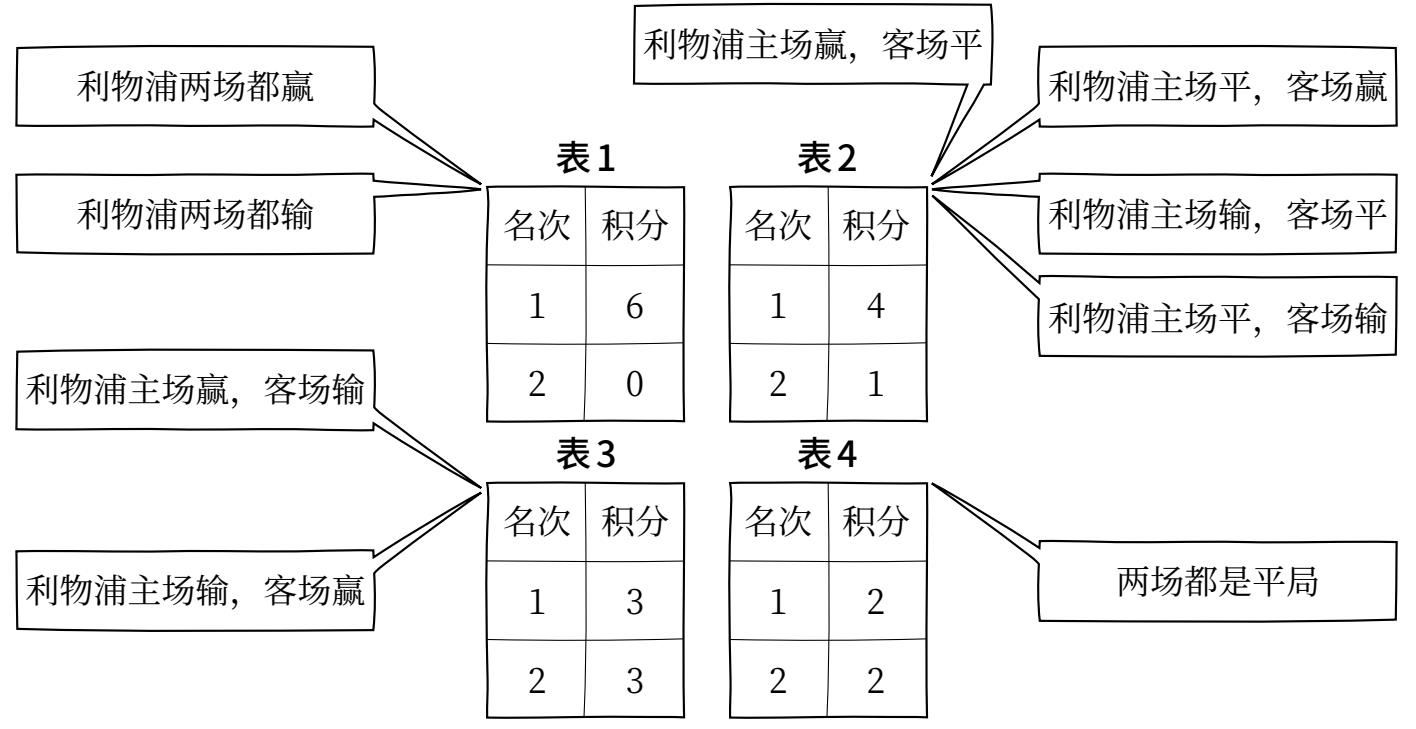
英超联赛共有20支球队，要详细审视所有细节实在过于痛苦，所以我们不妨削减数字，只留下联赛里两支最针锋相对的球队：利物浦和曼联。为了满足数学上的简化，其他所有球队都被抹除了，包括埃弗顿、阿森纳、马刺，甚至包括有石油资本撑腰的曼城。在这个缩水版的英超联赛里，一个赛季只有两场球要踢，因此共有9种可能的结果。如果我们决定忽略谁先谁后，有几种不同的结果可以被列入同一个联赛积分榜。记住，赢球得3分，平局得1分，输球不得分，那么4个积分表就足以囊括9种可能的结果，如下图所示。
我们仔细看看表1，冠军得6分，亚军得0分。要达成这个结果，有2种可能的方式：利物浦两场球都赢，或者两场都输。换句话说，同一个联赛积分表包含了两种截然不同的微状态。这样的计数赋予了表1的熵一个度量，或者更准确地说，这个度量来自它的自然对数。
我在这里迅速解释一下什么是对数。一个数的对数是它相对于某个底数的幂。例如，如果我们选择10作为底数，那么100的对数就是2，因为100是10的2次幂。 自然对数 通常写作“ln”，它的底数是 欧拉数 ， e ≈2.718，所以自然对数指的是e的几次幂。例如，ln e 2 =2，ln e 3 =3，ln e 0.12 =0.12……以此类推。在科学领域，自然对数比以10为底数的对数常见得多。
玻尔兹曼提出了一个自然对数形式的熵的方程S=ln W，其中W是对应的微状态数量，或者说有多少种 方式 。回到缩水版的英超联赛，表1和表3的熵都可以表达为ln2≈0.693，表2的熵是ln4≈1.386，表4的熵是0（因为ln1≈0）。讨论鸡蛋或者恐龙的时候，我们计算微状态和熵的方式也完全相同。唯一区别是所涉及的数字。能够描述你早饭吃的那颗蛋（或者恐龙！）的微状态数量非常多，多到要以古戈尔为量级，不像我们这个只有两支球队参赛的英超联赛，每张积分表对应的结果只有1种、2种或者4种。
现在，我们理解了英超联赛熵的概念，那它会怎么增长呢？其实很简单。假设这个赛季的结果是表1，它的熵是ln2。下一个赛季会发生什么？如果每个结果出现的概率完全相同，这个熵有4/9的概率依然是ln2（表1加表3），4/9的概率增加到ln4（表2），还有1/9的概率降低到0（表4）。因此，哪怕在这个尺度很小的例子里，熵增的概率仍远大于熵减。
如果我们把数字增大到古戈尔级，就像组成一颗蛋或者一头恐龙的原子数量那样，熵增将获得压倒性的胜利。熵增不再是一种可能性，而是 一种必然 。想象一下，将一块冰放在室温下。这个系统可以用冰的微状态来描述，随着时间的流逝，它会转移到其他可能的微状态。系统会在几种微状态间跳跃，最后你发现，它化成了一摊水，谁也不会感到意外。它仍是原封不动的一块冰的可能性非常小，但也不是完全不可能。在室温下，冰保持原状的微状态远少于化成水的微状态，这意味着冰融化的可能性占据压倒性的优势。熵的不断增长实际上只是混乱程度不可避免的上升。
我们也可以通过这些统计学游戏来理解热力学定律，能量成了“熵”这个狱卒的囚徒，宇宙走向瘫痪。重点在于，你积累的微状态越多，你对一颗蛋、一头恐龙或者一摊水的了解就被稀释得越厉害。从某种意义上说，窃取有用的能量变得更加困难，因为你无法确定它藏在哪里。这有点儿像一群贼试图偷走一件珍贵的珠宝，如果它被藏在一幢有成百上千个房间的豪宅里，他们很可能需要花很长时间才能找到它。如果这幢豪宅足够大，而这群盗贼在搜寻时又毫无章法，那么他们可能永远都找不到它。熵也如此，它把能量藏在一片混乱之中，让我们越来越难窃取它。玻尔兹曼明白，如果你任由事物自生自灭，它总会变得越来越混乱无序。花点儿时间看看新闻，听听我们的政客发言，你很快就会意识到玻尔兹曼是对的。
玻尔兹曼的工作真的很了不起。他不仅仅是无畏地从微观跳向宏观，从“小人国”跳进“大人国”。他还以强有力的数学为根基，搭建了一座桥梁，并清楚地展示了如何从上面安全通过。当然，和往常一样，他的想法遇到了一些阻力，因为不是每个人都准备好了接受原子的存在和真空的统治地位。面对这样的阻力，玻尔兹曼并没有做好万全的准备。他虽然才华横溢，但精神方面的问题很大，情绪时常大起大落，会做出一些疯狂的举动，或者陷入极度的抑郁。这个故事又以一个热力学悲剧结束。在的里雅斯特附近的杜伊诺，玻尔兹曼趁着妻子和女儿在海湾里游泳的时候，自缢身亡，没有留下任何遗书。让他走上这条绝路的是不是学术上的困境，我们无法知晓。我们只知道，在此前一年，爱因斯坦发表了一项最终让整个科学界相信原子存在的研究，并引领他们沿着玻尔兹曼搭建的桥梁走进了宏观世界，但是玻尔兹曼对此一无所知。 [4]
说回你和你的分身。和蛋、恐龙以及那些气体一样，你也由成百上千亿个原子和分子组成。我们不可能确切地知道这些原子的位置和行为。因此，要描述宏观世界里正在读这本书的你，适合的排列，或者说数据阵列，不止一种， 而是很多 。当然，还有其他很多微状态跟正在读这本书的你一点儿关系都没有。有的微状态描述了正在读《你好！》杂志的你，有的描述了一头正在读《你好！》的牛，有的描述了给定温度和压力下的一团气体分子，甚至有的微状态描述的只是真空本身。事实上，对你所占据的这片约1立方米的空间来说，我们可以想象出无数种不同的场景——各种有细微差别的不同版本的你、牛、气体或者真空。所以，从原则上说，要描述给定的任何1立方米的空间，可能的微状态必然有无数种，对吗？
不对。
这些微状态的数量是 有限的 。如果它们的数量是无限的，那么什么都无法阻挡这1立方米空间内的熵不断增长，从古戈尔到古戈尔普勒克斯，再到TREE（3），甚至更大。但有一样东西阻止了这种局面的出现：引力。克劳修斯告诉我们，熵和能量的增长是同步的；而爱因斯坦则告诉我们，能量有重量。如果你试图把太多的熵挤进1立方米的空间，引力会感受到随之增长的能量带来的重量，并召唤出那位“狱卒”。一个黑洞将不可避免地形成。
黑洞是熵的极限。它们比任何人、任何事物都更擅长掩藏自己的微观秘密。它们是面目模糊的果壳，你永远不会知道它们可怕的过去—— 永远无法知道 。当你望向它们并试图测量它们时，黑洞只会透露自己的3个参数：质量、电荷和自旋。除此以外的所有信息都秘而不宣。如果你在自家花园深处偶遇一个小黑洞，你知道它是怎么来的吗？如果第二天它还在那里，只是变重了，增加了大约一头大象的重量，你能确定它真的吞噬了一头大象吗？难道它就不会是吞噬了质量、电荷和角动量相当于一头大象的全套莎士比亚戏剧？这两种情况产生的黑洞完全相同，它们的质量、电荷和自旋没有任何区别，所以你怎么知道实际发生的是哪种情况？你怎么能知道这个黑洞的真实历史？
黑洞对秘密的守口如瓶暗示了它储存熵的无可匹敌的能力。黑洞的形成有许多种可能的途径，无论是来自大象还是来自莎士比亚的文本，这些信息都不会体现在它的宏观特征中。不管这些信息到底是什么，它们都散逸在许多种可能的宏观状态中。对一个给定体积的空间来说，任何事物蕴含的熵都比不上恰好能被这个空间容纳的黑洞，它的事件视界就等于这个空间的边界。但既然黑洞是熵的极限，那么它们到底蕴含了多少熵呢？
对大部分宏观物体来说，无论是鸡蛋还是人类或者恐龙，它们的熵都会随体积而增长，比如说如果一头三角龙妈妈在每个维度上都比它的宝宝大10倍，那么它拥有的熵差不多就是宝宝的1 000倍。这听起来很符合直觉，三角龙妈妈占据的体积是宝宝的1 000倍，因此这个空间内包含的原子数量也是后者的1 000倍。每一个原子都会引入一些新的可能性，比如该原子是朝这个方向还是那个方向自旋。每个新原子有2种可能性，100个新原子就有2 100 种可能性，100万个新原子就有2 1 000 000 种可能性，以此类推。显然，随着原子数量的增长，可能性的数量和微状态的数量都呈 指数式增长 。熵是微状态的对数——它取的是指数的幂，所以熵和原子的数量必然成 正比 。三角龙妈妈的熵就是比宝宝大1 000倍。
但三角龙不是衡量熵的典型事物。我们可以把10亿头三角龙挤进同样的空间里，创造出一个体积相同但熵比原来大得多的“三角龙罐头”。鸡蛋、人类和三角龙，他们都不接近熵食物链的顶端。但黑洞接近，正因如此，“黑洞妈妈”和“宝宝”蕴含的熵的比例和三角龙母子很不一样。黑洞的熵随事件视界的面积而增长，而不是体积。听起来完全反直觉，这只是因为我们还不习惯面对被引力挤压得这么厉害的物体。
20世纪70年代初，以色列裔美国物理学家雅各布·贝肯斯坦（Jacob Bekenstein）和与他旗鼓相当的英国科学家史蒂芬·霍金（Stephen Hawking）证明了面积为AH的黑洞拥有的熵等于：
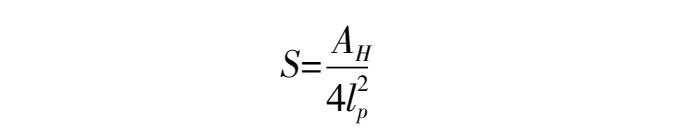
其中l p 这个符号代表普朗克长度 [1] 。这是物理学中最短的、有意义的长度，相当于10 -33 厘米。它对应的是我们对引力理解的极限——就是在这里，引力开始与量子力学主宰的微观世界眉来眼去，时空的经纬开始变得模糊，甚至可能断裂。
霍金利用一些巧妙的热力学论证确定了这个方程的细节，但仍缺乏适当的 微观 推导。我们真正想做的是取一个典型的黑洞，利用它的3个宏观特性（质量、电荷和自旋）确定与之对应的所有微状态。然后我们对这些微状态进行计数，看看由此算出的熵 是否完全吻合 贝肯斯坦和霍金的方程。目前还没人知道该如何做到这一点，至少对我们发现的在星系中央巡游的那些黑洞来说是这样的。 [5] 这个问题仍是黑洞研究领域的圣杯。
让我们回到恰好被你占据的这1立方米的空间，或者确切地说， 任何 1立方米的空间。要完全确定它所有可能的物理特性，你需要多少种微状态？要回答这个问题，我们需要考虑所有可能的微状态，逼近熵的极限。换句话说，我们需要考虑能被这个空间容纳的最大黑洞。这个黑洞的事件视界表面积应该约等于1平方米，因此，根据贝肯斯坦和霍金的方程， [6] 它的熵大约是10 69 ，差不多等于10 10 68 种微状态。这就是答案。这就是极限。这就是你描述1立方米空间最多需要的微状态的数量。
作为一个有抱负的大数字爱好者
，我要给这个大得超乎想象但有限的数字起一个名字：分身数（doppelgängion）。我们在这一章和下一章的交会处，古戈尔和古戈尔普勒克斯之间，找到了它。感觉很合适。毕竟，分身数正好介于这两个庞然巨数之间。它远大于古戈尔，又远小于古戈尔普勒克斯。要完全理解它的重要意义，我们需要继续深入下一章，寻找你的分身，从亚原子层面探索“你是你”这件事到底意味着什么。
多亏了熵的这种极限，现在我知道了，在我写下这些文字时，我所占据的这1立方米的空间至少能被10 10 68 种微状态中的一种描述。这同样适用于哈里王子和梅根·马克尔占据的1立方米空间，或者仙女座星云边缘正密谋发动一场跨星系战争的气态外星人所占据的1立方米空间，还有你。你存在的概率小于古戈尔分之一，但大于古戈尔普勒克斯分之一。我们每个人最多不过是分身数分之一。
也许我还是太善良了。从10 10 68 种微状态中选择，可能有好几种能够恰如其分地描述你和你的宏观特征——同样的鼻子、同样的耳朵、同样快活的表情等。你的分身大概也拥有同样的特征。如果想要更精确一点，我们可以试着进一步缩小相关的微状态范围。我们可以开始询问你体内每个原子的准确状态，或者你脑子里迸发思维火花的神经细胞的状态。这完全取决于我们想用什么样的精度定义你以及你的分身。你们必须相似到何种程度才能互为分身？是看起来像就够了，还是你们必须拥有同样的想法、同样的原子排列？无论如何，当你开始测量每个原子状态的那一刻，你就进入了微观世界，那个由量子力学主宰的世界，也是下一章的主角。寻找你的分身，这个任务从此变成了一趟量子征程。老实说，其实一直如此——宇宙是量子。 你是量子 。
你的分身也是。