




在第1章中,我们了解到机器学习模型面临的一个主要的挑战就是出现过拟合的现象。当然,线性模型也存在过拟合的风险。为了尽可能地解决这个问题,这一节我们就学习一下正则化技术。
要了解正则化的基本概念,我们可以在ChatGPT对话框中输入“什么是正则化”,得到如下答复。
ChatGPT正则化(Regularization)是机器学习中一种常用的方法,用于减小模型的过拟合风险,提高模型的泛化能力。过拟合是指模型在训练集上表现非常好,但在测试集上表现不佳的现象,可能是因为模型过于复杂,过度适应了训练集的噪声数据,而失去了对真实数据的泛化能力。
正则化通过在损失函数中增加正则化项(Regularization Term),对模型参数进行限制和约束,从而降低过拟合风险。正则化项一般为模型参数的平方和或绝对值之和,惩罚模型的复杂度,使模型更倾向于选择较为简单的参数值,避免过拟合。
常见的正则化方法包括L1正则化和L2正则化。L1正则化通过增加模型参数的绝对值之和进行约束,能够产生稀疏性,即将一部分参数置为零,从而产生稀疏模型;L2正则化通过增加模型参数的平方和进行约束,能够产生平滑性,即让参数值尽量接近零,从而产生平滑模型。在实际应用中,可以通过交叉验证等方法选择合适的正则化方法和参数,以获得更好的模型泛化能力和性能。
从上面的答复可以看到,正则化技术实际就是通过添加正则项约束模型的复杂度。那么有哪些线性模型使用了正则化技术呢?在ChatGPT对话框中输入“有哪些正则化线性模型”,会得到如下答复。
ChatGPT正则化线性模型是指在线性模型的基础上,增加正则化项进行约束的模型。常见的正则化线性模型包括以下几种。
1.岭回归(Ridge Regression):在普通最小二乘法的基础上增加L2正则化项,使模型参数更趋向于平滑,可以有效地降低过拟合风险。
2.Lasso回归(Least Absolute Shrinkage and Selection Operator Regression):在普通最小二乘法的基础上增加L1正则化项,使模型参数更趋向于稀疏,即可以使一些特征对模型的贡献变为零,从而进行特征选择。
3.Elastic Net回归:在普通最小二乘法的基础上同时增加L1和L2正则化项,综合了岭回归和Lasso回归的优点,既能平滑参数,又能进行特征选择。
4.Logistic回归(Logistic Regression):是一种广义线性模型,将线性模型的输出通过逻辑函数(Logistic Function)映射到[0,1]之间,表示某个样本属于某个类别的概率。可以通过增加L1或L2正则化项进行约束。
5.支持向量机(Support Vector Machine,SVM):通过最大化分类间隔(Margin)寻找决策边界,可以通过增加L2正则化项进行约束。
这些正则化线性模型得到了广泛应用,可以有效地提高模型的泛化能力和性能。
从上面的答复中可以看到,ChatGPT列举了一些常见的正则化线性模型,包括岭回归、Lasso回归(一般翻译为“套索回归”)、Elastic Net回归(一般翻译为“弹性网回归”)、Logistc回归(也就是我们前面学习的逻辑回归)及支持向量机。这里之所以把支持向量机也归入线性模型中,是因为它也支持使用线性内核。与支持向量机相关的知识在后面的章节中会详细讲解。
前面ChatGPT已经告诉我们,岭回归是使用L2正则化技术的线性模型。为了直观了解L2正则化给模型带来的影响,我们可以先用一个例子试验一下。在ChatGPT对话框中输入“用Python代码演示岭回归与线性回归的区别”,会得到如下答复。
ChatGPT下面是一个简单的示例,演示使用Python中的scikit-learn库实现岭回归和线性回归,并比较它们的性能差异。


运行代码后得到输出结果,可以发现岭回归模型的均方误差略小于线性回归模型的均方误差,说明在这个数据集上岭回归的表现更好一些。这是因为岭回归通过增加L2正则化项约束模型参数,使模型更趋向于平滑,可以有效地降低过拟合风险,从而提高模型的泛化能力。
在这段代码中,我们可以看到ChatGPT直接使用了scikit-learn库中内置的波士顿房价数据集,免去了我们下载数据集的工作。大部分代码我们在前面都已经讲解过,相信大家已经不再陌生。下面我们将代码直接粘贴到Jupyter Notebook中观察它的运行情况。为了能更加清晰地体现L2正则化的效果,我们可以把岭回归的alpha参数调高一些(这里调到100),代码运行结果如下。

从代码的运行结果可以看到,在将岭回归中用来控制正则化强度的alpha参数调到100时,岭回归的均方误差约为33.27,而没有使用正则化的线性回归模型的均方误差约为29.78。导致这种现象出现的原因就是我们使用了比较强的正则化项,将模型的参数进行了压缩。
我们可以通过下面的代码观察两个模型参数的对比。

运行上面这段代码,可以得到如图3-4所示的结果。
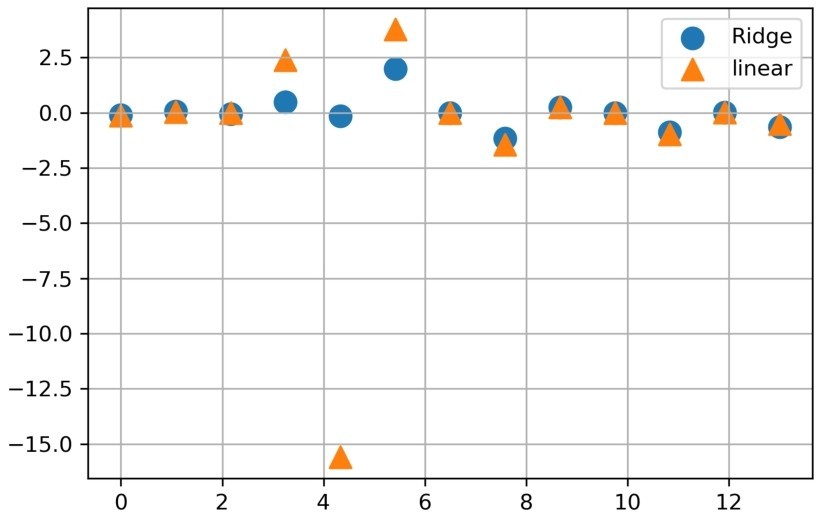
图3-4 线性回归与岭回归模型参数对比
在图3-4中,圆形是岭回归模型的参数,三角形是线性回归模型的参数。从图中可以比较清楚地看到,两个模型的样本第4、5、6个特征的参数差别是比较大的,尤其是第5个特征,被压缩的幅度是最大的。这说明我们添加的正则化项将这几个特征对模型的影响大大降低了。
在前面的小节中,我们学习了使用L2正则化的岭回归。可能很多读者会思考,L2正则化和L1正则化有什么区别呢?这是一个很好的问题,我们也可以让ChatGPT给出答案。在ChatGPT对话框中输入“L1正则化和L2正则化的区别”,会得到如下答复。
ChatGPT L1正则化和L2正则化都是用于控制机器学习模型过拟合的方法,但它们的惩罚项略有不同,因此在实践中也会有所不同。
L1正则化和L2正则化的惩罚项分别如下。
L1正则化:||w|| 1 =Σ|w i |
L2正则化:||w|| 2 =(Σ w i ^2)^1/2
其中,w表示模型的参数。
L1正则化和L2正则化的区别主要有以下几个方面。
1.惩罚项的不同:L1正则化使用绝对值作为惩罚项,而L2正则化使用平方和开根号作为惩罚项。
2.惩罚强度的不同:L1正则化和L2正则化的惩罚强度由正则化系数控制,但相同的正则化系数下,L1正则化会使模型更倾向于产生稀疏的参数(一些参数变为0),而L2正则化则会让所有参数都尽可能小,但不会使任何一个参数变为0。
3.对异常值的鲁棒性:L1正则化对异常值更为鲁棒,因为它使用绝对值作为惩罚项,而L2正则化对异常值更为敏感,因为它使用平方和作为惩罚项。
4.计算复杂度的不同:在计算复杂度上,L1正则化需要进行L1范数的计算,而L2正则化需要进行L2范数的计算。由于L2范数是平方和开根号,相对于L1范数来说,L2范数的计算更加复杂。
综上所述,L1正则化和L2正则化都是用于控制过拟合的有效方法,但它们的具体效果和应用场景有所不同。在实际应用中,我们可以根据具体的情况选择适合的正则化方法。
从ChatGPT的答复中可以看到,虽然L1正则化和L2正则化都是控制过拟合的方法,但两者的区别还是比较大的——两者的计算方法不同,因此模型的参数也有差异。比较明显的是,使用L1正则化的模型会出现参数为0的情况,也就是把一些特征彻底剔除;而使用L2正则化的模型则不会。
接下来我们让ChatGPT用例子演示使用L1正则化的模型,为了便于和前面的例子比较,我们规定ChatGPT仍然使用波士顿房价数据集。在ChatGPT对话框中输入“用波士顿房价数据集演示L1正则化的模型”,会得到如下答复。
ChatGPT使用波士顿房价数据集演示L1正则化的模型,可以帮助我们更好地理解L1正则化对机器学习模型的影响。下面是一个使用L1正则化的线性回归模型的示例。


在上述代码中,首先,我们使用load_boston函数加载了波士顿房价数据集,并将其拆分为训练集和测试集。然后,我们初始化了一个Lasso模型,并将正则化系数alpha设置为0.1。接着,我们使用训练集对模型进行训练,并输出了模型的系数和截距。最后,我们计算了模型在测试集上的均方误差,并绘制了模型的系数分布图。
通过输出模型的系数和截距,我们可以看到,L1正则化使模型的一些系数变为了0,从而实现了特征的稀疏化。此外,我们可以通过绘制模型的系数分布图更直观地观察模型的稀疏化效果。
值得注意的是,L1正则化可以帮助我们剔除一些不重要的特征,从而提高模型的泛化能力。但是,如果正则化系数设置得过大,可能会导致模型欠拟合。因此,在实践中,我们需要根据具体的情况选择适当的正则化系数。
下面我们从ChatGPT给出的代码中筛选有用的部分,稍加修改并进行试验。

上面这段代码使用Lasso回归模型进行了演示。为了充分展现L1正则化项的影响,我们把参数alpha修改为10,也就是更严格地抑制模型的参数。运行代码可以得到以下的结果。

从上面的代码运行结果中可以看到,经过L1正则化项的“压制”,模型的若干个参数的值都变成了0。也就是说,与之对应的样本特征被完全剔除了。
同样,我们可以用可视化的方法对比Lasso回归与岭回归模型的参数,使用的代码如下。


运行代码,会得到如图3-5所示的结果。
在图3-5中,节点为三角形的折线代表Lasso回归模型的参数,节点为正方形的折线代表岭回归模型的参数。通过对比,我们可以很直观地看到,Lasso回归的大部分参数值都比岭回归小,这在一定程度上解释了L1正则化与L2正则化的区别。
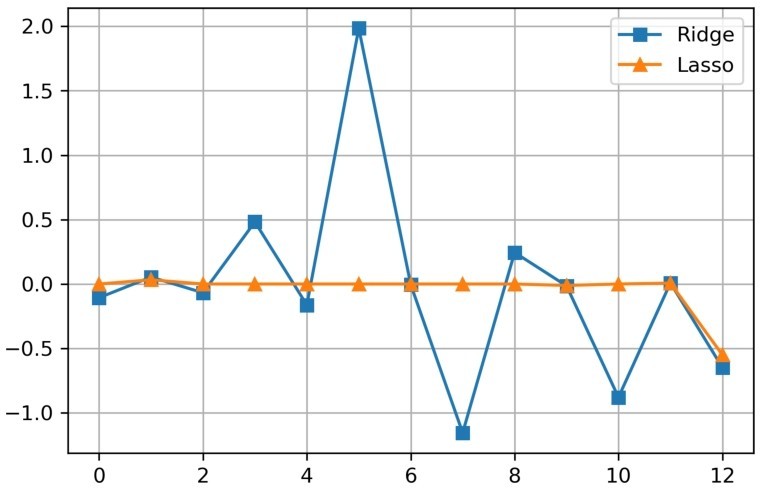
图3-5 Lasso回归与岭回归模型参数对比
本例只是为了演示两种正则化项对模型参数的影响,因此将控制正则化项的参数设置得比较高。在实际应用中,应该根据样本的情况酌情设制该参数,避免“矫枉过正”,使模型出现欠拟合的情况。