




为了弄清楚什么是线性模型,我们可以在ChatGPT对话框中输入“什么是线性模型”,会得到如下答复。
ChatGPT线性模型是一种用于建立输入变量与输出变量之间线性关系的统计模型。该模型的基本形式是一个线性方程,其中输出变量是输入变量的线性组合加上一个常数项。线性模型可以用于回归和分类问题,并且被广泛应用于统计学、机器学习和数据科学等领域。
常见的线性模型包括以下几种。
1.线性回归模型:用于预测连续型输出变量的值。
2.逻辑回归模型:用于预测二元分类问题的输出变量的值。
3.多项式回归模型:用于拟合高阶多项式函数的回归模型。
4.岭回归模型:用于处理多重共线性问题的回归模型。
5.Lasso回归模型:用于进行特征选择和稀疏化的回归模型。
6.线性判别分析模型:用于进行多类别分类的模型。
线性模型具有许多优点,如可解释性强、计算效率高等,但它们通常不适合用于非线性问题。
从初学者的视角看ChatGPT的答复,会觉得有些抽象。接下来我们就通过一些实例学习常用的线性模型。
为了能够更好地理解线性回归的原理,我们可以要求ChatGPT提供一个示例代码。在ChatGPT对话框中输入“线性模型的Python示例代码”,会看到ChatGPT给出的答复如下。
ChatGPT下面是一个使用Python实现线性回归模型的示例代码。


这段代码首先使用NumPy库准备了一组输入变量和输出变量,然后使用scikit-learn库中的LinearRegression类创建了一个线性回归模型对象,并使用fit()方法拟合了数据。接下来,使用predict()方法预测了一个新的输入变量,并输出了其对应的输出变量。最后,使用Matplotlib库绘制了回归线和原始数据点的散点图。
接下来,我们可以在Jupyter Notebook中新建一个Notebook文件,把ChatGPT生成的代码粘贴到单元格中并尝试运行。
下面我们逐步分析每段代码分别起什么作用。
上面这段代码导入了用于科学计算的NumPy库和绘制图像的Matplotlib库,同时还导入了在机器学习中非常常用的scikit-learn库中的线性回归模型LinearRegression。接下来的这段代码使用NumPy库生成了演示数据。

上面这段代码使用NumPy库的array函数生成了两个数组。其中作为特征的数组以x命名,作为目标值的数组以y命名。reshape()方法用于改变数组的形态。(-1,1)表示将数组转化为任意行,但只有1列的形态。
准备好数据后,我们可以尝试使用线性回归模型对数据进行拟合,也就是下面这段代码的作用。

运行上面的代码,模型会在一瞬间完成拟合,接下来就可以调用模型对新样本进行预测了。例如,新样本的x值是6,模型可以对它的y值进行预测,代码如下。

运行这段代码可以得到如下的结果。

从代码的运行结果可以看到,模型成功地对新样本的y值进行了预测。当新样本的x值为6时,模型预测出其y值为9.3。ChatGPT给出的代码还用图像直观地展示了模型的原理。

在这里,我们单独添加了一行用于控制图像大小的代码。同时使用Matplotlib库的scatter()函数绘制散点图,plot()函数绘制折线图。运行代码会得到如图3-1所示的结果。
在图3-1中,圆点是使用NumPy库生成的样本数据。例如,左下角的圆点就是我们生成的第一个样本,其x值等于1, y值等于2,以此类推。而图中的直线就是根据生成的样本拟合的线性回归模型。这条直线也很好地解释了“线性回归”名字的由来。
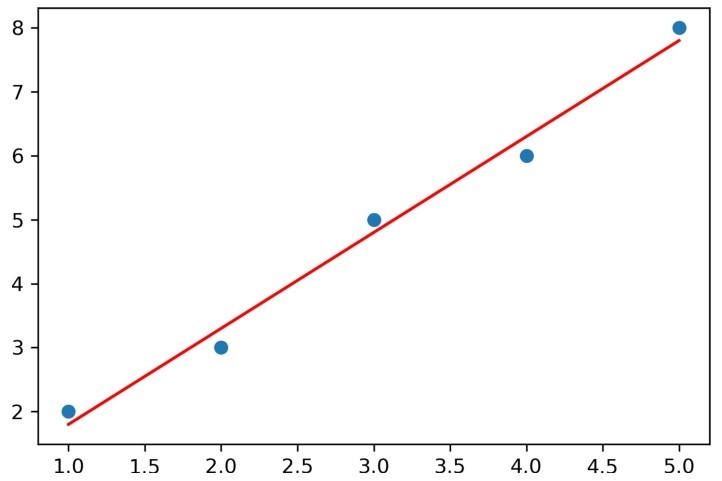
图3-1 用图像展示线性回归模型
在直观了解了线性回归模型后,我们还可以让ChatGPT介绍一下线性回归的原理。在ChatGPT对话框中输入“简单介绍线性回归的原理,不要Markdown格式”。这里我们强调让ChatGPT不要返回Markdown格式的文本,是为了让答复中不出现一些奇怪的符号。发送我们的要求,会得到如下答复。
ChatGPT线性回归是一种常见的机器学习算法,用于建立一个输入变量与输出变量之间的线性关系模型。其基本原理是通过找到最优的线性函数拟合已知数据的输入、输出关系。具体而言,线性回归通过最小化预测值与实际值之间的平方误差,找到最优的系数值,从而建立一个能够描述输入变量与输出变量之间线性关系的模型。该模型可以用于预测新的输入变量对应的输出变量。
线性回归模型可以表示为Y=b 0 +b 1 * X 1 +b 2 * X 2 +…+b n * X n +ε
其中,Y是输出变量,X 1 , X 2 ,…, X n 是输入变量,b 0 , b 1 , b 2 ,…, b n 是系数,ε是误差项。该模型通过寻找最优的系数值使预测值与实际值之间的平方误差最小。线性回归可以使用梯度下降等优化算法找到最优的系数值,从而得到一个可用于预测新的输出变量的模型。
结合ChatGPT的答复,我们可以更好地理解上面的示例。在本例中,我们的模型只有一个输入变量x,因此公式就可以表示为
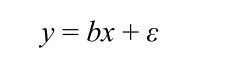
大家也许发现了,这其实就是一个直线方程。而模型在拟合的过程中,就是要找到最佳的系数b(对应直线的斜率)和误差项ε(对应直线的截距)。如果要查看这条直线的斜率和截距,我们可以让ChatGPT给我们示例。在ChatGPT对话框中输入“查看线性回归参数的Python代码”,会得到如下答复。
ChatGPT以下是使用Python的scikit-learn库中线性回归模型的参数查看代码。

在上面的代码中,我们首先导入scikit-learn库中的LinearRegression类;然后创建了一个名为model的线性回归模型对象;接下来用一些样本数据X和目标数据y训练模型;最后使用coef_和intercept_属性查看模型的系数和截距。其中,coef_属性存储了模型的系数值,intercept_属性存储了模型的截距。
从ChatGPT给出的代码可以看到,要查看线性回归模型的参数,只要使用模型的coef_属性和intercept_属性即可。我们在前面的例子中已经完成模型的拟合,因此只需要使用下面这两行代码即可。

把这两行代码粘贴到Jupyter Notebook中并运行,可以得到如下结果。

从上面的代码可以看到,我们训练的线性回归模型方程大致可以表示为y=1.5x+0.3。因此当我们给出x值为6时,模型就可以计算出y值为1.5×6+0.3=9.3。当然,如果我们有多个输入变量,模型就不再是一条直线,而是一个超平面了。
看到这里,可能有些读者会问:模型是如何确定最优的斜率和截距的呢?根据前面ChatGPT的答复,我们得知线性回归可以使用梯度下降等优化算法找到最优的系数值。那么,梯度下降是什么意思呢?这个问题我们也交给ChatGPT来回答。在ChatGPT对话框中输入“什么是梯度下降”,会得到如下答复。
ChatGPT梯度下降(Gradient Descent)是一种优化算法,用于最小化某个函数的值,这个函数通常被称为损失函数(Loss Function)。在机器学习和深度学习中,梯度下降被广泛应用于模型训练中,通过不断地调整模型参数,使损失函数的值逐渐降低,最终得到一个较优的模型。
梯度下降的基本思想是,通过计算损失函数对于模型参数的偏导数(梯度),沿着梯度的反方向更新模型参数,使损失函数的值不断降低。这个过程可以用数学公式表示为
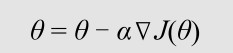
其中,θ表示模型参数,J(θ)表示损失函数,∇J(θ)表示损失函数对于θ的梯度,α表示学习率,即每次更新参数的步长大小。
梯度下降有两种主要的实现方式,分别是批量梯度下降(Batch Gradient Descent)和随机梯度下降(Stochastic Gradient Descent)。批量梯度下降每次更新模型参数时使用所有训练样本的梯度,因此计算量较大,但更新方向较为准确,可以保证收敛到全局最优解。而随机梯度下降每次更新模型参数时仅使用一个训练样本的梯度,因此计算量较小,但更新方向较为不准确,可能会收敛局部最优解。
除了批量梯度下降和随机梯度下降,还有一种折中的方式,称为小批量梯度下降(Mini-batch Gradient Descent),它每次更新模型参数时使用一小批训练样本的梯度,既可以保证更新方向比随机梯度下降更准确,又可以减少计算量,是目前最常用的梯度下降算法之一。
接下来还可以让ChatGPT用示例代码帮助我们更好地理解梯度下降的概念。在ChatGPT对话框中输入“用Python代码演示线性回归中的梯度下降”,可以得到如下答复。
ChatGPT下面是一个使用梯度下降算法进行线性回归的Python代码演示。


这段代码生成了一些随机的线性数据,然后使用梯度下降算法训练线性回归模型,并绘制了数据散点图和拟合的直线。在代码中,我们首先定义了损失函数和梯度函数,然后初始化模型参数,设置学习率和迭代次数,最后执行了梯度下降算法的循环过程。在每次循环中,我们计算损失函数和梯度,并使用学习率和梯度更新模型参数。最终,我们得到了最优的模型参数,并使用这些参数绘制了拟合的直线。
下面我们把代码粘贴到Jupyter Notebook中,并分段运行。首先是构造数据的部分。

在这段代码中,先使用NumPy库的linspace()生成了范围为0~10,数量为100的等差数列,作为样本的输入变量。然后将符合正态分布的随机数作为噪声添加到输出变量y。
接下来是定义损失函数和梯度函数的代码。

上面的代码先将输入变量x与参数矩阵theta相乘,得到输出变量y的预测值y_pred,再用全部预测值y_pred与真实值y的差的平方求均值,得到损失函数的值。然后用预测值y_pred和真实值y的差与输入变量x进行矩阵相乘,再除以样本的数量,得到梯度函数的值。
下面就可以用损失函数和梯度函数执行梯度下降算法了。
上面的代码使用NumPy库的zero()指定初始的参数theta为0,然后设置迭代次数为1000次,每次迭代都根据损失函数和学习率更新参数,并且让程序每经过100次迭代就打印模型的损失函数和最新的参数。运行代码,可以得到如下结果。

从代码运行的结果中可以看到,模型最初的损失函数约为69.2;而经过100次迭代后,损失函数降低到约1.1,此时的参数也变成了[0.55028868 2.0848709 ];此后损失函数不断降低,经过900次迭代后,损失函数降低到约0.9,而此时的参数已经更新为[1.25079686 1.97954236]。
最后,ChatGPT还用可视化的方式展示了最终的模型。

运行代码,可以得到如图3-2所示的结果。
这次我们没有使用scikit-learn库中内置的线性回归模型,而是通过自己定义损失函数和梯度函数的方式,使用梯度下降算法拟合一个线性回归模型。图3-2中的圆点是我们构造的样本数据,而直线是经过若干次迭代后,梯度下降算法找到的对数据拟合最好的线性回归模型。这个过程很好地解释了线性回归模型是如何找到最优参数组合的。
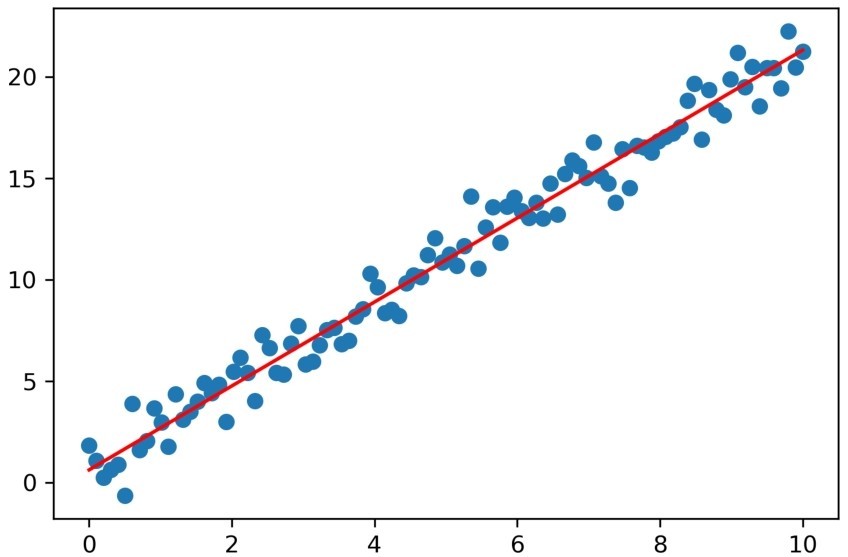
图3-2 使用梯度下降算法得到的线性回归模型
上面的代码主要是为了帮助大家理解线性回归模型通过梯度下降算法找到最优参数的过程。如果初学者在阅读代码的过程中感觉吃力也不要紧张,这部分代码并不要求大家掌握。