




简要阐述家庭照明电路的控制特点?家庭照明电路中所用到的电气元器件有哪些?各起什么作用?如何使用这些元器件?元器件上面的参数表示什么意思?
家庭照明电路中有些灯是单控的,如厨房灯;也有些灯是双控的,如走廊灯和卧室灯。根据使用要求设计家庭照明电路,分析各元器件在电路中所起的作用,绘制电路模型,简述其工作过程。
如图2-1所示,现有一个220V的单相交流电源、一个单相电能表、一个低压断路器、一个双控开关、一个荧光灯、导线若干,根据所给元器件设计由双控开关控制荧光灯亮灭的电路,要求该电路能计算用电量。
1)图2-2中AC 220V电源中AC的含义是什么?220V指的是什么值?符号L和N各表示什么?完成表2-1。
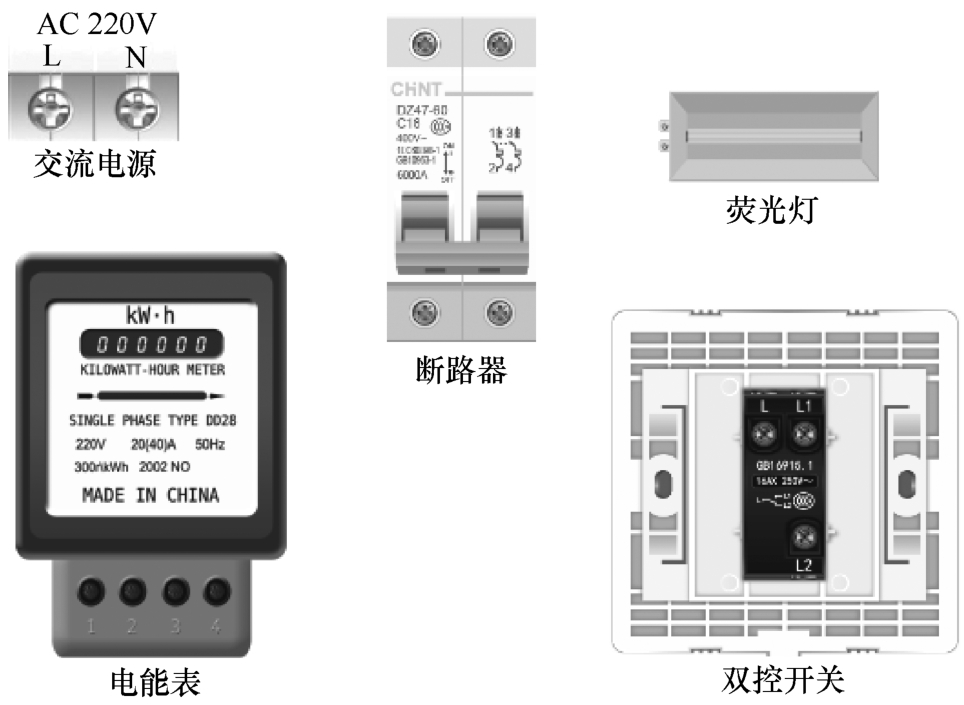
图2-1 家庭照明电路元器件图

图2-2 交流电源示意图
表2-1 交流电源参数

2)正弦交流电参数的表示方式有哪些?分别包含哪些要素?完成表2-2(以正弦交流电压为例)。
表2-2 正弦交流电压的表示法及其要素

3)假设图2-2中的交流电源的初相角为0°,用瞬时值表示法和相量表示法写出该交流电源的表达式(见表2-3)。
表2-3 220V正弦交流电源的表示法

4)图2-3为双控开关的内部接线端子示意图,实际使用中如何进行接线?哪个端子相当于COM端?L、L1、L2三个端子共有几种组合状态?
______________________________
5)图2-4为单相电能表示意图,电能表的作用是什么?在线路中四个端子如何接线?电能表的参数有哪些?各参数的含义是什么?完成表2-4。
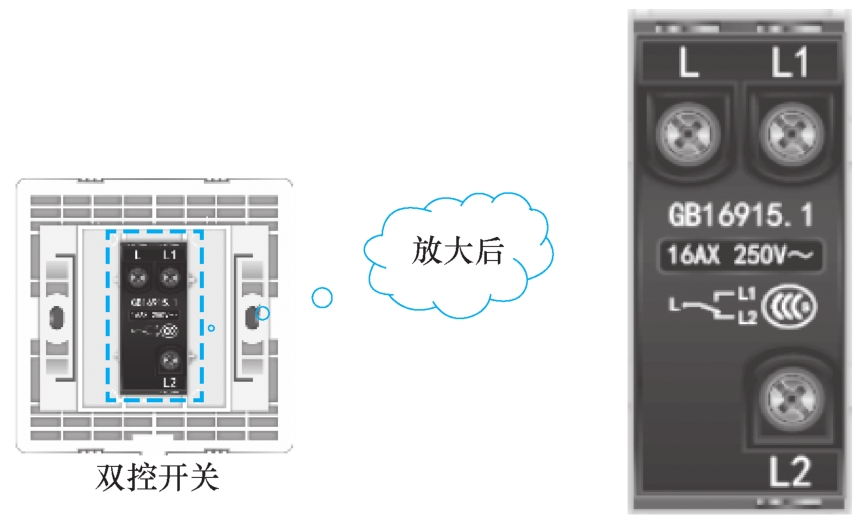
图2-3 双控开关接线端子示意图
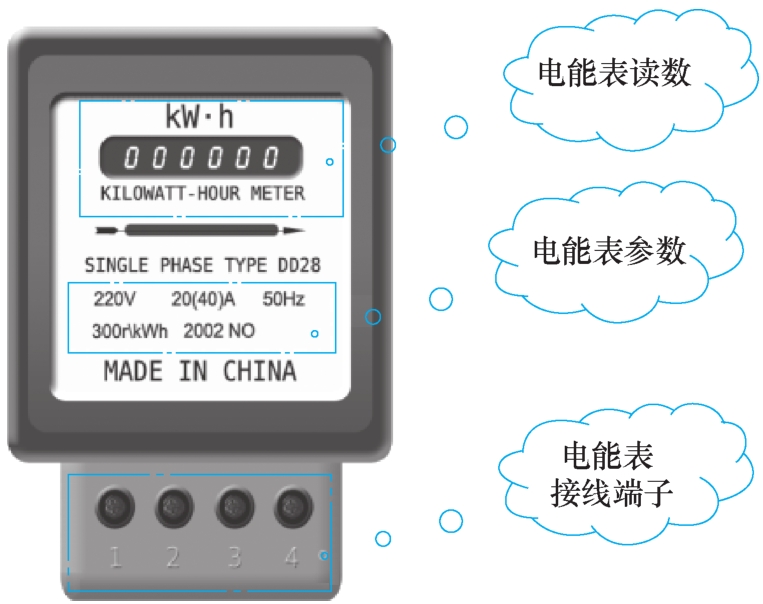
图2-4 单相电能表示意图
表2-4 电能表相关信息
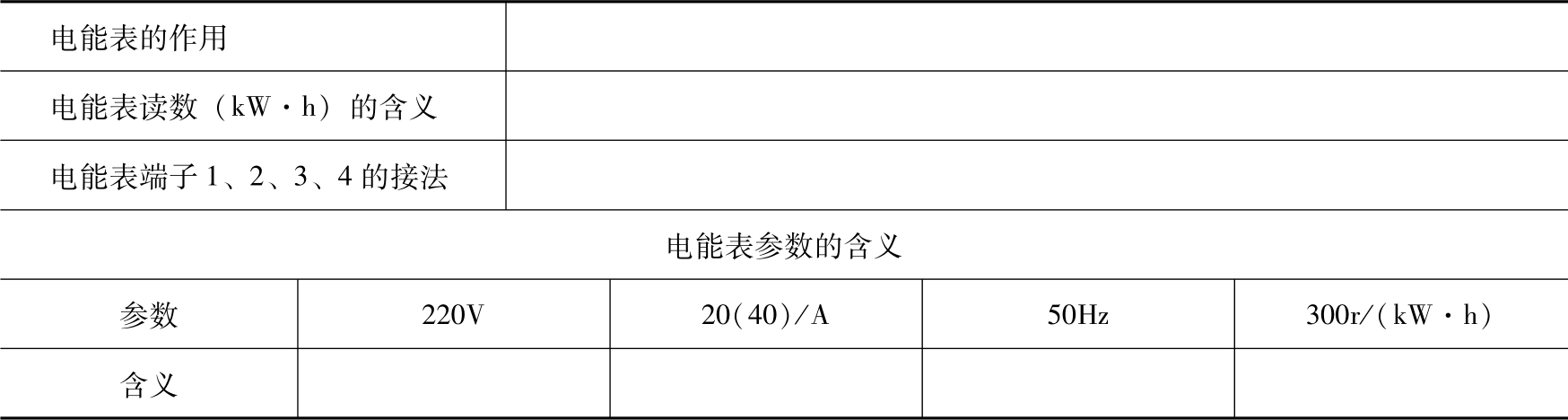
6)请根据图2-1将各元器件的功用填入表2-5中。
表2-5 双控开关控制荧光灯电路中各元器件的功用

7)根据图2-1所给的元器件设计家庭照明电路,要求用双控开关控制荧光灯的亮和灭,并用单相电流表测其使用的电能,在图2-1中用导线正确连接各元器件,注意横平竖直的布线方式。
8)荧光灯中的灯管和整流器用理想化的元器件模型来等效,填入表2-6,将荧光灯的电路模型绘制在图2-5中。
表2-6 荧光灯中灯管和整流器的等效元件


图2-5 荧光灯电路模型
9)简述荧光灯亮灭控制电路的工作过程。
______________________________
电路中输送电能和传递电信号的电流和电压,就其对时间的变化规律来看,主要分为两大类:一类是直流电,其大小和方向相对时间都不改变,项目一中描述的即为直流电;另一类是交流电,其大小和方向都随时间按某种规律变化。在交流电路中,应用最广泛的是正弦交流电,正弦交流电能获得广泛应用,其原因主要有几点:第一,正弦交流电易于产生、传输和转换,从而具有成本低廉的优势;第二,用电设备方面,由三相交流电源供电的三相异步电动机结构简单、价格便宜、使用维护方便,是使用最多的动力设备;第三,在需要使用直流电的地方,利用整流设备可以方便地将交流电转换为直流电;第四,正弦交流电便于计算,因为同频率的正弦量相加减或对时间的导数和积分仍是同频率的正弦量。本项目中所提到的交流电和交流电路都是指正弦交流电和正弦交流电路。
正弦交流电的数值随时间按照正弦规律变化,其波形能够直接在示波器上显示出来。
在分析计算正弦交流电路时,首先要假定正弦交流电的参考方向。在图2-6a所示的电路中,正弦电流 i 的参考方向用箭头标示。相应的电流波形如图2-6b所示,在波形的 正半周, i 是正值,表明这时电流的实际方向与图示参考方向一致; 反之,在波形的 负半周, i 是负值,表明这时电流的实际方向与图示参考方向相反。 与波形图相对应,该正弦电流的数学表达式为

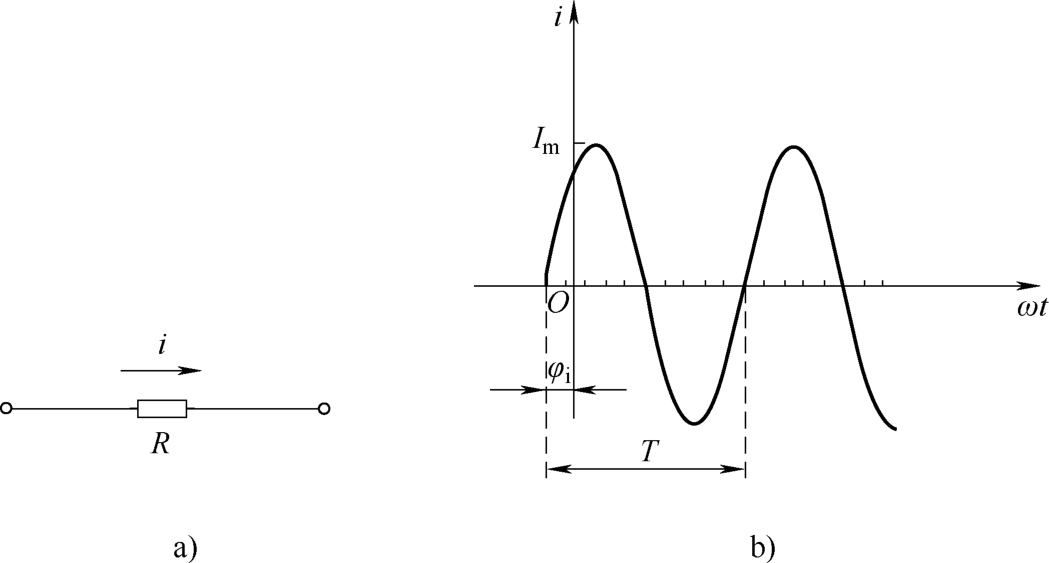
图2-6 正弦交流电流的参考方向和波形
正弦电量随时间按正弦规律变化。其在每一瞬时的数值称为 瞬时值 ,规定用 英文小写字母 i 、 u 、 e 分别表示正弦电流、正弦电压、正弦电动势的 瞬时值 。式(2-1)就是正弦电流的瞬时值表达式,该式表明一个正弦电量随时间变化的特征是由三个物理量决定的:最大值 I m 、角频率 ω 和初相角 φ i 。这三个物理量通常又被称为正弦电量的三要素。下面来分析正弦电量的三要素的特征。
(1)最大值和有效值
正弦电量瞬时值中的 最大数值 就称为 最大值 ,又称 峰值、振幅值 等,用 带下标m的大写字母来 表示。对于一个确定的正弦电量,其最大值为常数,表示正弦电量数值大小的特征。
在工程实际应用中,为了直接反映 交流电量的作用效果 ,更常用的是使用 有效值 表示交流电量的大小,用 大写字母 表示。
什么是交流电量的有效值?所谓有效值就是使一个交流电量的做功与一个确定大小的直流电量的做功相等,这个直流电量的数值就是该交流电量的有效值。因此,可根据 电流的热效应 ,对交流电量的有效值定义如下:交流电流 i 和直流电流 I 分别流过电阻值相同的电阻 R ,如果在交流电流一个周期时间间隔 T 内,两者产生的热量相等,即热效应相同,则该直流电流的数值 I 就是交流电流 i 的有效值,其表达式为

则有效值的表达式为

式(2-3)表明,交流电的有效值是瞬时值的方均根值。
当周期电流为正弦交流电时,即 i = I m sin ωt ,则可得

同理可得,正弦交流电压和正弦交流电动势的有效值分别是


在实际应用中所说交流电量的数值一般都是指有效值,如民用交流电的电压220V、低压动力用电的电压380V,其相应的最大值分别是311V和537V。交流仪表指示的数据一般也是有效值。
(2)周期、频率和角频率
周期、频率和角频率都是 表示正弦电量随时间变化快慢的物理量 。正弦电量随时间变化一周所经历的时间称为 周期 ,用大写字母 T 表示,单位是秒(s)。正弦电量在每秒时间内重复变化的周期数称为 频率 ,用小写字母 f 表示,单位是赫[兹](Hz)。假设正弦电量1s内变化一个周期,则其频率就是1Hz。
周期与频率互为倒数,有

我国发电厂提供的交流电能的频率是 f =50Hz,其周期是 T =0.02s。这一频率称为工业标准频率,简称工频。在其他工程技术领域还使用着不同频率的交流电,如电热技术中的中频电炉使用的频率是500~8000Hz、高频电炉使用的频率是200~300kHz、无线电技术使用的频率范围大致是10 5 ~3×10 11 Hz等。
正弦电量随时间变化的快慢还可以用 角频率 ω 表示。正弦电量变化一个周期对应变化了2π个弧度,角频率 ω 就是正弦电量在1s内变化的角度。

角频率 ω 的单位是弧度/秒(rad/s)。工频交流电的角频率是 ω =100π rad/s=314rad/s。为了避免和机械角度混淆,通常把正弦电量随时间变化的角度称为 电角度 。因此,角频率又称为电角频率或电角速度。
在交流电量的波形图中,其横坐标轴(时间轴)既可以用时间( t )标注,也可以用电角度( ωt )标注,波形图如图2-7所示。
(3)初相角
以正弦电流为例,其最大值 I m 和角频率 ω 确定之后,正弦电量随时间变化的进程就由它的电角度( ωt + φ i )确定。所谓随时间变化的进程就是正弦电量随时间变化到任一时刻 t 1 ,在时间轴上为一确定点,并决定了该时刻正弦量的 状态: 正、负值,数值大小和变化趋势 。如图2-8所示, t = t 1 时,对应波形的A点,该点瞬时值 i ( t 1 )>0,为正;数值大小由其在纵轴上的截距决定,数值变化趋势是数值增加。正是电角度( ωt + φ )确定了正弦电量随时间变化的进程,决定了正弦电量的状态,因此称 ωt + φ 为相位角,简称相位。
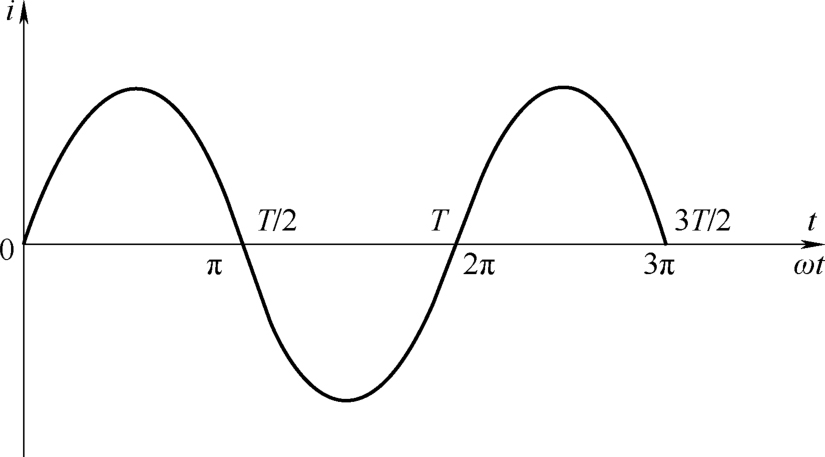
图2-7 波形图时间轴的标注
初相角 φ 是正弦电量在 计时起点 ( t =0)时,所对应的电角度,称为 初相角 ,又称初相位,简称初相,它决定了 t =0时正弦电量的状态。由于正弦电量在任意时刻的相位角( ωt + φ )都与初相角 φ 有关,所以初相角 φ 成为正弦电量的三要素之一。以图2-9为例,该正弦电流 i 的初相角 φ i ,它决定了 t =0时 i 状态,包含其数值 i (0)= I m sin φ i ,是正值,以及变化趋势为数值增加。
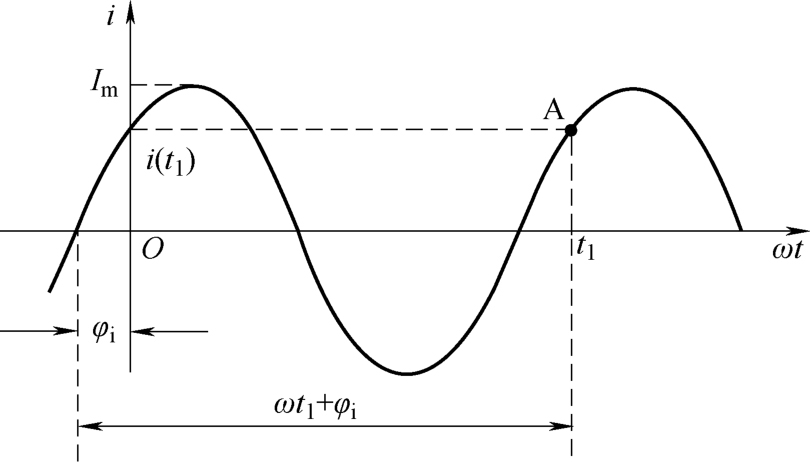
图2-8 正弦电量的相位角
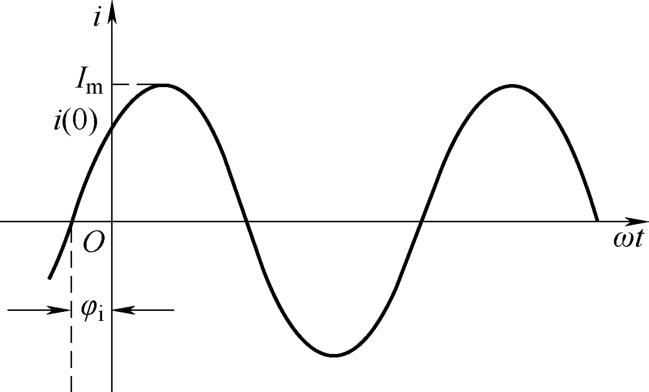
图2-9 正弦电量的初相角
初相角 φ i 与计时起点( t =0)有关,而计时起点是人为选取的。图2-9所示的情况是 φ i >0,为正值, i (0)>0。
图2-10a所表示的情况是 φ i <0,为负值,这时 i (0)<0。图2-10b所示的情况是的 φ i =0,这时 认为 i (0)=0。
由于正弦电量是周期性变化的,特规定初相角在绝对值小于π的主值范围内选取,即| φ |≤π。
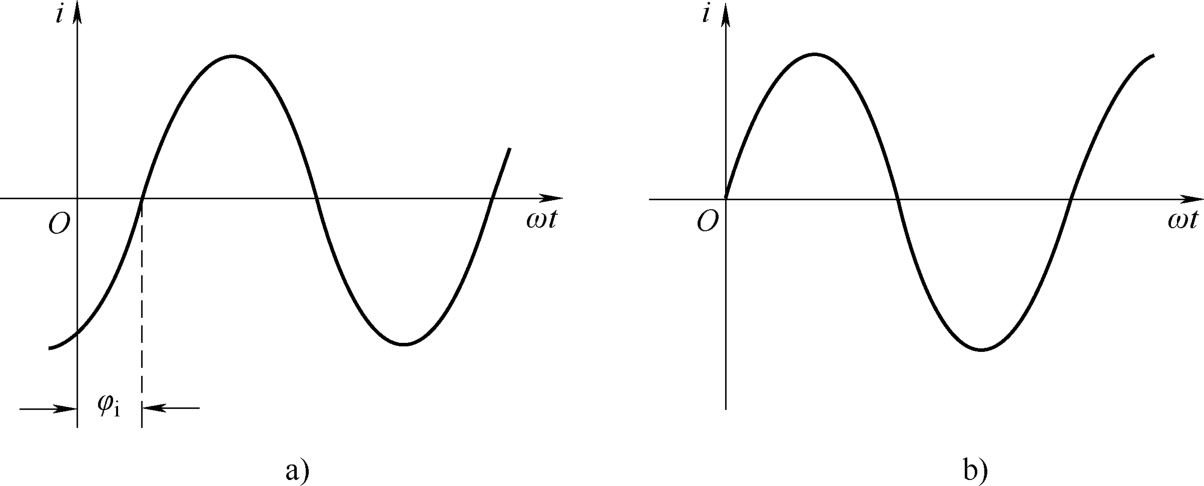
图2-10 初相角与计时起点的关系
在线性交流电路中,若所有电源的频率相同,则各支路的电流、电压也都是同频率的正弦电量,但是,它们随时间变化的进程往往不一样,也就是随时间变化的进程有先有后。为了描述 同频率正弦交流电量随时间变化的先后顺序 ,引入了相位差的概念。
什么是相位差呢?两个 同频率 正弦电量的相位角之差称为 相位差 ,用字母 φ 表示。例如,正弦电压 u = U m sin( ωt + φ u ),正弦电流 i = I m sin( ωt + φ i ),则同频率正弦电压 u 与电流 i 之间的相位差 φ 由式(2-9)决定:

由式(2-9)可知,两个同频率正弦电量的相位差 φ 就等于它们的 初相位之差 。
相位差有以下几种情况:
1)当 φ u > φ i 时,相位差 φ = φ u -φ i >0,此时 u 的变化进程领先于 i 一个 φ 角。 u 总是比 i 先通过零点达到正最大值,且领先的角度保持为相位差 φ 。这种情况称为 u 超前于 i ,或 i 滞后于 u 。波形如图2-11a所示。
2)当 φ u < φ i 时,相位差 φ = φ u -φ i <0,此时 u 的变化进程滞后于 i 一个 φ 角,或 i 超前于 u 一个 φ 角。波形如图2-11b所示。
3)当 φ u = φ i 时,相位差 φ = φ u -φ i =0,此时 u 的变化进程与 i 保持一致,称为 u 与 i 同相。波形如图2-11c所示。
4)当相位差 φ = φ u -φ i =±π,此时 u 与 i 相位相反,称为反相。波形图如图2-11d所示。
在描述相位差时,要说明哪个变量超前(滞后)于另一变量多少度。当选择的计时起点不同时,正弦电量的初相不同,但两个同频率正弦电量的相位差与计时起点无关。
需要注意的是, 不同频率正弦电量之间没有确定的相位差 ,也无法比较它们之间的超前、滞后关系。因此,它们之间不存在相位差问题。
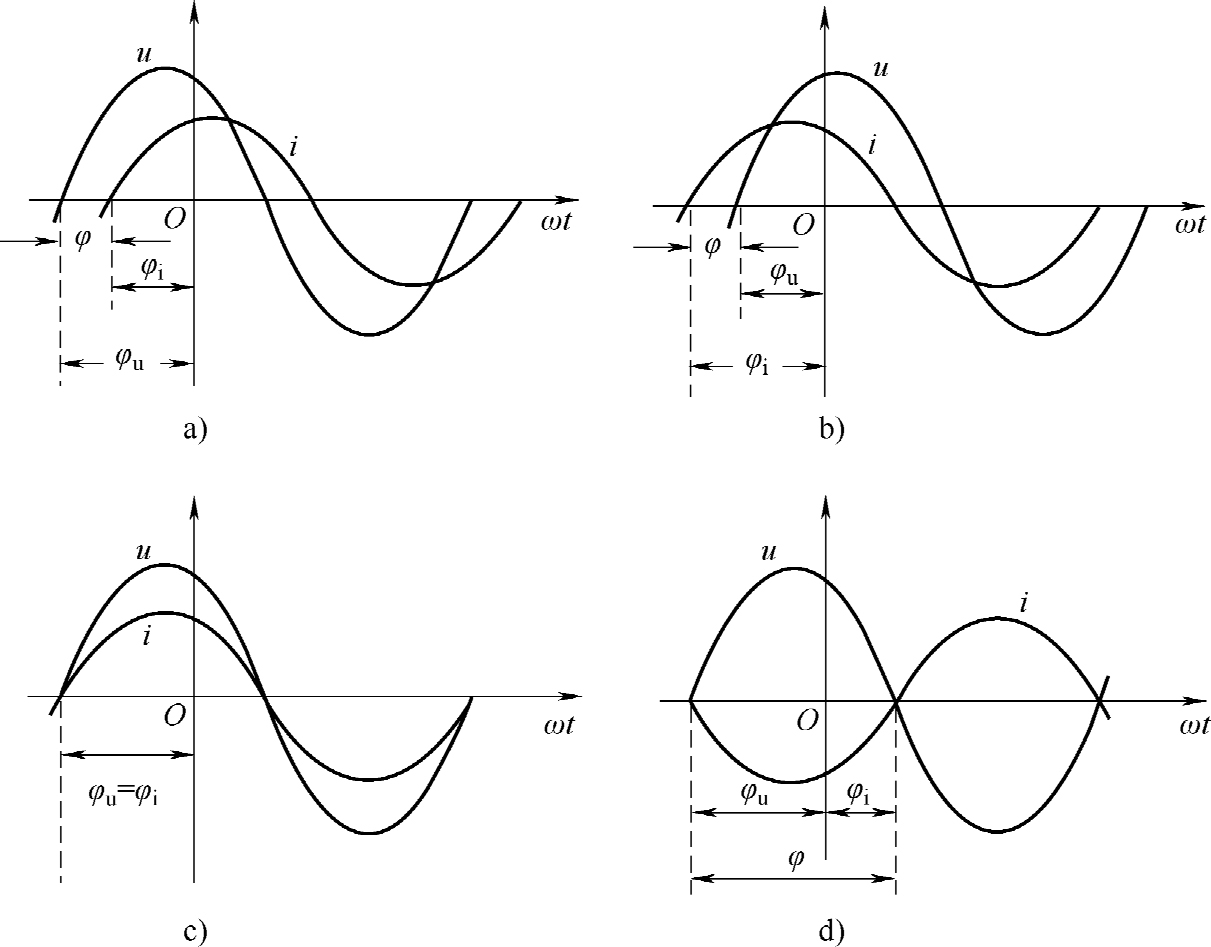
图2-11 同频率正弦电量的相位差
瞬时值表示式(也称三角函数式)和波形图是表示正弦电量随时间变化规律的基本形式。但是用这两种形式进行正弦电路的分析、计算则十分烦琐,很不方便。为此,有必要找到一种便于分析、计算的表示正弦电量的数学形式,这就是正弦电量的相量表示法。
相量表示法就是用复数表示正弦电量,并以此为基础形成在电路理论中被广泛应用的相量计算法。
在学习相量之前,先简要了解复数及复数运算的基本知识。
一个复数 A 是由 实部 和 虚部 组成的,如

这就是复数的
代数形式
。其中,
a
是复数的实部,
b
是复数的虚部,
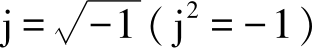 ,j是虚数单位。
,j是虚数单位。
在复数坐标平面上,复数 A 与一个确定的点相对应。该点在实数轴(横轴)和虚数轴(纵轴)上的投影分别是 a 和 b ,如图2-12所示。
如果用有向线段把坐标原点 O 和该确定点 A 连接起来,在线段末端加上带箭头的符号,则该有向线段成为一个矢量。该矢量就与复数 A 对应,称为 复数矢量 。式(2-10)又称为复数的 直角坐标形式 。
由图2-12可知,矢量模为

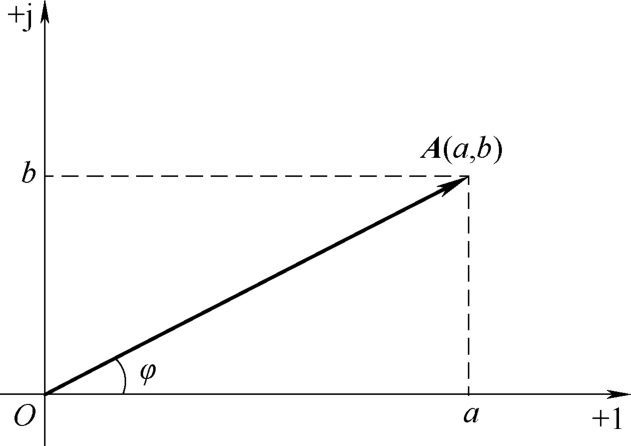
图2-12 复数矢量
矢量与 实数轴 的夹角称为 辐角

复数的实部 a 和虚部 b 与矢量模 A 和辐角 φ 之间的转换关系为
实部: a =| A |cos φ
虚部: b =| A |sin φ
将实部 a 和虚部 b 代入式(2-10),得

式(2-13)称为复数的三角函数形式。
根据高等数学中的欧拉公式,可以将复数的指数形式写成

在电路计算中,为了简化书写,常把上述复数的指数形式写成

A =| A |∠ φ 称为复数的 极坐标形式 。
假设有两个复数,即

(1)加、减运算
复数的加、减运算用 代数形式 进行,方法是 实部和虚部分别相加(相减) 。

(2)乘、除运算
复数的乘除运算用 极坐标形式 进行。
乘运算是 模相乘,辐角相加 。
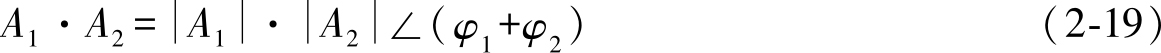
除运算是 模相除,辐角相减 。

复数乘以一个+j或-j是复数乘法运算的特例,首先,将+j和-j转换为极坐标的形式,有

那么,复数 A 乘以+j有
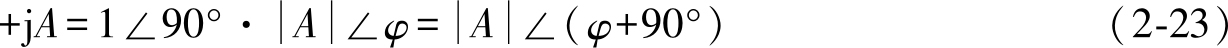
以上计算表明,任意一个复数 A 乘以+j,其模不变,辐角增加90°,对应的矢量逆时针方向旋转90°,如图2-13所示。
复数 A 乘以-j,有
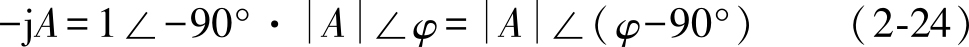
以上计算表明,任意一个复数 A 乘以-j,其模不变,辐角减小90°,对应的矢量顺时针方向旋转90°。因此,j被称为旋转90°的算子。
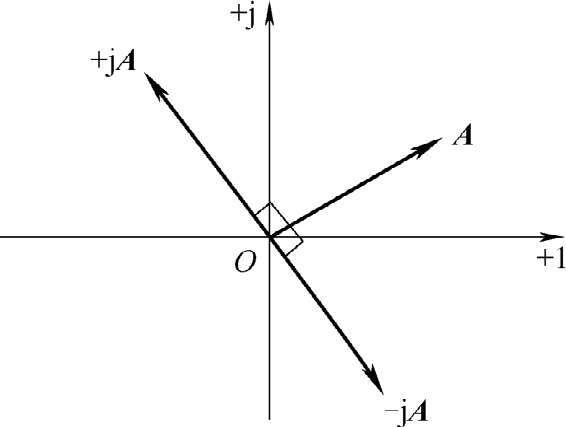
图2-13 复数 A 乘以±j
通过前面的学习可知,在线性正弦交流电路中所涉及的正弦电量都是同频率的正弦电量,因此,在求解未知正弦电量时,只需确定其 最大值(有效值) 和 初相角 就可以了,而这两个特征量可以用直角坐标平面上的一个 矢量 表示。
假设有一正弦电压 u = U m sin( ωt + φ u ),在 t =0时, u (0)= U m sin φ u 。如图2-14所示,在直角坐标平面上画一个矢量,它的模等于正弦电压的最大值 U m ,矢量与横轴的夹角等于正弦电压的初相角 φ u ,则该矢量在纵轴上的投影就等于此时正弦电压的数值 u (0)= U m sin φ u 。
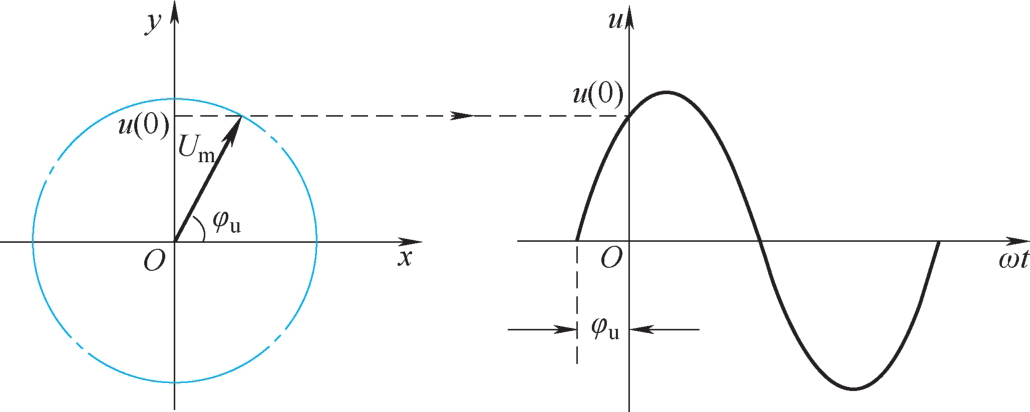
图2-14 用矢量表示正弦电量的最大值和初相角
由于一个正弦电量的最大值和初相角能够用矢量表示,而矢量又可以用复数表示。那么,正弦电量的最大值和初相角也必然能够用复数表示,这就是为什么正弦电量能用相量来表示的原因。
仍以上面的正弦电压为例, t =0时,对应矢量的复数表示式是

由于在工程实践中大多使用有效值表示正弦电量的大小,因此,用有效值代替最大值来表示复数的模,有

把这种表示正弦电量有效值和初相角的复数称为
有效值相量
,简称
相量
,并在电量的大写字母正上方加“·”,以便与普通复数进行区别。而式(2-25)所表示
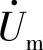 的称为最大值相量。
的称为最大值相量。
同理可得,正弦电流 i = I m sin( ωt + φ i )的相量是

正弦电动势 e = E m sin( ωt + φ e )的相量是

应该指出的是, 相量只是正弦电量的表示式,两者并不相等 。因为在正弦电量中包含幅值、角频率、初相位这三要素,而相量中没有角频率这个要素。正弦电量与表示它的相量之间有单一的对应关系,如

在了解相量表示法的引出思路后,当给出一个正弦电量后,就要能够写出它所对应的相量;同样的,当已知正弦电量的相量,并已知其角频率 ω ,就能够写出相对应的正弦电量的瞬时值表达式。
什么是相量图?相量在复数平面上的几何图形表示就是 相量图 。
假设有正弦电压,
u
=
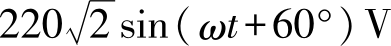 ,转换为相应的相量形式为
,转换为相应的相量形式为
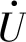 =220∠60°V;正弦电流
i
=
=220∠60°V;正弦电流
i
=
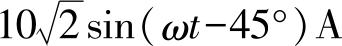 ,转换为相应的相量形式为
,转换为相应的相量形式为
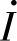 =10∠-45°A。电压相量和电流相量的模可按照各自确定的比率选取,相量图如图2-15所示。
=10∠-45°A。电压相量和电流相量的模可按照各自确定的比率选取,相量图如图2-15所示。
需要注意的是,在 同一个相量图中各相量所代表的正弦电量的频率必须是相同 的。因为只有这样,才能比较它们的相位关系。因此, 不同频率正弦电量的相量不能画在同一个相量图中 。
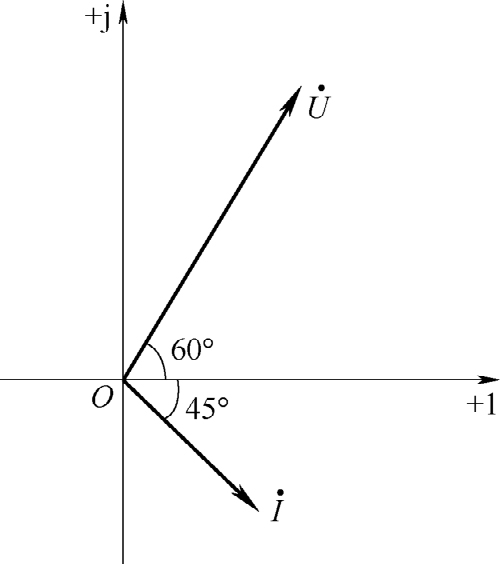
图2-15 相量图
相量计算法是分析计算交流电路的工具。多个同频率正弦电量进行加、减运算,其运算结果仍是同频率的正弦电量。例如, u = u 1 ± u 2 。根据复数运算法则,可以将前式变换成相应的相量形式

通过相量运算得到运算结果后,相量再经过反变换,就可以得到所求正弦电量的瞬时值表示式。
电能表又称 电度表、火表、千瓦小时表 。单相电能表是一种用于测量单相电能的装置,采用机械式或电子式测量原理。一般是民用,接220V的设备。计量单位是kW·h,即1kW负荷工作1h所消耗电能。其主要由电压线圈、电流线圈、转盘、转轴、制动磁铁、齿轮、计度器等组成。电能表是利用电压和电流线圈在铝盘上产生的涡流与交变磁通相互作用产生电磁力,使铝盘转动,同时引入制动力矩,使铝盘转速与负载功率成正比,通过轴向齿轮传动,由计度器计算出转盘转数而测定出电能。
单相电能表实物图和仿真软件中的电能表示意图如图2-16和图2-17所示。
家用单相电能表接线方法:四个接线柱,从左到右分别接相线进线、相线出线、零线进线、零线出线。例如,从左往右分别是端子1、2、3、4。端子1、2接相线,一般1进2出;端子3、4接零线,一般3进4出,如图2-18所示。

图2-16 单相机械式电能表实物图、仿真软件中单相机械式电能表示意图

图2-17 单相电子式电能表实物图、仿真软件中单相电子式电能表示意图

图2-18 单相电能表接线示意图
双控开关,也称 单刀双掷开关 (Single Pole Double Throw,SPDT)。图形符号如图2-19所示,有三个接线端,分别是L、L 1 、L 2 ,当将L、L 2 接入回路中时,若触头在L、L 2 之间,则回路接通;当触头在L、L 1 之间,则回路断开。家庭照明电路中使用的双控开关在仿真软件中的实物图(正反面)如图2-20所示。
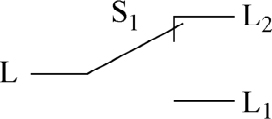
图2-19 双控开关图形符号
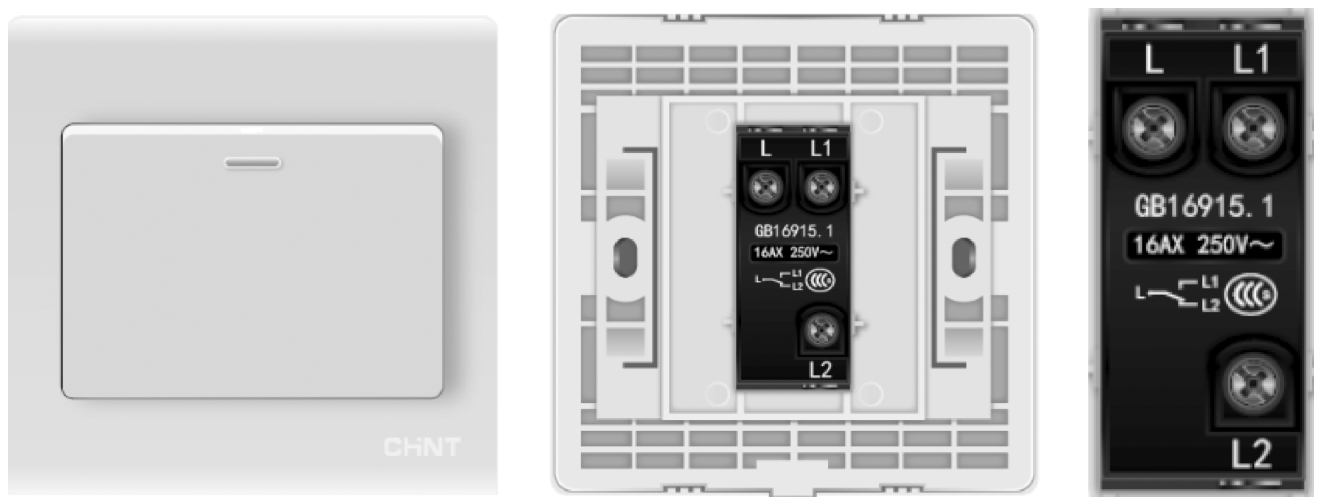
图2-20 双控开关实物图、反面示意图
1.正弦交流电量的三要素:__________、__________、__________。
2.工频交流电的频率是__________Hz。
3.周期、频率和角频率三者间满足的关系是__________。
4.已知 u =20sin(314 t +π/4)V,则 u 的幅值是__________,有效值是__________,角频率是__________,初相角是__________。
5.用电流表测得一正弦交流电路的电流为8A,则其最大值为__________。
1.已知正弦量 i =10sin(20π t +30°), u =220sin(20π t -120°),则电压 u 与电流 i 的相位关系是( )。
A.电压超前电流150°
B.电流超前电压150°
C.电压超前电流90°
D.电流超前电压90°
2.标有“220V/40W”的白炽灯,其中220V指的是所接电压的( )。
A.瞬时值
B.最大值
C.平均值
D.有效值
3.某正弦电压最大值为380V,频率为50Hz,计时始数值等于380V,其瞬时值表达式为( )。
A. u =380sin314 t V
B.
u
=
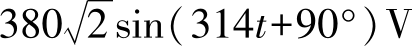
C. u =380sin(314 t +90°)V
D. u =380sin(314 t +45°)V