




在研究和评估各种无线通信技术时,都需要用到无线信道模型,它是描绘复杂无线信号传播的有效手段。因此,如何准确而高效地建立信道模型一直是研究的热点。下面介绍一些经典的信道建模方法和信道模型。
现有的信道建模方法主要分为统计性建模方法、确定性建模方法和半确定性建模方法,具体分类如图2-5所示。
(1)统计性建模方法主要依赖于信道测量,是基于无线信道的各种统计特性来建立信道模型的。
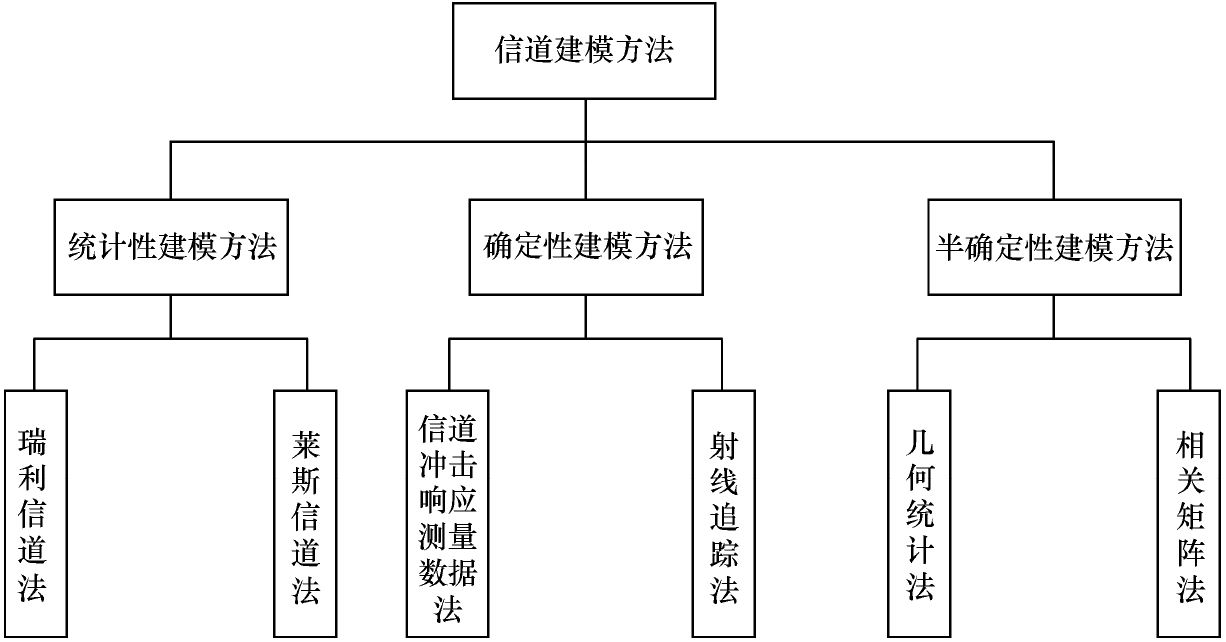
图2-5 信道建模方法分类
基于统计特性的建模方法需要给出AOD、AOA、PAS、AS等一系列参数。统计性建模方法能够较为全面地反映MIMO信道的衰落特性,特别是信道的空间衰落特性,这种方法的优点是建立的模型的复杂度较低,具有一定的通用性;缺点是和实际的信道有较大偏差。统计性建模方法分为瑞利信道法和莱斯信道法,基于统计特性建立的模型主要有李氏模型、离散均匀分布模型等。
(2)确定性建模方法利用传播环境的具体地理和形态信息,依据电磁波传播理论或者光学射线理论来分析并预测无线传播模型。该方法要求得到非常详细的信道环境信息,如地理特征、建筑结构、位置和材料特性等,环境描述的精度越高,模型越接近实际的传播情况。确定性建模方法分为信道冲击响应测量数据法和射线追踪法。
信道冲击响应测量数据法首先对实际通信信道的衰落进行测量,得到此通信环境下电磁波传播的信道冲击响应的测量数据,然后利用正弦波叠加的方法来模拟信道。
这一建模方法的优点是建模复杂度较低,过程也简单,而且很精确;但是该建模方法只能表示当前环境的通信场景,一旦通信环境改变,就需要重新进行测量,因此该建模方法适用于特定的传播环境。
射线追踪法在发射端通过多条传输射线来模拟实际的发射信号,射线在传输过程中会受到各种障碍物的阻碍作用,经历了发射、散射和衍射等多种传输机制,最终到达接收点。通过这种方法,能够计算出信号的幅度、相位、到达角及传输时延等有效信息,进而可以构建出信道矩阵 H 。
这一建模方法的优点是能够获得较为准确的传播预测,但是计算时间较长,而且对仿真的内存需求也很大。
(3)半确定性建模方法基于确定性建模方法用于一般的市区或室内环境中导出的公式,为改善公式的精度,使其保持和实验结果的一致性,需要根据实验结果对公式进行适当的修正。我们通常使用半确定性建模方法来仿真。
半确定性建模方法建立的模型是综合上述两种模型的优点发展起来的一种低复杂性,又能较好地符合实际环境的一种信道模型。这种模型的实现方法主要有两种,即几何统计法和相关矩阵法。
几何统计法是对确定性建模方法中的射线追踪法的一种简化,它不需要详细地知道信道环境,也不需要对特定的环境生成电子地图。它根据一定的统计特性,在基站和移动台周围随机散布散射体组,对于每一个散射体组中的散射体要符合测量统计出来的特定角度时延功率谱。每个散射体组对应信道模型中的一条路径,而每组中散射体反射、散射和绕射到接收端的射线就组成路径中的各条子路径。用射线追踪法来确定每条射线的角度、时延等信道参数。在接收端将这些射线叠加起来就得到了信道冲激响应。
几何统计法的优点是不依赖于传播环境中散射体的分布情况,只要改变信道的传输参数,就可以进行场景的切换。
相关矩阵法是根据基站端和用户端的相关矩阵,通过笛卡儿卷积得到各传输链路间的系数。其优点是模型简单,计算量小。
单天线的信道模型一般比较简单,如最简单的加性高斯白噪声(AWGN)信道,该信道只有高斯白噪声,或者Jakes模型等。但随着MIMO技术的研究与应用的发展,MIMO的信道模型也被开发出来,并不断发展。
早期的MIMO信道模型研究为简化分析,通常假设天线阵列周围存在大量的散射物,并且天线间距大于半个波长,不同天线的信道衰落是不相关的。在仿真中通常利用3GPP中的典型城市信道来模拟MIMO信道,各个天线的信道是独立产生的,相互之间独立,即相关系数为零。随着MIMO信道的研究发展逐渐趋于成熟,我们发现随着MIMO信道相关性的逐渐增强,MIMO信道的容量将急剧下降。而现实环境中,具有相关性或相关性强的MIMO信道环境又大量存在,所以要在MIMO信道研究中考虑建立接近实际信道环境的MIMO信道模型。除了天线相关性,还要考虑极化天线建模。
下面简要介绍在3G及B3G/4G/NR系统中采用的MIMO信道模型 [6-11] ,其中,包括空间信道模型(SCM) [6] 、SCM扩展模型(SCME) [7] 、IMT-Advanced信道模型 [8] 、WINNER信道模型 [9] ,IEEE802.16m系统评估模型(EVM) [10] 、3D MIMO信道模型 [11] 、NR MIMO信道模型 [12] 。
3GPP在TR 25.996中提出的SCM起初是为载频为2GHz、带宽为5MHz的系统设计的,但由于在IMT-Advanced系统的带宽扩大到20~100MHz,所需要的采样频率也大大提高,每条链路能分辨的时延数量也随之增大,仅包括6条时延路径的SCM不再满足系统的需要,因此SCME顺势而生。
然而,为保持模型的一致性和可比性,SCME的设计考虑了与SCM的后向兼容,这限制了SCME的性能,这也是后续逐渐开始使用新的WINNER信道模型的原因。WINNER信道模型的参数是从目标信道探测测量中提取的,并且利用信道统计特性,在终端和基站周围撒满散射体组来模拟实际电磁波的反射、折射等,从而实现对实际信道的模拟。Rel-13中FD MIMO的引入,进一步在现有的MIMO信道中引入了垂直角度EOA和EOD,从而形成了3D信道模型。而在NR中,由于高频的应用,3D信道模型进一步改进,形成了NR MIMO信道模型。这些信道模型(除了802.16m的信道相关矩阵法建模)都是将信道分成多个簇(Cluster),每个簇对应不同的时延、功率、离开角和到达角。而每个簇中包括多个不同方向的射线(Ray),对于最弱的 L 1个簇,每个射线有相同的时延和功率,以及不同的离开角和到达角。射线的离开角和到达角基于所在簇的离开角或到达角加一个角度偏置生成。而对于最强的 L 2个簇(一般 L 2=2),会进一步分成多个子簇,每个子簇的功率和时延相同,而子簇间的功率、时延不同。
本节将对经典的MIMO信道模型进行简要介绍,2.4节将详细介绍用于5G NR技术标准研发的5G NR信道模型。
需要说明的是,在不同的信道模型中,由于参与组织的不同,所用的一些名称可能不同,但它们表达的是相似或者相近的概念。比如簇(Cluster)在有的模型中表示为径(Path)、射线(Ray),在有的模型中表示为子径(Sub-path),子簇对应中径。
3GPP TR 25.996 [6] 协议定义了SCM。SCM是为载频为2GHz、带宽5MHz的系统设计的。SCM原本专用于室外传播,定义了3种环境,即市区宏小区(又称城市宏,UMa)、郊区宏小区(SMa)和市区微小区(又称城市微,UMi),其中,只有UMi场景考虑了LOS条件。关于路损模型,SCM采用的是经过适当调整的COST 231 Urban Hata与COST 231 Walfish-Ikegami模型,它们分别被用于1.9GHz频段的宏小区和微小区,但模型在其他频率范围的适用性没有进一步地分析。另外,在SCM中,对于从一个终端到不同的BS链路的阴影衰落标准差具有恒定的相关系数(0.5)。
SCME [7] 由SCM演变而来。SCM主要应用于载波频段为2GHz、带宽为5MHz的CDMA系统,SCME主要应用于载波频段为2GHz和5GHz、带宽为5MHz以上(包括100MHz)的通信系统。
SCM不支持宏小区场景下基于视线(LOS)路径,SCME没有扩展仿真场景,但提供了对宏小区场景下LOS路径的支持,另外,SCME将20条子径进行分组,引入中径的概念,一条中径包含多条子径,以支持大带宽。
关于路损模型,SCME对与频率有关的自由空间损耗进行了修正,扩展了SCM场景的频率范围。
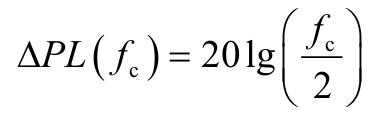
其中, f c 是载波频率,单位为GHz。另外,在SCME中,COST 231 Walfish-Ikegami路损模型(在SCM中原本用于微小区)也应用于5GHz范围的宏小区环境,因为更高频率的使用降低了覆盖。
IMT-Advanced定位于B3G通信系统,为了评估IMT-Advanced的系统性能,国际电信联盟(ITU)在ITU-R M.2135 [8] 中给出了相应的评估方法及信道模型,该模型也被3GPP TR 36.814所借鉴和采纳。
ITU信道模型包括以下两类。
① 采用数学统计的通用(Generic)模型,用于评估各种无线接入技术。
② 采用固定某些参数的簇时延线(CDL)模型,CDL模型可认为是抽头时延线(TDL)模型的空间扩展。TDL模型定义多径抽头的功率、时延、多普勒频谱信息;CDL模型定义了多径的功率、时延、角度、用户移动速度信息。
ITU信道模型的簇概念相当于多条子径所组成的路径,簇内的射线相当于子径。另外,ITU通用(Generic)信道模型包括基本模型(Primary Model)及扩展模型(Extended Model),基本模型的框架基于WINNER2(WINNER PhaseⅡ)信道模型,该模型的建模方法与3GPP/3GPP2的SCM基本相同。
通过从测量的信道脉冲响应中获得的时间和空间参数,WINNER信道模型 [9] 能够刻画不同的环境或场景。每一种场景都会分析和处理测量数据,以获得指定场景的参数。随后,同样的通用信道用于建模所有的场景,只是使用了不同的控制参数值。与SCM/SCME相比,WINNER信道模型支持更多的场景。其中,WINNER1信道模型定义了以下场景:A1-室内(办公室/住宅)、B1-典型市区微小区、B3-室内热点、B5-包括具有不同部署设想的子场景(a、b、d)的都市热点(终端移动速度为零)、C1-郊区、C2-典型市区宏小区、D1-农村宏小区。WINNER2信道模型又进一步扩展了上述覆盖场景:A2-室内到室外、B4-室外到室内、B5-包括具有不同部署设想的子场景(c、f)的都市热点(终端移动速度为零)、D2a-移动网络、B2-恶劣市区微小区、C3-恶劣市区宏小区。通常,甚至对于同样的场景,LOS组件的存在也会大幅影响模型参数的值。关于这一属性,每个WINNER场景在LOS与NLOS条件方面是有区别的。根据SCME的方法,WINNER信道模型定义的所有场景都支持依赖于频率的路损模型,且对于2~6GHz的频率范围都是有效的。WINNER路损模型主要基于在5.2GHz频率范围内进行测量。
测量系统支持100MHz带宽,在WINNER信道模型参数化期间,簇(Cluster)的数量与时延和角度域有关。因此,簇的数量能够反映系统带宽和场景。另外,与SCM/SCME相比,WINNER信道模型支持连接到同一BS的不同终端间的LOS概率的相关性。
显然,与其他模型相比,WINNER信道模型的种类更多,适用的场景更为细化,对通信系统的性能评估更为精确。WINNER信道模型的建模方式与ITU信道模型较为接近,但信道参数有所不同,因篇幅所限,本节不再详细论述。
802.16m标准制定的性能评估方法文档中的空间信道模型同时支持射线追踪法和相关矩阵法 [10] ,其中,相关矩阵法是首选方法。
由于相关矩阵法在很多步骤上与射线追踪法相同,所以在此以SCM为基础,主要描述相关矩阵法的特殊之处。下面介绍相关矩阵的计算过程。
(1)每径相关函数
根据基站/终端天线的角度扩展
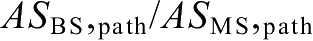 、基站/终端天线配置(主瓣方向、天线间距、天线数量、极化特性)等计算每径的空间相关矩阵。
、基站/终端天线配置(主瓣方向、天线间距、天线数量、极化特性)等计算每径的空间相关矩阵。
说明:只要每径AS、mean AOA和mean AOD确定了,理论上基站侧、终端侧天线空间相关性就确定了。假设每径AS为拉普拉斯(Laplacian)功率角分布,天线为全向天线,则基站(或终端)的第 p 根和第 q 根天线间的空间相关性为
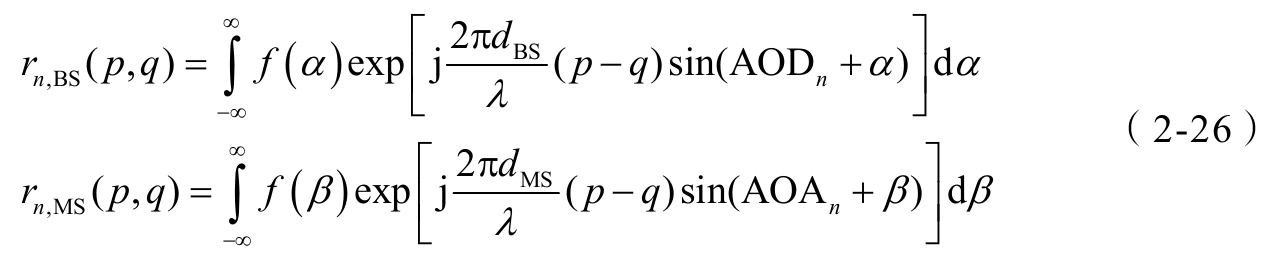
d BS ( d MS )为基站(终端)天线间距, λ 为波长。 α 为围绕基站侧平均AOD的偏差, β 为围绕终端侧平均AOA的偏差,其概率密度函数为
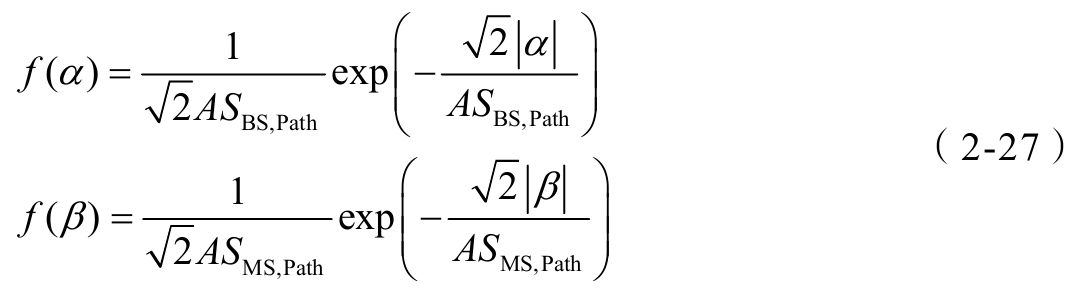
(2)每径相关函数求解(近似)
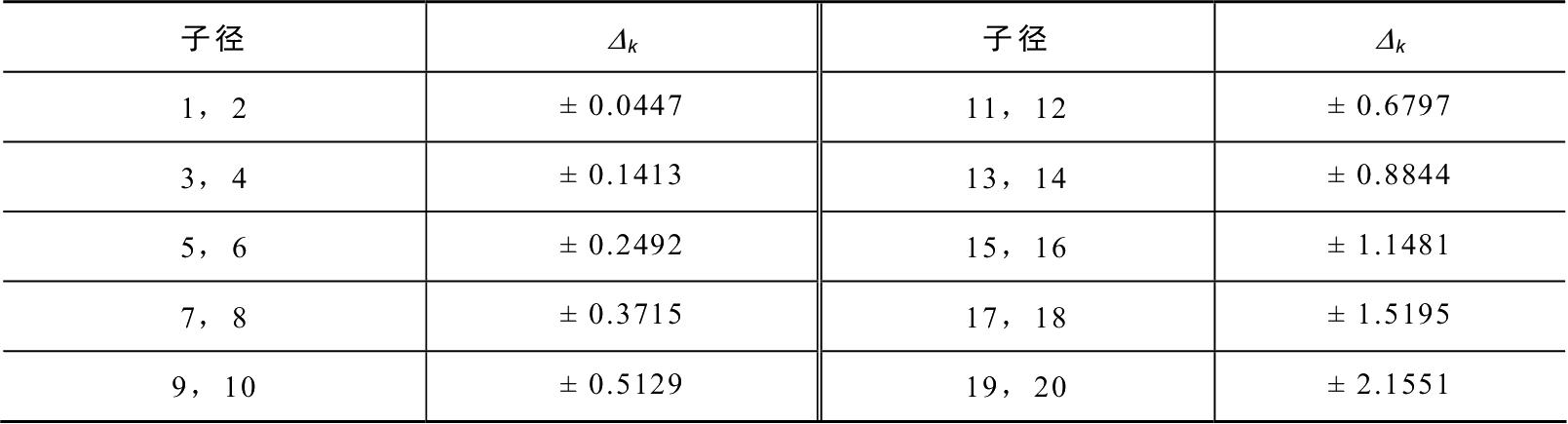
使用20个子径来逼近Laplacian分布,每路径用20个子径逼近,每个子径的相对于每路径角度均值的角度偏移如表2-1所示。
表2-1 子径角度偏移
基站(或终端)的第 p 根和第 q 根天线间的线性阵列下空间相关性为
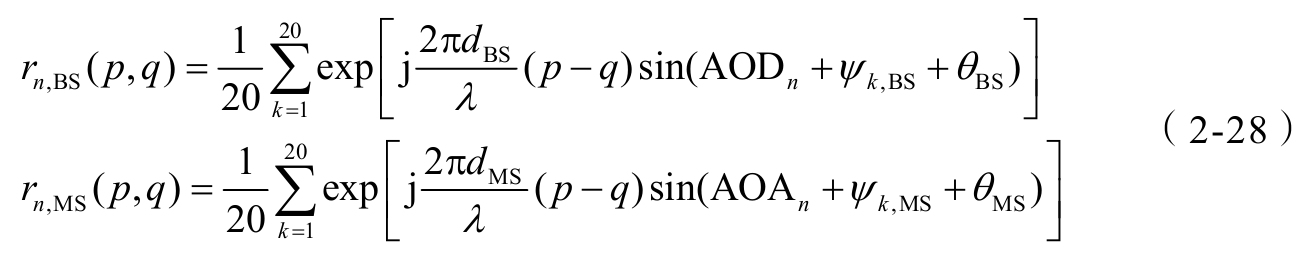
(3)每径(per-tap)的空间相关矩阵
每径的空间相关矩阵为

基站侧tap
n
的空间相关矩阵为
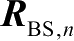 ,终端侧tap
n
的空间相关矩阵为
,终端侧tap
n
的空间相关矩阵为
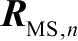 。
。
如果天线(接收 N 根,发射 M 根)为交叉极化天线,则每径的空间相关矩阵为
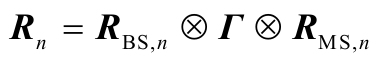
当所有接收天线为同一极化方向,
 为
N
×
N
矩阵;当所有接收天线为交叉极化时,
为
N
×
N
矩阵;当所有接收天线为交叉极化时,
 为(
N
/2)×(
N
/2)矩阵。
为(
N
/2)×(
N
/2)矩阵。
在长期演进的Rel-13以前,MIMO的主要研究都集中在开发空域的水平维度。为了进一步开发MIMO技术的性能,需要对空域的垂直维度进行开发。因此,随着MIMO研究的深入,有必要将垂直维度的空间特性引入无线通信系统。Rel-13在SCME的信道的基础上,引入垂直维度,这就是3D MIMO信道。3D MIMO信道 [11] 的建模参数主要有:时延扩展DS、水平离开角(方位角,Azimuth)AOD的角度扩展、水平到达角(AOA)的角度扩展、垂直离开角(俯仰角,Elevation)EOD的角度扩展、垂直到达角(EOA)的角度扩展、阴影衰落(SF)的标准差、莱斯因子(K)。需要说明的是,在已有的模型中,比如NR MIMO [12] ,垂直离开角(顶点角,Zenith)为ZOD,而垂直到达角为ZOA。它们的关系是ZOD/ZOA以 z 轴的正方向为0°,而EOD/EOA以水平方向为0°,即EOD/EOA的值是对应的ZOD/ZOA的值减去90°。
3D MIMO信道模型对高频不是很适用,而高频是NR中提高系统传输效率的有效手段,所以NR MIMO信道 [12] 在3D MIMO信道的基础上进一步演进,支持载频范围为0.5~100GHz,并引入很多新的特性,如空间一致性、阻挡、氧吸等,这些将会在2.4.8节重点介绍。
NR MIMO信道模型主要包括:城市微(UMi)、城市宏(UMa)、乡村宏(RMa)及室内(Indoor)环境等。
信道模型有很多,这里主要以TR 38.901-v16.0.0为基础进行介绍,以便了解信道建模的过程和原理。其中,2.4.1~2.4.7节是信道模型的基础部分;2.4.8节是信道模型的扩展部分,是进行深入研究和一些特殊场景仿真需要了解的部分,例如高频中验证空间一致性、旋转、阻挡等特性,或者大带宽、大阵列的场景,双反射场景。为了加强对信道建模的了解,使模型更符合实际信道,增加了2.4.9节(混合建模的相关内容),读者可以根据需要了解2.4.8节和2.4.9节的内容。