下载掌阅APP，畅读海量书库
立即打开
脉冲信号序列即为无线信道的冲击响应，表示为
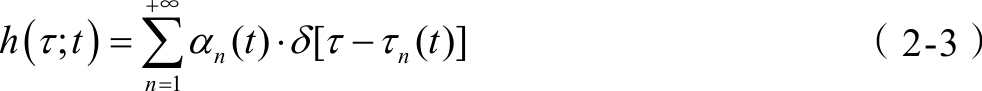
在理论建模和实际接收机处理中，多径数量是有限的，即
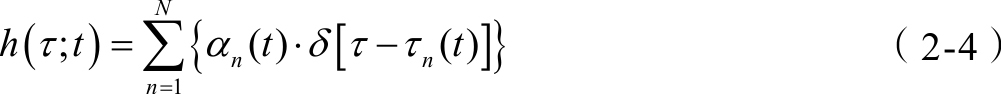
其中， α n （ t ）表示第 n 径接收信号的衰减因子，为实数（只有幅度衰减）或复数（幅度衰减和相位偏转）； τ n （ t ）表示第 n 径的传播时延。
在发射端，天线上发送的射频信号 s （ t ）表示为
单载波系统中， s l （ t ）为信道编码后的已调制符号，例如正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）系统，为时域的OFDM符号，一般为复数，常被称作射频信号 s （ t ）的复包络或等效（复）低通信号。
在接收端，实际接收信号则为 s （ t ）与 h （ τ ; t ）的线性卷积，即
进一步地，如果 α n （ t ）是实数，则
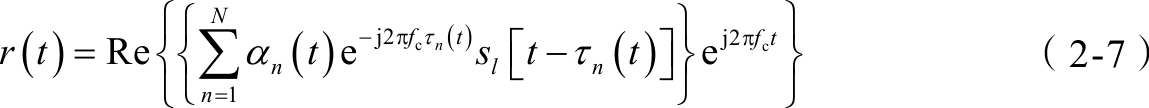
如果 α n （ t ）是复数，则
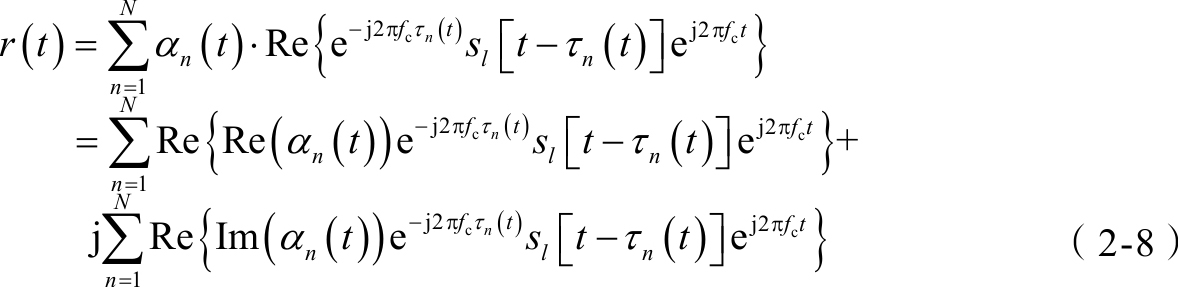
等效基带（或低通）接收信号则为
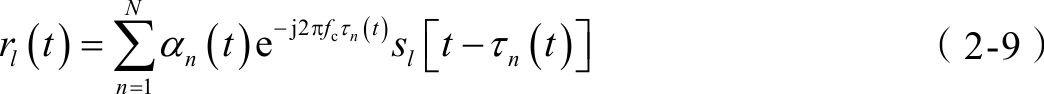
r l （ t ）是以等效低通信号 s l （ t ）为输入时的等效低通输出信号，此时，等效低通信道响应为
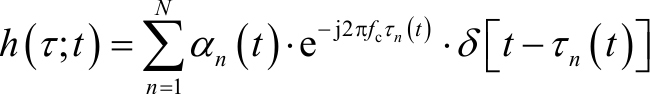
考虑多普勒频移时，每径的频移为 f n ，则等效低通信道响应变为
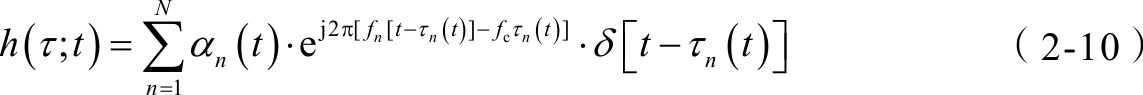
信道建模使用一些随机变量或过程逼近 h （ τ ; t ）。单天线时， h （ τ ; t ）为一个时变的标量，多天线时， h （ τ ; t ）为一个时变向量或矩阵。
通常来说， h （ τ ; t ）的统计特性满足瑞利分布或者莱斯分布。
在无线通信信道环境中，电磁波经过反射、折射、散射等多条路径传播到达接收机后，总信号的幅度服从瑞利分布，也称信号幅度服从瑞利衰落。瑞利分布是一个均值为0，方差为 σ 2 的平稳窄带高斯过程，其概率密度公式为
为了说明多径信道下的信道服从瑞利衰落，在此先解释广义平稳窄带过程的定义。
任意随机过程经过高频信号调制后就变为窄带随机过程，如果该随机过程是广义平稳的，则该窄带随机过程就称为广义平稳窄带过程；如果该随机过程是高斯的，则该广义平稳窄带随机过程就称为广义平稳窄带高斯过程。
原始信号是个随机过程，为了长距离的无线通信，原始信号都要经过载频（均为高频信号）调制，所以，发射后的信号都是窄带信号。而无线传播环境内存在大量的障碍物和散射体，则调制信号到达接收机时，已变为大量不同时延、不同衰减的调制信号副本信号的叠加，而且副本间统计独立。根据中心极限定理，大量独立随机变量之和的分布趋近于高斯分布，即可认为接收信号为高斯过程。所以，接收的信号是一个窄带高斯过程，至于是否平稳，严格来讲则要基于研究的需要。下面将证明信道服从瑞利衰落。
考虑多径和多普勒时，接收信号为
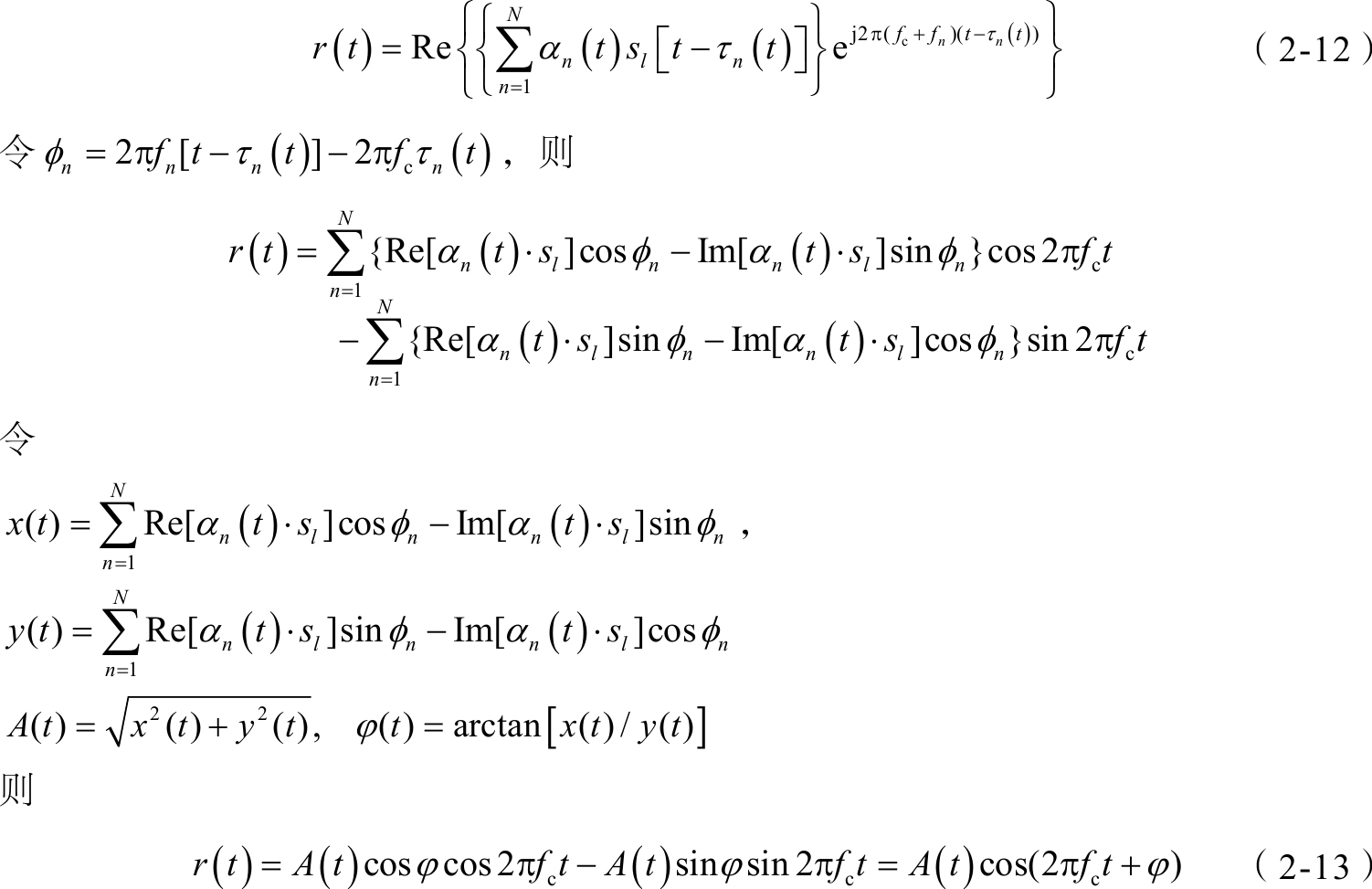
为了计算 A （ t ）和 φ ( t )的概率分布，需要考察 x ( t )和 y ( t )的独立性问题。请注意，根据之前的分析，计算必须基于 r ( t )是平稳窄带零均值高斯随机过程这一条件。
根据公式（2-13）、 x （ t ）= A （ t ）cos φ 和 y ( t )= A （ t ）sin φ ， r （ t ）的期望为
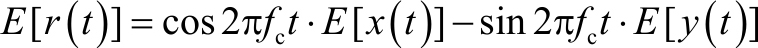
因为 r （ t ）平稳，即对任何 E [ r （ t ）]=0，则 E [ x （ t ）]= E [ y （ t ）]=0。
r （ t ）的自相关函数为
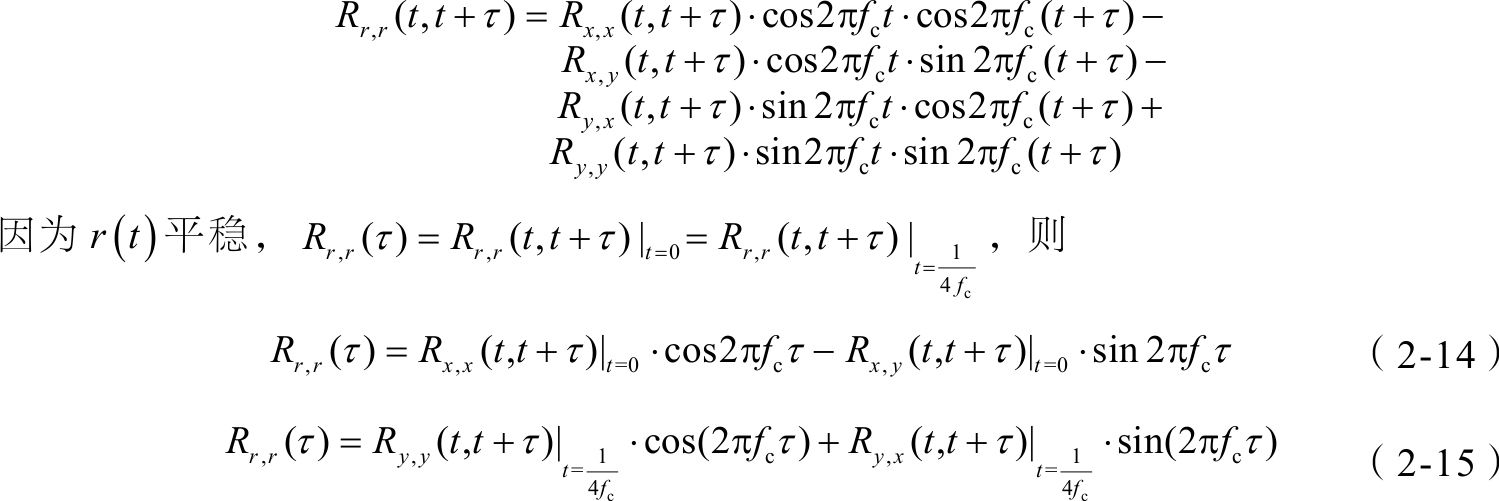
为了保证 r （ t ）平稳，必须要求 x （ t ）和 y （ t ）分别且互相关平稳，并满足
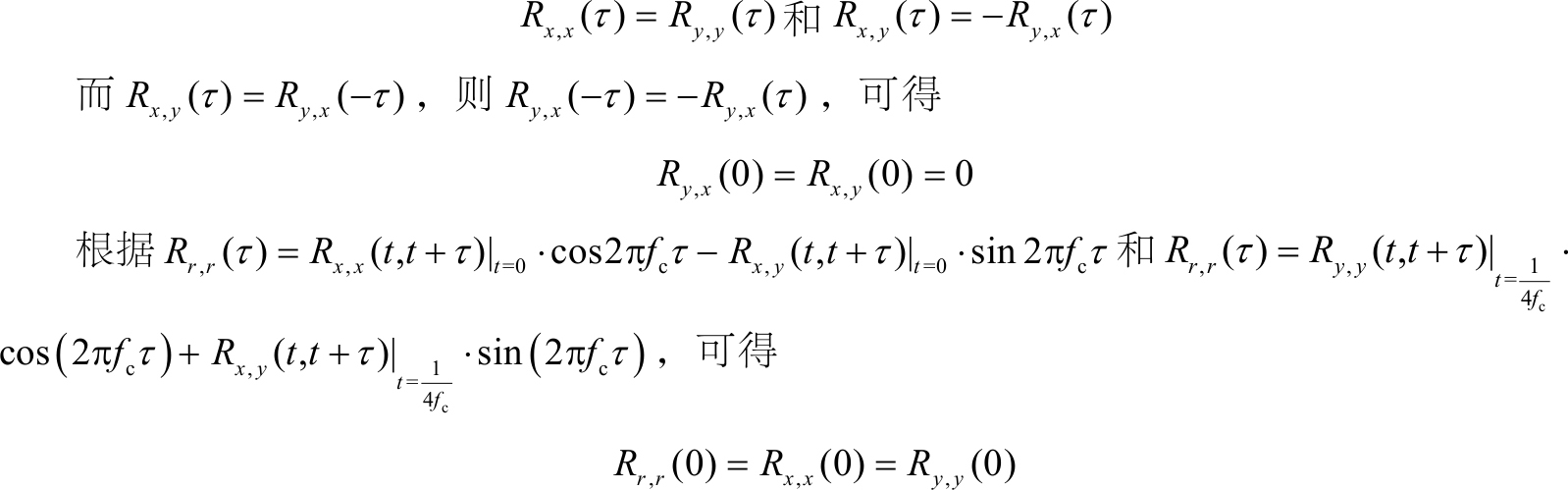
另外，根据
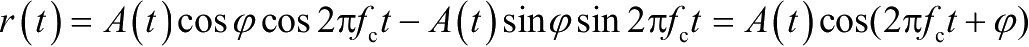，可得
r
(0)=
x
(0)、
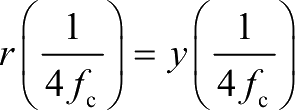。由于
x
(
t
)和
y
(
t
)平稳，且
r
(
t
)服从高斯分布，则
x
(
t
)和
y
(
t
)亦服从高斯分布。
进一步地， x ( t )和 y ( t )的联合概率密度函数为
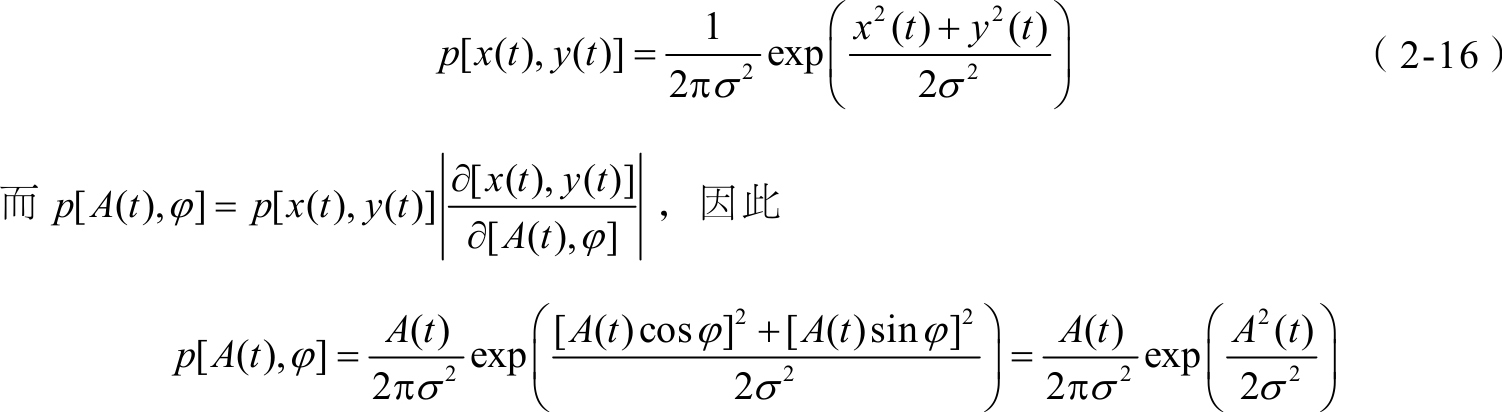
A ( t )和 φ ( t )的概率密度函数为
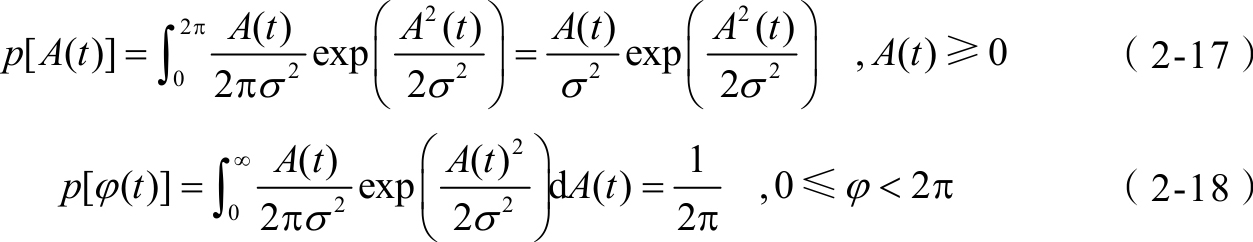
综上，接收信号的幅值服从瑞利分布，相位服从均匀分布。
根据 A ( t )的概率密度函数，可以计算得到：
● 接收信号幅度
A
(
t
)的均值为
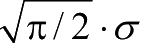，方差为
；
● 接收信号幅度 A ( t )最大取值为 σ 。
在接收信号中，除了2.2.2节提到的接收信号，还存在一个特殊的直射传播路径上的信号，在考虑多径效应和多普勒效应的情况下，接收信号为
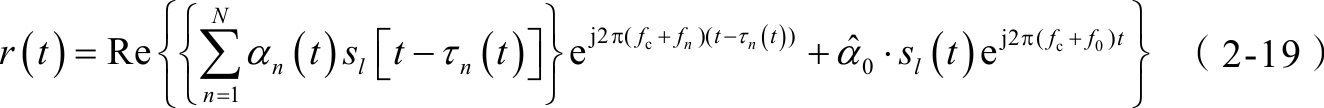
进一步地，假设 s l （ t ）为单位模值，相位为 θ ，则
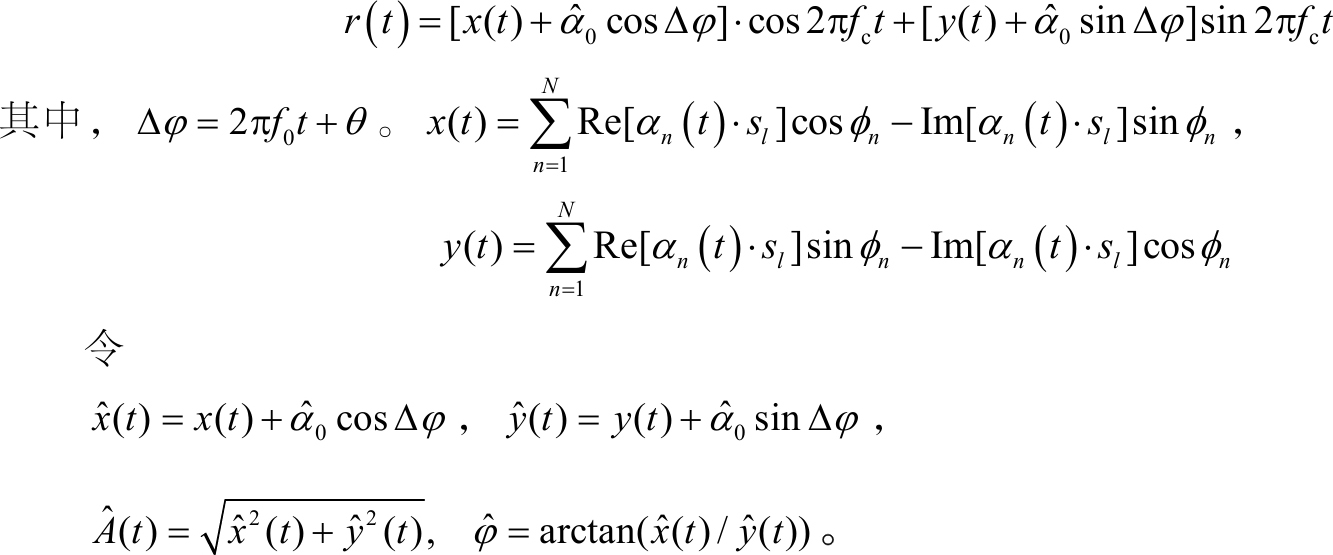
根据前文分析，
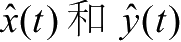将服从高斯分布，且独立。则在Δ
φ
确定的条件下，
和
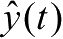的联合概率密度函数为
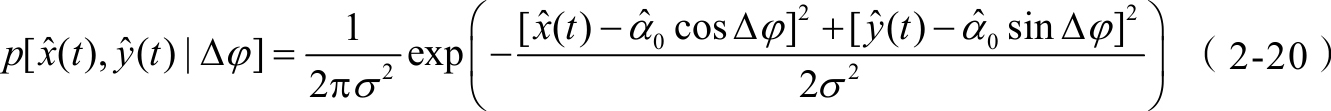
在Δ
φ
确定的条件下，
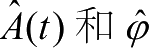的联合概率密度函数为
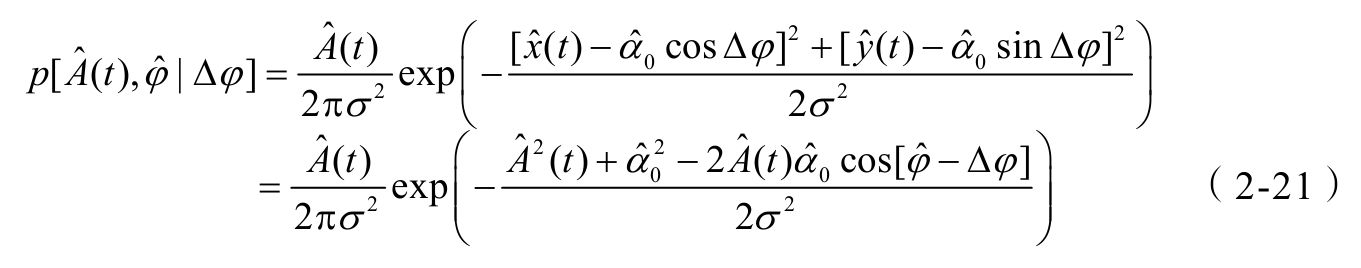
在Δ
φ
确定的条件下，
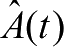的联合概率密度函数为
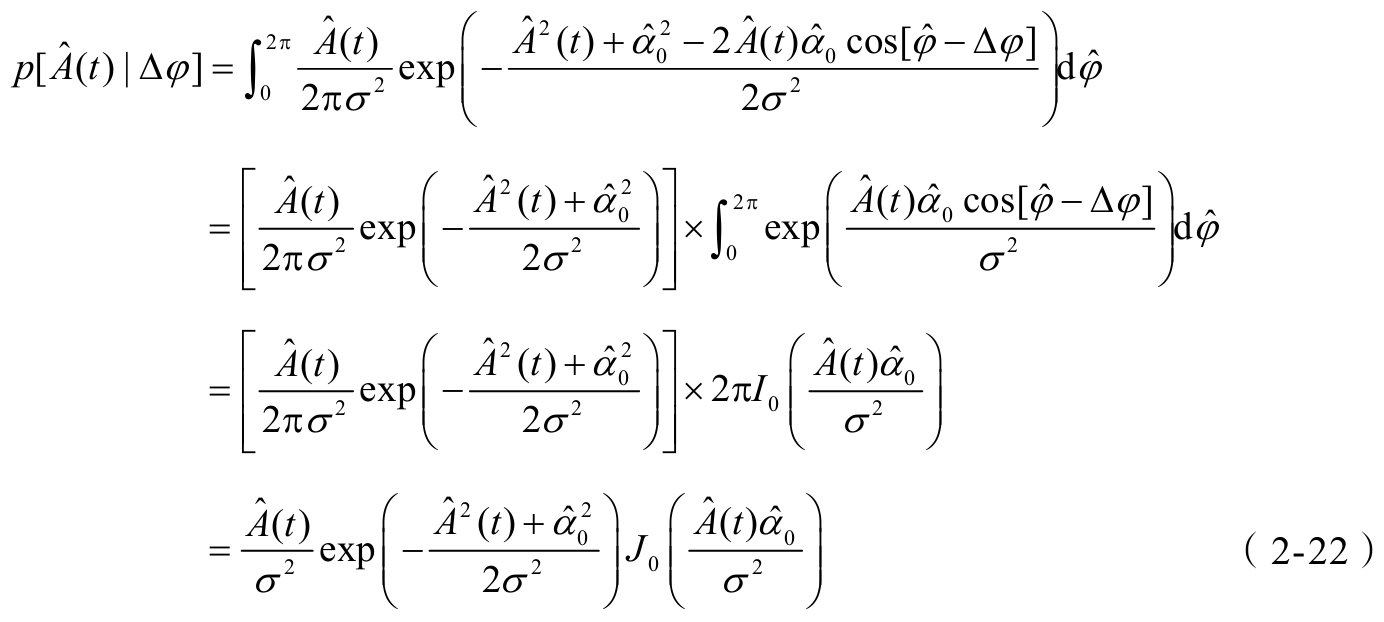
这里，
J
0
为修正的零阶贝塞尔函数。定义
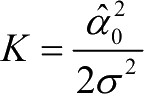为莱斯因子，表示LOS径相对于其他径的功率比。
发送端和接收端的相对移动使接收端的接收信号发生了频率偏移。当存在多个入射波时，频谱发生扩展，产生多普勒频谱。下面以U型谱（Jakes谱）为例，介绍多普勒频谱。
U型谱基于以下几个重要假设：
● 入射波足够多；
● 入射波到达角在（-
π
,
π
]内呈均匀分布：
；
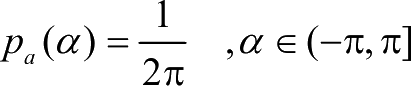● 接收天线具有各向同性的增益。
多普勒频移与到达角度 α 的关系： f = f max cos α ， f max 为最大多普勒频移。根据 α 的概率密度函数[这里仅取开区间（- π ,0）和（0, π ）]，且每个多普勒频移都对应两个可能的角度，可以求得 f 的概率密度函数为
又因为接收天线具有各向同性的增益，且到达角均匀分布，所以
S
(
f
)与
p
(
f
)成正比，且
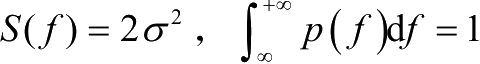，可得到功率谱密度为
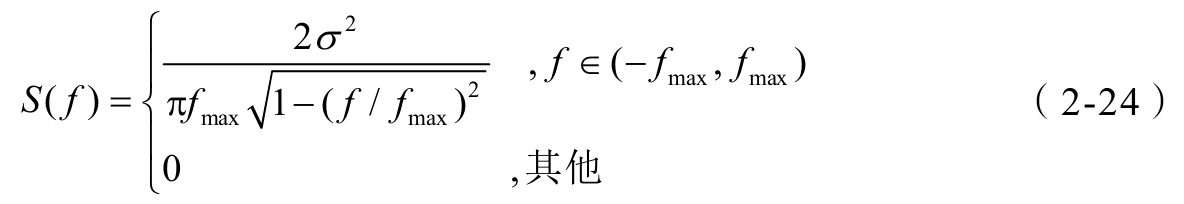
公式（2-24）为多普勒U形谱（Jakes频谱）， σ 为瑞利衰落的同相分量和正交分量的标准差。由于信道功率谱与信道相关函数是傅里叶变换对的关系，信道自相关函数为
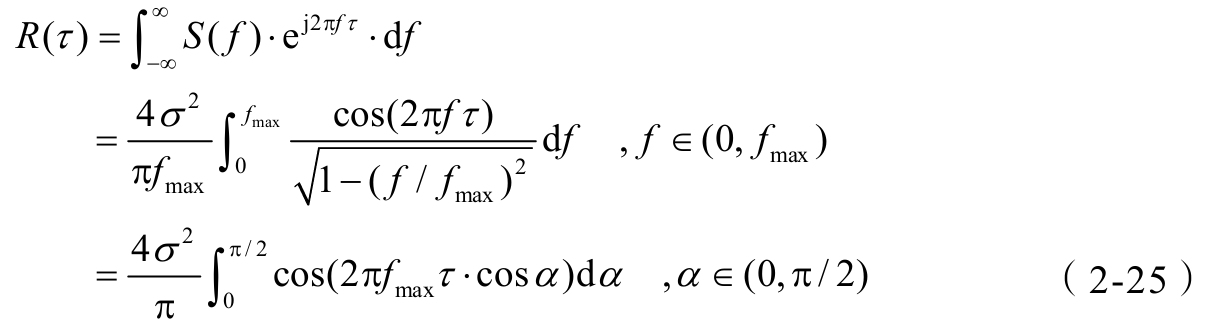
根据零阶贝塞尔函数定义
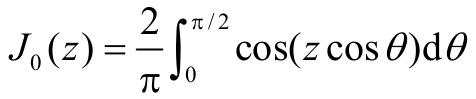
自相关函数为
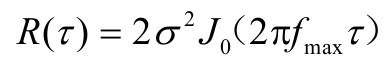
利用多普勒的频谱信息和自相关函数信息可以估计接收端的最大多普勒频移及其移动速度，它们对于通信系统的切换、负载均衡、未来通信系统的接入选择等而言，均是重要参数。