下载掌阅APP，畅读海量书库
立即打开
芒福德现为哈佛大学与布朗大学荣誉退休教授，研究领域是代数几何、图形视觉和模式理论。曾获菲尔兹奖（1974年）、麦克阿瑟奖（1987年）、邵逸夫奖（2006年）与沃尔夫奖（2008年）。
关于直角三角形三条边长度的法则（一般被称为毕氏定理，即毕达哥拉斯定理），现存最早的文献是公元前1800年左右汉穆拉比时代的古巴比伦泥板。我采纳霍伊鲁普（Jens Høyrup，1943—）的建议，称之为法则（rule），而非定理，因为在早期的大部分历史中，它是作为表达这些边长关系的规则，而不是定理出现的。更何况，我们根本不知道毕达哥拉斯是否证明了它。继巴比伦人之后，它又出现在现存的印度吠陀祭坛建造手册里，这些文献早在公元前800年完成，经由口述流传下来。由于中国秦朝烧失大量文献，我们能找到的最早记录只能上溯至公元前2世纪。这些线索的确稀少。但因为毕氏法则可以说是人类发现的第一个“非平凡”（non-trivial）的数学定理，所以关于它究竟是在何时何地最早出现的、它是不是各个文明独立发现的，以及它是如何被发现的，一直存在广泛的争论。这一切都属于韦伊所谓的“原史”（protohistory），即当某一传统的传世文献稀少，且可能不具有代表性，有些文明甚至付之阙如时，仍试图进行学术探索。毕氏法则即为原史的一个范例，它的完整历史为何，我们只能推测，而这正是我想在本文中讨论的。然而，我并非全是推测。我的推测大大得益于数学史家的深入研究，其中要特别感谢霍伊鲁普的大力协助。
我们该如何看待这类推测呢？我的观点是：历史永远是贝叶斯推断（Bayesian inference）的演练，不仅是原史，整个历史都是如此。我们永远不可能完全了解过去的时空。即使在我们自己的时空，我们也依赖于错误的和选择性的记忆来重构事件。学者经常会有一种错觉，以为若只依赖第一手资料，他们不会做出重大推论，但我认为他们错了。第一手资料当然远远胜过第二手资料，但每个人都会建立他们自己对人类行为与人类文化的个人先验（prior），借此把残存的稀少资料扩展为对某些事件的完整重构。的确，正如鲁西迪（Salman Rushdie，1947—）引述他的剑桥大学教授希伯特（Arthur Hibbert，1924—2008）的话：“在听到人们说话之前，你绝不要动笔写史。”当然，这也是后来几个世纪不同时期对同一事件的历史记载差异如此之大的根本原因。
我初次读阿基米德的个人经验足以阐明我的偏见：在适应了他的特殊用语以及当时数学文化的特质之后，我很确定我完全能跟上他的思路。我知道现在的数学家如何推理，而阿基米德研究数学的方式与我的自身经验非常吻合。我是在根据经验重构一幅丰富的阿基米德画像。他是在计算积分的黎曼和，是在做一些恼人的估计来建立收敛。我知道历史学家会说，我读到的并不是他真正的意思，而是用我对数学的现代理解来扭曲他的话。这一点我无法反驳，但我不同意。我把数学看成一个问题与解答的固定集合，它独立于文化，就像冶金学是能用于分析古代刀剑的一组事实的固定集合。与之类似，当我在阿基米德的著作中读到如同现代人所写的数学（调整过符号记法之后）时，我自认能听到他“说话”。
回到毕氏法则。我想该问的第一个问题是：为何古人要研究三角形？我认为，有两个相关且非常有说服力的原因。一个原因是土地的价值依其面积而定，若要买卖、继承和课税，面积的数值是必不可少的；另一个原因是当城镇发展成都市时，建筑物和街道规划最便利的形状是矩形。对于第一种情形，最自然的方法是把田地分割成近似的矩形或直角三角形。直角三角形是矩形的一半，一个矩形可以通过对角线分成两个直角三角形。所以你要能在地上画出垂直线，要能辨认一个四边形是否为矩形，也要能分辨出三角形的一个角是否为直角。换句话说，所有古代王国的统治者都需要熟练的土地测量员和精通几何学的建筑大师。这并不表示他们必须懂得毕氏法则，但它暗示了毕氏法则是很有用的。
在美索不达米亚，非常幸运的是，由于文书是记在湿泥板上，而不是写在纸张、莎草纸、树皮或绳子上的，因此几乎可以永久保存。例如，火焚不会毁坏泥板，反而会让它更持久。在美索不达米亚，我们有将近三千年的泥板或泥块记录，从中可以重建其文化史。施曼特-贝瑟拉（Denise Schmandt-Besserat，1933—）运用这些资料构建了一个非常有说服力的关于公元前3000年美索不达米亚的文字起源的故事：人们一开始用泥块记录，然后有了泥封（clay envelope），最后是写在泥板上的楔形文字。从本质上讲，她的理论认为，一切都是从记下“某某人欠了什么什么”开始的。他们高度复杂的六十进制算术似乎源于要有一套统一的中央会计制度（可能在乌尔第三王朝），包括用各种单位来衡量的商品和劳动，常写成4、5、6、10、12等的倍数。现存有许多独特的会计泥板，上面详细记载了劳动和物品，可参考马特西奇（Richard Mattessich）的著作《会计与会计思想的起源》（ The Beginnings of Accounting and Accounting Thought ）。
那么，土地测量呢？据说女神尼萨巴（Nisaba）从恩利尔（Enlil）那里得到识字和计算能力作为结婚礼物，又将之传递给人类。下面这首歌颂她的美妙赞歌出自古巴比伦时期的一块泥板：
尼萨巴，绽放喜悦的女神。
正直的女神、书吏，知晓一切之神：
她引导你的手指在黏土上书写，
让你的手指在泥板上刻上美丽的楔形，
让楔形因黄金尖笔而绽放，
芦苇测杆与青金石准绳，
标杆以及赋予智慧的书写板：
尼萨巴慷慨地把它们赐予你。
图1 史柯恩珍藏MS 3049的古巴比伦泥板：毕氏法则于公元前1700年被使用
“芦苇测杆”和“准绳”是测量员的基本工具，在此被放在与文字同等重要的地位。许多流传下来的“地契”泥板附有平面图和长度。但在我看来，最能充分展现他们关于毕氏法则知识的，是史柯恩珍藏（Schøyen Collection）MS 3049的古巴比伦泥板（见图1）。这块泥板的作者在此计算一道厚重城墙的门道从左下角到右上角的距离。现在一般是把毕氏法则视为关于三角形的定理，但它描述的其实是二维笛卡儿坐标下的距离。迭代下去，我们可以得到
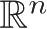中的距离是每一坐标改变值的平方和开根号：
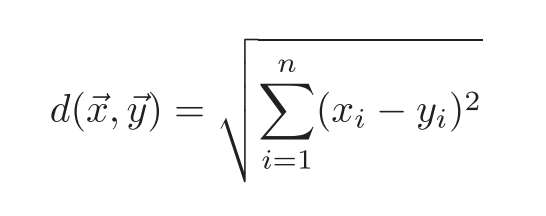
毕氏法则的重要性在于这个推论。而我们发现，早在公元前17世纪，在古巴比伦的乌鲁克，人们已将之用于三维空间。
若一人要求城门内部对角线长，
5肘，为25，又10指，为1 40
此乃城门高。
xxxxx 表格，
于此输入20及 xxxx ，
你得到26 40，城门宽是8 53 20，
城墙厚是6 40。
城墙高26 40，使自噬，则
你得到11 51 06 40。
城门宽8 53 20，使自噬，则
你得到1 19……44 26 40。
城墙厚6 40，使自噬，则
你得到……44 26 40。
叠上三数，你得到13 54 34 14 26 40。
令其等边出现，则你得到28 53 20，
即高度26 40的城门的内部对角线长。
所以你做到了。
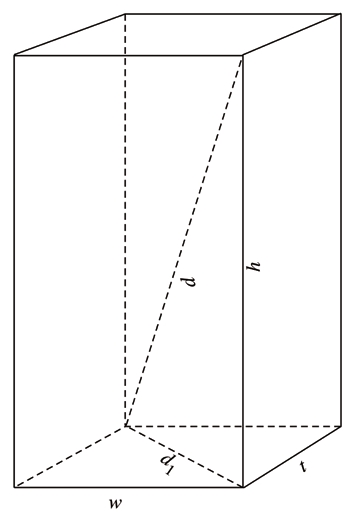
图2 泥板MS 3049的示意图
以上翻译出自弗里贝格（Jöran Friberg）的《一套非凡的巴比伦数学文献》（ A Remarkable Collection of Babylonian Mathematical Texts ），图2是他对计算所做的图解。请注意，这些数字使用的是六十进制（所以“6 40”意味着6×60+40=400），“叠上”（heap them）表示加，“使自噬”（let eat itself）表示求平方，而“等边”（likeside）是指平方根。
附带一提：另一块泥板普林顿322（Plimpton 322，见图3）常被作为美索不达米亚人已经知晓毕氏法则的证据。它包括一份数对（ s ， d ）的表格，其中 d 2 - s 2 恰是一个（有限位数的）六十进制数字（ s ， l ， d ）的平方，换句话说，即“毕氏三元数”（ s ， l ， d ）。由于泥板所列的三角形的角度是由44°稳步递减到32°的，因此人们认为它相当于一张正弦表，或者可能是一本土方工程手册，用于给出测量员可以放样的简单距离。然而，罗布森（Eleanor Robson，1969—）另有看法。在2001年10月的《美国数学月刊》（ American Math Monthly ）上，她认为这只是一张倒数数对（ x ，1/ x ）及其和与差的表格（现在因为泥板破损而不全），数字化成简单的六十进制形式，以便出数学题时使用。换句话说，这是一份教师手册。表格与三角形有关的暗示，只在于数字 d 栏的标题写着“对角线”。但史柯恩珍藏MS 3049的古巴比伦泥板明确地使用了两次毕氏法则。
图3 泥板普林顿322
是谁想出了毕氏法则？毕竟它可以说是人类发现的第一个“非平凡”的数学定理。我们知道当时有训练书吏的学校，里面的学徒要接受读、写、算的训练，这些当时都是高技能职业。（附带一提：除了颇有难度的六十进制算术，写也是一大挑战，因为当时的文字混合了苏美尔人的表意文字以及阿卡德人的音节字母，情形犹如现在的日文混合了汉字和假名。）数以百计被丢弃的学生泥板留存到现在，许多还带有错误！从这些学校毕业的书吏可以担任官僚、会计、测量员或教师。但我认为，有些书吏必定也具有数学天赋，否则不可能发现毕氏法则。我们是否应该认为他们是史上最早的数学家？这一点会有些争议。对罗布森而言，这些都是针对工程、行政和教学需求而产生的——用于测量和设计运河、土方工程等。她宣称，把他们当成数学家，是一种忽略了他们所处社会的时空错乱的说法。
这或许反映了纯粹数学与应用数学之间长久以来的紧张关系，许多工程师其实是数学天才，但数学天才并不一定就得当职业数学家，而且把当时的人称为数学家似乎有点牵强。遵照希伯特的教诲，我们不妨想象当时有位杰出的行政官员，他白天的工作是测量田地或建筑用地，并用泥板记录相关的平面图。这些几何图形或许激发了他的想象力，于是他开始探索这些图形如何界定长度和面积（人们可能会想到在瑞士专利局上班的爱因斯坦）。然而，毕氏法则是如何被发现的呢？这是真正的谜团。霍伊鲁普在《长、宽、面：古巴比伦代数及其相关知识》（ Length，Width，Surfaces: A Portrait of Old Babylonian Algebra and Its Kin ）一书中分析泥板Db 2 146 [1] 时主张，巴比伦人发现了中国西汉著名弦图的某一个版本（讨论见后）。这张弦图的关键是在一正方形内作一内接正方形，使其四角所余三角形都与给定的三角形相等。可惜的是，在泥板里找不到任何类似的图形，然而泥板BM 15285（见图4）上可以看到转成45°的内接正方形。一旦画出这种图形，就有许多方法可用于证明毕氏法则。霍伊鲁普仔细分析泥板Db 2 146的语句之后，在书中画出了一个类似弦图的图示（参见该书第259页，图67）。图5是我最偏爱的一个版本，其中A、B、C表示三个正方形的边长，也即白色三角形的三边的长。
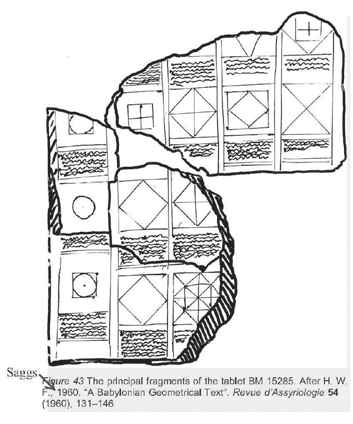
图4 一幅古巴比伦泥板BM 15285的图画，充满了许多基本的几何图形
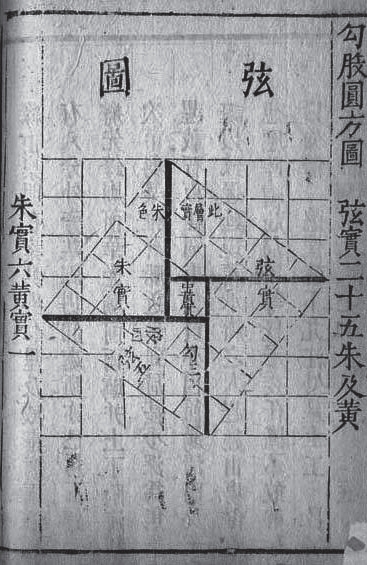
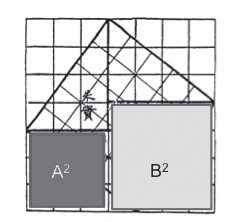
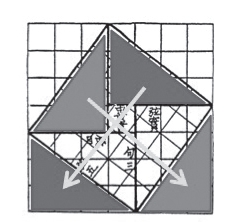
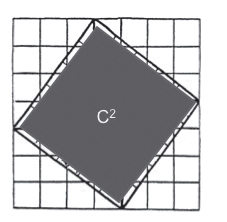
图5 弦图与毕氏定理证明（见文后彩插）
这样的猜测似乎有过度推论的嫌疑，但既然史柯恩珍藏MS 3049确切表明巴比伦人知道毕氏法则，我认为我们必须思考其可能性。然而，其他文明是否也独立发现了毕氏法则？未必见得。若我们同意毕氏法则及其相关几何学对征税和建筑物非常有用，它的知识自然会传播到与美索不达米亚有定期贸易往来的邻近文明。任何地方都需要建筑大师和测量员，有些人可能会移居他乡。古埃及和印度河流域文明的兴盛与古巴比伦大致同时，他们可能从古巴比伦那里学习了最新的技术。遗憾的是，两者的遗留物都远比两河流域少，我们难以从中推测出他们知道什么。在古埃及，所谓的“蝎王杖头”（Scorpion Macehead）年代大约在公元前3000年，上面显示法老在泛滥之后的尼罗河边播种。为土地重新定界的是“张绳者”（rope stretcher），从当时的绘画中可以看到，打上结的绳索是他们的主要工具。人们一般认为，他们使用边长3—4—5的三角形定出直角，以供工程之用。但现有的唯一证据是《柏林纸莎草书6619》的第一个问题，其中涉及解方程组 x 2 + y 2 =100， y / x =3/4。根据伊姆豪森（Annette Imhausen，1970—）的文章《埃及数学史学的传统与迷思》（“Traditions and Myths in the Historiography of Egyptian Mathematics”，《牛津数学史手册》，第791页），就现存的数学纸莎草来判断，难以认定埃及人知道一般的毕氏法则。而且，吉萨大金字塔之类的建筑物早在上述泥板出现之前800年就建成了。我的猜测是：在古王国时期，埃及人用绳索做出各边相等且对角线相等的四边形，借此构造出正方形。在中王国时期，用有结绳索以3∶4∶5的比例来构造直角三角形的方法可能已从古巴比伦传入，但其理论背景可能未传入。
至于印度河流域文明，现存3700份铭文，其中包括大约400个符号，但因为这些文字仍无法被解读，所以于事无补。然而，苏美尔文献中提到他们与东方一个叫“梅卢哈”（Meluhha）的地方有贸易往来，一般认为梅卢哈就在印度河流域，而且在印度河流域和美索不达米亚发现了完全相同的黏土印章。他们城市的街道规划非常规整，显示他们需要很好的测量技术（各种田地也需要这一技术）。然而，让整个毕氏法则由外传入的说法更为可信的，是因为毕氏法则在印度吠陀时期明确出现在《包达耶那绳法经》（ Sulba Sutra of Baudhayana ，一般定年在公元前800年）中。在此，毕氏法则不是用于规划田地、街道或建筑物，而是用于规划祭祀用的火祭坛。一般认为，印度西北部的吠陀入侵者在印度河流域文明的晚期占领了印度河流域，然后向东扩散。关于他们如何与当地居民互动或通婚，以及他们从原住民那里学到了什么，一直有很大的争议。先不论你对这些敏感问题持何种立场，令人惊讶的是，我们在吠陀经文中不仅发现了毕氏法则，而且发现了美索不达米亚、古埃及（可能还包括印度河流域）使用绳子的基本几何结构：请参考图6，若将《包达耶那绳法经》与讨论美索不达米亚泥板上的几何学的书对照来看，两者的相似程度令人吃惊。你或许会纳闷儿，吠陀信徒为何会那么在意面积？有一个很简单的仪式理由：如果献祭没有达到目的，仪式必须重新举行一次，而且祭坛面积要以（ n +1）/ n 的比例加大，以增加 n 的值。若使用毕氏法则，用绳子就很容易办到。我们也在稍后的孔雀王朝时期发现了如何运用毕氏法则的详细描述。总而言之，我们可以合理推测，大量的数学是由印度河流域的人传播给吠陀印度人的。
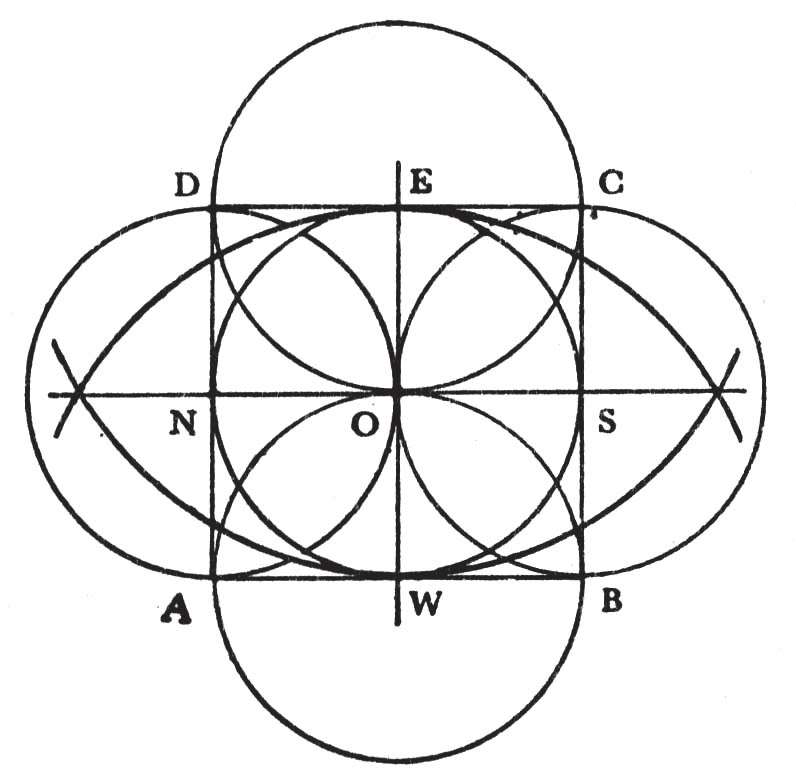
图6 在建造吠陀火祭坛之前，根据《包达耶那绳法经》的资料通过绳索绘制的圆圈图
那么，中国呢？中国数学史的一个关键问题是，数学与数学家在中国文化中的地位一向不重要。数学是低阶官员的工具，在许多朝代里，数学甚至不是科举考试的科目。天文学与占星术倒还拥有较高的地位，但在儒家思想中，这些都比不上诗歌和散文。历经秦朝的焚书坑儒后，汉朝学者能够重建先秦的许多朝代史和儒家典籍，至于数学，则只留下了它的最终状态，而没有历史源流。尽管如此，毕氏法则在他们的重构下仍浮现出完整的面貌。在汉朝的重要数学文献《九章算术》中，毕氏法则占了整整一章。使用弦图的毕氏法则证明则以略显含糊的形式，出现在《周髀算经》里。
毕氏法则以及用高斯消元法和负数解线性方程组，都是在汉朝的创造活动大爆发时被发现的吗？远在秦汉之前的一千多年里，中国文化已经扩展并建立了复杂的社会，具备成熟的政府组织和土方工程等。孔子和墨子等有科学倾向的哲学家生活在此前约300年之前。虽然我们没有直接证据，但比较合理的推测是，毕氏法则是在周朝（前1046—前256年，分为西周和东周，东周又分为春秋和战国两个时期）的某个时间被发现的。此外，毕氏法则也不太可能会在这些早期阶段从中东传入。中国文化有其独特的文字系统和奠基神话。在我看来，最有可能的是，某位不知名的数学天才在西周早期发现了这个法则。
猜测到此为止。我的中心论点是：首先，早期数学是应用数学，与日常事务紧密结合，尤其是会计和测量；其次，这些领域的算法不但可以由发现者向外传播，也可以借由实际操作者（官员、书吏、建筑大师等）散播到其他文化；第三，对于其中一些专家，他们发现的数学有了自己的生命，他们把事物推向了更深的层次，他们的发现，例如毕氏法则，应该被视为如同金属和轮子之类的重大发明。我认为，将这些人称为数学家并非时空错乱，而且我相信，当他们得到新发现时，他们的感受与我们现在的数学家并无二致。
（赵学信 译）
[1] Db 2 146是发掘编号，它的收藏编号是IM 67118。它的数学问题是已知矩形面积和对角线长，求矩形的长、宽。——译者注