1.匹配理论的基本思想

匹配问题研究的是如何将两类完全互斥的行为主体中的个体相互结合。这要求：第一，结合必须发生在两类不同的主体之间，而不是某一类主体的内部；第二，每一类主体内个体相互之间有差别（即异质性），每一个行为主体对于另一类行为主体中的每一个个体存在严格的偏好。

1.1　元模型：婚姻匹配

婚姻是最典型的匹配问题。婚姻的结合发生在男性群体和女性群体的个体之间，而且男性个体和女性个体是千差万别的，每一个男性对女性都有一个严格的偏好顺序，反之亦然。

我们通过下面的例子来说明。

例1.1 。在一个婚姻市场上有两男两女。两位男性分别被称为“虎爸”“猫爸”，两位女性分别被称为“虎妈”“猫妈”。男性和女性分属不同的群体，每位男性或女性寻找与另一个群体中的一位相结合，即匹配。每一个个体对对方个体的偏好如表1所示：

直观来看，每一种性格类型的个体都偏向于与之互补性格的异性。此外，还要注意到每个个体保持单身依然是一种选择。

1.1.1　稳定匹配

匹配问题的分析目标，或者说合理的解，就是达成稳定匹配（Stable Match-ing）。我们定义稳定匹配是这样一种匹配结果：（1）没有任何一个群体中的任何一个已经得到匹配的个体选择不匹配会更好，（2）没有任何分属两个群体的两个个体重新匹配会使得两个个体更好。也就是说，一旦达成稳定匹配结果，就不会有任何一个男性或任何一个女性愿意改变现有的匹配结果（包括单身）。与此同时，我们把使得上述条件不成立从而使得匹配不稳定的男女配对称为阻遏对（Blocking Pairs）。广义来说，阻遏对的一边可以是异性，也可以是单身（即空集）。通常所称的阻遏对则是指某个男女配对。

在上述例子中，是否存在稳定匹配呢？我们来简单分析一下。不难看出，任何包括单身的匹配结果都不是稳定的。这样就只剩下了两种匹配结果，分别是：

第一种：（虎妈，虎爸），（猫妈，猫爸）

第二种：（虎妈，猫爸），（猫妈，虎爸）

很容易验证，只有第二种结果是稳定匹配。在第一种结果下，所有的匹配对（即夫妻）都愿意和另一对夫妻中的异性重新匹配，导致100%的离婚率（和再婚率）。而第二种情况，找不到任何一对异性愿意重新组成家庭，也没有任何一个人愿意进入单身行列。

一个最核心的理论问题是：稳定匹配是否一定存在？如果存在的话，是否有简单的办法能找到？盖尔和沙普利（1962）的文章给出了肯定的回答：稳定均衡一定存在。他们提出了一种被称为延迟接受（Deferred Acceptance）的算法来找到稳定均衡，该算法又被称为盖尔-沙普利（GS）算法，以下我们称之为DA-GS算法。

我们以婚姻问题为例来解释这个算法。该算法本身又分为两种：男性提议的DA-GS算法、女性提议的DA-GS算法。我们以男性为例，算法为：

第一步：每一个男性向其最心仪的女性提出邀约。

第二步：收到邀约的女性选择其中最心仪的男性予以暂时接受。

第三步：被拒绝的男性向其第二心仪的女性提出邀约。

第四步：收到邀约的女性选择迄今所有邀约中最心仪的男性予以暂时接受。

……

直到市场上没有新的邀约发出，这发生在所有男性的邀约都被接受，或者虽然某些男性的邀约没有被接受，但他们提出的所有邀约都已被拒绝。此时每个女性持有的邀约成为最终匹配对象。

不难想象，这个算法一定会有一个终点。因为男性和女性群体的人数是有限的。盖尔和沙普利（1962）证明这个算法导致的匹配结果一定是稳定的。

将该算法用在上述例子上。

第一步：虎（猫）爸向猫（虎）妈提出邀约。

第二步：猫（虎）妈暂时接受虎（猫）爸的邀约。

没有新的邀约。算法结束。

即得到稳定匹配方式：（虎妈，猫爸），（猫妈，虎爸）。

有趣的是，他们还证明，这个算法导致的匹配结果，在所有可能的稳定匹配中，是对所有男性最有利的。相反，如果考虑一个让女性提议的DA-GS算法，则会得到一个对女性最有利的稳定匹配。在我们上面这个例子里，只有一个稳定匹配，因此无法呈现这一点。为此，我们稍微改变上面的例子。

例1.2 。个体偏好修改如表2，其余同例1.1。

我们用加粗的字体表示和上一个例子不同的偏好。现在，男性个体依然喜欢互补（或相反）性格的女性，但女性更加喜欢相同性格的男性。不难得出，此时男性提议的DA-GS算法的匹配结果是：{（虎妈，猫爸），（猫妈，虎爸）}。女性提议的DA-GS算法的匹配结果是：{（虎妈，虎爸），（猫妈，猫爸）}。容易看到：第一，两个匹配结果都是稳定的；第二，第一个匹配结果是稳定匹配中对男性最有利的，第二个匹配结果是稳定匹配中对女性最有利的（一共只有两个稳定匹配结果）。

在有更多男性和女性的婚姻匹配问题中，可能存在更多的稳定匹配。因此，稳定匹配构成了一个稳定匹配集合。接下来的问题是，这些稳定匹配相互之间是什么关系？或者说，稳定匹配存在什么样的结构？罗斯和索托马约尔（Roth and Sotomayor，1990）的著作对这个结构做了描述：所有的稳定匹配构成了一个数学上称为格（Lattice）的结构。格可以看作一个“扩展”的一维结构。在其中一端，是对所有男性最不利同时也是对所有女性最有利的稳定匹配，可以通过女性提议的DA-GS算法得到；在另一端，是对所有女性最不利同时也是对所有男性最有利的稳定匹配，可以通过男性提议的DA-GS算法得到。所有的稳定匹配都处于这两个“端点”之间，构成在一维空间的一个排序。不过，这个排序是不完全的：并不是所有的稳定匹配都完美地落在这个一维空间上，有一些稳定匹配相互之间不存在所有男性或女性都一致偏好某一个的情形。

可见，婚姻问题（一对一匹配问题）具有非常精巧的解的结构。为了进一步说明这一点，我们再来阐述这个解的结构带来的一个有意思的结论。再次修改例1.2如下。

例1.3 。增加男性和女性各1人。个体偏好修改如表3，其余同例1.1。

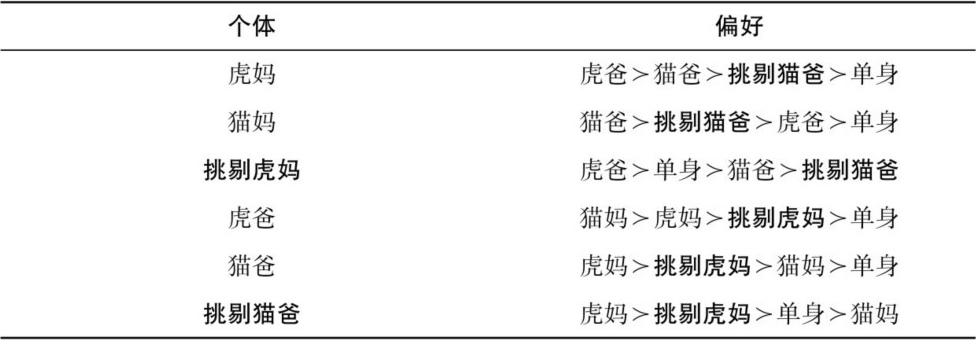
在这个例子中，加入了两位新人：挑剔虎妈和挑剔猫爸。挑剔虎妈只愿意和自己性格相同的人结婚，挑剔猫爸只愿意和自己性格相反的人结婚。此外，每一个男性和女性在同一种性格类型中，更青睐不挑剔的异性。在例1.3中，稳定匹配有哪些呢？

首先，我们注意到挑剔虎妈唯一能接受的对象是虎爸。因此，如果存在一个挑剔虎妈不为单身的稳定匹配，必定有（挑剔虎妈，虎爸）这样的匹配。

但是，这样的匹配必定被如下的匹配阻遏（虎妈，虎爸）。因为虎妈最喜欢的就是虎爸，而虎爸得到虎妈至少比得到挑剔虎妈更好。由此说明，在任何稳定匹配中，挑剔虎妈必定单身。如此，我们可以把挑剔虎妈从“市场”中去掉，得到如下简化的偏好表4：

再来看挑剔猫爸。如果在稳定匹配中他不是单身，则必然有（虎妈，挑剔猫爸）这样的配对。不难发现，（虎妈，猫爸）会阻遏上述配对。这是因为虎妈更喜欢猫爸胜过挑剔猫爸，而猫爸最喜欢的就是虎妈。由此，在任何稳定匹配中，挑剔猫爸黯然退出市场。

据此进一步简化偏好表4，就回到了前面只有虎妈、猫妈、虎爸、猫爸“四人世界”的例子（即表2）。因此最终有两个稳定匹配：稳定匹配1为{（虎妈，猫爸），（猫妈，虎爸），（挑剔虎妈），（挑剔猫爸）}；稳定匹配2为{（虎妈，虎爸），（猫妈，猫爸），（挑剔虎妈），（挑剔猫爸）}。在任何一个稳定匹配中，挑剔虎妈和挑剔猫爸都是单身。

罗斯和索托马约尔（1990）证明，在任何一个稳定匹配中，单身的个体永远单身（也就意味着，结婚的个体永远结婚）。这是一个令人惊讶的结论。这一结论引申到多对一匹配，就是著名的“乡村医院定理”（Rural Hospital Theorem）。

婚姻匹配还有一些有趣的性质，这里不再一一论述，仅再举一列。如果我们增加男性的人数，即市场中涌入更多的男性，可以证明，在给定的对男性最优或者对女性最优的稳定匹配下，女性普遍会变好，而男性普遍会变坏。类似于市场供求理论，某一方供给增加，则供给者整体受损，而另一方（需求者）受益。

稳定匹配的福利性质。 根据研究方法的不同，经济学可分为实证经济学和规范经济学。比如，市场均衡是一个实证经济学的概念，论证其存在性是一个实证经济学问题。而效率是一个规范经济学的概念，论证市场均衡实现了帕累托最优是一个规范问题，也被称为福利经济学问题。在匹配理论中，这种区分并不是很明显。一方面，我们看到，稳定匹配更像是一个规范概念，它是从界定匹配结果是否具有某种福利性质开始的。另一方面，正如盖尔和沙普利（1962）的文章论证的，这一结果也是DA-GS算法得到的一个“实证”结果。不过总体来看，稳定匹配还是更偏向于一个规范的结果，因为在现实中，并不是所有算法都会导致这一结果。

本文不打算对稳定匹配的（其他）福利结果进行过多讨论。罗斯和索托马约尔（1990）证明了，在婚姻匹配中，稳定匹配和其他福利概念，例如帕累托最优、核（Core）的概念是完全一致的。当然，在更加复杂的匹配中，这种一致性可能不能完全实现。

1.1.2　策略性行为

以上分析说明稳定的婚姻匹配一定存在，并可以通过DA-GS实现。这似乎是一个一劳永逸的答案。不过，当一个婚姻市场的设计者想要采用这一算法来实现稳定匹配时（对男性或者女性最优），我们有理由询问，男女双方有真实报告自己偏好的激励吗？机制设计是希望人们说实话的，即所谓的激励相容（Incentive Compatibility，以下简称IC）。如果参与者在给定机制下没有真实报告自己偏好的激励，那么上文论述的稳定匹配可能会被破坏。或者说，稳定匹配只针对报告出来的偏好是稳定的，对于隐藏的真实偏好可能并非如此。此外，相对于存在“谎报”的机制而言，真实报告的机制还有其他优点：它可以极大地节省人们为了自身利益而采取策略性行为付出的努力，以及由于未能正确选择合理的策略性行为而导致不尽如人意的匹配。

我们首先说明，在一个男性提议的DA-GS算法中，女性可能没有报告真实偏好的激励。重新考虑例1.2。我们已经知道，在所有人都报告真实偏好时，男性提议的DA-GS算法的匹配结果（也就是男性最优的稳定匹配结果）是：{（虎妈，猫爸），（猫妈，虎爸）}。显然，在这个结果下，女性没有得到自己最满意的选择（见表2）。现在考虑女性谎报自己的偏好如下：

虎妈的假偏好：虎爸＞单身＞猫爸。

猫妈的假偏好：猫爸＞单身＞虎爸。

再次使用男性提议的DA-GS算法，此时的匹配结果为：{（虎妈，虎爸），（猫妈，猫爸）}。女性通过谎报自己的偏好，使自己获得了更为满意的结果。罗斯和索托马约尔（1990）通过举出反例证明，不存在一个导致稳定匹配的机制，使得所有人都真实报告其偏好。

这似乎是一个悲剧性的结论。但值得庆幸的是，在男性提议的DA-GS机制中，男性真实报告其偏好是他的弱占优策略，即有真实报告偏好的激励。这一结论依然有重要意义，因为在某些匹配中，我们可以通过其他制度保证一方不会谎报，比如在大学录取中，大学的录取标准是透明的，同时也受到监督，我们只需要担心学生一方是否有谎报的激励。此时，单边激励相容的机制（此处即学生提议的DA-GS机制）就可以很好地保证参与者的利益最大化。

1.2　大学录取

我们接下来讨论大学录取这一典型的“多对一”匹配问题。它包括两个完全互斥的行为主体：大学和学生。学生对不同的大学有偏好。大学对不同的学生也有偏好，大学的偏好可能来自自身，也可能来自政策规定。一个大学可以录取多个学生，但一个学生最多只能上一所大学，即多对一匹配。此外，大学录取不存在可以谈判的货币转移：虽然有学费，但金额是固定的，它不能自由调节以改变学校和学生的匹配效用。

1.2.1　大学的响应性偏好

大学录取和更为一般的多对一匹配的关键假设是刻画大学的偏好。我们需要刻画大学对所有学生群体的偏好，而不仅仅是对学生个体的偏好。我们首先考虑简单的情况，即大学基于对个别学生的偏好，以某种方式来决定录取。为此，我们假定大学对单个学生存在一个确定的、理性的偏好排序。此外，为了反映资源的稀缺性，我们同时假定每个大学有确定的录取名额，即最多可以录取的学生人数。在这一描述中，我们只刻画了大学对个别学生的偏好和它能够录取的最大学生数。为此，我们做出一个关键假设：大学对任何两个学生的偏好，不受大学是否录取其他学生的影响。罗斯和索托马约尔（1990）将这样的大学偏好称为对个别学生偏好“做出响应”的偏好，简称为响应性偏好。

我们用下面的例子来具体说明响应性偏好。假定一共有3名学生1、2、3。同时假定大学有3个录取名额。大学对他们的偏好为1＞2＞3＞。这里代表大学一个空缺的席位，大学对于任何一个学生都是“可以接受”的，即好于空缺。首先，响应性偏好认为：{1}＞{2}＞{3}，即大学可以比较单个学生组成的“学生群体”。接下来，我们来考虑{1，2}和{3}这两个学生群体的比较。我们的结论是：{1，2}＞{3}。这只需要注意到{1，2}＞{1}＞{3}。其中，前半部分由响应性偏好的定义保证，即两个学生集合如果不相同的部分可以比较“优劣”，则两个集合整体可以比较。这里{1，2}和{1}不相同的部分是2＞。我们也有：{1，3}＞{2}，因为{1，3}＞{1}＞{2}。值得注意的是，响应性偏好并未完整刻画大学对学生群体的偏好。考虑有4个学生1、2、3、4。大学偏好为1＞2＞3＞4，则{1，4}和{2，3}不能根据响应性偏好推出比较结果。

虽然响应性偏好未能完整刻画大学对全部学生群体的偏好，但这一刻画却足够细致，以至于可以判断某一个匹配结果是否稳定。

我们下面的分析将基于上述对大学偏好的假设，即响应性偏好。由于大学和学生的非对称性，我们先分别讨论对学生最优的稳定匹配和对大学最优的稳定匹配，我们将会看到他们有一些重要的差别。然后再来一般性地讨论所有稳定匹配的性质及其相互关系。

1.2.2　对学生最优的稳定匹配

与婚姻匹配类似，我们可以构造一个学生提议的DA-GS算法：

第一步：所有学生向其最心仪的学校发出邀约。

第二步：所有学校在向其提出邀约的学生中，在不多于其名额的前提下，选择最喜欢的、可接受的、尽可能多的学生予以暂时接受。

第三步：在第二步中被拒绝的学生，选择向第二心仪的学校发出邀约。

第四步：所有学校在向其提出邀约的学生中，在不多于其名额的前提下，选择最喜欢的、可接受的、尽可能多的学生予以暂时接受；其余学生予以拒绝。

第五步：在第四步中被拒绝的学生，选择向第三心仪的学校发出邀约。

……

如果所有学生的邀约都已被接受，或者那些邀约被拒绝的学生已经向所有可接受的学校都已经发出了邀约（且被拒绝），则算法结束。

罗斯和索托马约尔（1990）说明了，学生提议的DA-GS算法必定导致对学生最优的稳定匹配。同时在这个机制下，学生能够真实报告自己的偏好。这些结论和婚姻匹配的结论可以完美对照。

1.2.3　对大学最优的稳定匹配

考虑由学校提议的DA-GS机制，算法如下：

第一步：所有学校向其最心仪的、可接受的、在其名额范围内尽可能多的学生发出邀约。

第二步：每个接受邀约的学生选择可接受的邀约予以暂时接受。

第三步：所有学校在保留被接受的所有邀约的前提下，向其最心仪的、可接受的、在其（剩余）名额范围内尽可能多的学生发出邀约。

第四步：每个收到新邀约的学生选择可接受的、心仪的邀约予以暂时接受，并拒绝其他邀约。

第五步：重复第三步。

第六步：重复第四步。

……

如果所有学校的所有邀约都已经被接受，或者存在邀约被拒绝的情况的学校已经对其可接受的所有学生发送过邀约，则算法结束。

学校提议的DA-GS机制一定会得到稳定匹配，且在所有稳定匹配中是对学校最好的。令人惊讶的是，学校在此机制中并不总是说实话。这是和婚姻匹配（或一对一匹配）不同的。罗斯和索托马约尔（1990）通过反例说明了这一点。这里的关键是，对于学校而言，它拥有了向多个学生同时提出邀约的权利。这给予了它更大的“操纵”空间，从而有更大的激励（包括更多的方式）说谎，比如，它现在可以通过少于其剩余名额的方式提出邀约。

1.2.4　所有的稳定匹配

除了上述讨论的对学生最优和对大学最优的稳定匹配，大学录取问题还可能存在其他的稳定匹配。类似于婚姻问题，所有的稳定匹配也构成了一个格的结构。格的一端是对学生最优的稳定匹配，同时也是对大学最差（或者说最不偏好）的稳定匹配，另一端是对大学最优的稳定匹配。中间的稳定匹配可以从对学生更有利到更不利进行排序（并非所有稳定匹配都可以比较，但总是能将稳定匹配分组，使得组内不能比较，组间可以比较，这也是格的定义），同时这一排序也对应着从对大学更不利到更有利的排序。注意，我们刻画的大学的偏好并不能对所有的学生群体排序，但在稳定匹配之间，仅仅根据响应性偏好也是可以排序的。

我们在婚姻问题中证明了“乡村医院定理”。在大学录取中，该定理依然成立，即在所有的稳定匹配中，被大学录取的学生群体是相同的（但录取的学校可能不同）。同时，大学录取的学生人数也是相同的，也就是说，录满（即用完全部配额）的大学总是录满，未录满的也总是未录满，且未录取的“空额”也是相同的。更有甚者，罗斯和索托马约尔（1990）的研究表明，对于未录满的大学而言，在所有的稳定匹配中，它们录取的学生群体（不仅仅是人数）是完全相同的。中国有些冷门大学经常有录不满人的情况，按照这一结论，无论如何改变算法，只要还是稳定匹配，不仅这些大学永远录不满，甚至想提高录取学生的质量都是不可能的。

同样，我们也可以证明，类似市场供求理论，如果在大学录取市场上有更多的大学进入，则在对学生最优的稳定匹配下，学生的福利总是提高的，而大学的福利总是下降的。反之，如果有更多的学生进入，则在对大学最优的稳定匹配下，大学的福利总是提高的，而学生的福利总是下降的。

1.2.5　更为一般的大学（或机构）偏好

在上述论证中，对大学偏好的假设起到了非常关键的作用。我们在一开始就提到，像大学录取这样的多对一匹配问题，区别于婚姻问题的关键就是大学（或机构）这一方。由于大学匹配的对象是多个人的集合，因此其偏好更为复杂。上述分析表明，如果大学的偏好满足响应性条件，关于婚姻匹配的大部分结论对大学来说也是成立的，当然也存在一些重大区别。比如，在对大学最优的稳定匹配（即大学提议的DA-GS机制）下，大学不再说实话。

显然，大学的响应性偏好是一个比较特殊的条件。很多时候，机构（包括大学或者公司）并没有固定的需要录取或雇佣的人数，有时候录取对象不是逐个比较的。考虑这样一个简单的例子。一个大学有两个名额，有四个学生申请，大学对各个学生的偏好为：计算机专业学生1＞计算机专业学生2＞社科专业学生1＞社科专业学生2。按照响应性偏好，必然有{计算机专业学生1，计算机专业学生2}＞{计算机专业学生1，社科专业学生1}。但如果学校偏好专业多样性，即它不愿意同时录取两个相同专业的学生，那么，它的偏好很可能反过来，即{计算机专业学生1，社科专业学生1}＞{计算机专业学生1，计算机专业学生2}。这就违背了响应性偏好。

那么，接下来我们要问：假定大学的偏好不再是响应性偏好，会在多大程度上影响我们的结论呢？哈特菲尔德和米尔格罗姆（Hatfield and Milgrom，2005）的研究深入思考了这个问题，在更一般的带有合同的匹配（Matching with Contracts）框架下，他们提出了两个包含响应性偏好的更一般的大学偏好性质，即可替代性和总需求定律，我们来逐一说明这两个性质。

可替代性 。假定学校面对两个学生群体X和X′，后一个群体包含前一个群体，即XŽX′。我们定义大学对学生群体的偏好满足可替代性，如果在前一个（小）群体未被大学录取的学生，在后一个（大）群体中也不能被录取，即R（X）ŽR（X′）。这里R（X）表示在学生集合X中被大学拒绝的学生子集。显然，R（X）=X-C（X）。这里C（X）表示在X中被大学录取的学生子集。直观地说，在可替代性条件下，如果某个学生被拒绝，则增加一些“同伴”并不能使得该学生被留下。

我们举两个简单的例子来帮助读者更好地理解这个概念。在第一个例子中，我们来观察一个消费者的偏好是否符合可替代性。有两个消费者：张三和李四。张三考虑在三种水果之间的偏好，而李四考虑对咖啡+糖和茶之间的偏好。

张三：苹果＞梨＞橘子，且不喜欢混着吃。

李四：咖啡+糖＞茶＞咖啡。

显然，张三的偏好满足可替代性。实际上，张三的偏好和婚姻匹配中人们的偏好是一致的，在此类情景中，我们不允许同时选择两种“商品”。来看李四的偏好。我们有：{咖啡，茶}{咖啡，茶，糖}，而R（{咖啡，茶}）={咖啡}R（{咖啡，茶，糖}）={茶}。因此李四的偏好不满足可替代性。直观地说，咖啡和糖是互补性商品。因此咖啡是否被拒绝，依赖于选择集合中是否有糖。

再来看下面的例子。梁山泊公司对仅有的两条好汉张顺、李逵有如下偏好，而清风寨公司对仅有的两条好汉张青、孙二娘有如下偏好：

梁山泊：{张顺，李逵}＞{张顺}＞{李逵}＞不雇人。

清风寨：{张青，孙二娘}＞不雇人＞{孙二娘}＞{张青}。

显然，梁山泊公司的偏好具有可替代性，而清风寨公司的偏好不具有可替代性。

值得注意的是，婚姻匹配中每个人的偏好都被限制在只能在单个对象间进行比较，而大学录取中我们假定了响应性偏好，即在给定名额下对录取对象逐个进行比较，这些偏好都符合可替代性。

哈特菲尔德和米尔格罗姆（2005）证明了，在大学对学生的偏好具有可替代性时，稳定匹配一定存在。同时，学生提议的DA-GS算法可以实现对学生最优的稳定匹配，大学提议的DA-GS算法可以实现对大学最优的稳定匹配。有趣的是，可替代性条件不能保证在学生提议的DA-GS下，学生是说实话的。为此，我们还需要一个总需求定律的条件。

总需求定律 。仍然考虑两个学生群体X和X′，XŽX′。大学对学生的偏好满足总需求定律的条件：|C（X）|≤|C（X′）|。直观地说，随着学生群体的扩大，被接受的学生人数是增加的，至少不是下降的。

注意，总需求定律不等于可替代性。考虑如下的“三人”大学偏好：

“三人”大学：{学生3}＞{学生1，学生2}＞{学生1}＞{学生2}＞＞{学生1，学生3}＞{学生2，学生3}＞{学生1，学生2，学生3}。

容易验证这一偏好满足可替代性，但并不满足总需求定律，因为：|C（{学生1，学生2}）={学生1，学生2}|=2＞|C（{学生1，学生2，学生3}）={学生3}|=1。反过来，满足总需求定律也可能不满足可替代性。例如，从上述清风寨公司的偏好，我们知道是不满足可替代性的，但|C（{张青或孙二娘}）=|=0≺|C（{张青，孙二娘}）={张青，孙二娘}|=2，满足总需求定律。

哈特菲尔德和米尔格罗姆（2005）证明，只有在可替代性和总需求定律同时满足时，在对学生最优的DA-GS算法下，学生才是说实话的。证明中关键的一点是，只有在这两个条件下，“乡村医院定理”才能满足。而在我们对婚姻匹配的分析中已经看到，这个定理对于保证参与者（男性和女性是完全对称的）说实话是至关重要的。

总需求定律和可替代性是两个互相区别但又有联系的概念。在哈特菲尔德和米尔格罗姆（2005）的研究中，他们也发现，在一些特殊情形下，二者具有某种等价关系。如果我们仔细来思考这两个条件，会发现“可替代性”更类似于排除了“正向的”互补关系。例如，在上述张青和孙二娘（或咖啡和茶）的例子中，对象之间都存在正向的互补关系，从而不具有可替代性——当增加他们的“搭档”之后，他们更加有吸引力，因而其结果会从被拒绝变成不被拒绝。而总需求定律更类似于排除了“负向的”互补关系。

为此，考虑下面的例子。在新梁山泊公司里，李逵是一个非常能干却无法和同事共处的人。因此有：

新梁山泊：{李逵}＞{阮小二，阮小五}＞{阮小二}＞{阮小五}＞＞{阮小二，李逵}＞{阮小五，李逵}＞{阮小二，阮小五，李逵}。

不难发现这个例子和上述“三人”大学的例子是完全同构的。根据刚才的分析，它不满足总需求定律，因为：|C（{阮小二，阮小五}）={阮小二，阮小五}|=2＞|C（{阮小二，阮小五，李逵}）={李逵}|=1。直观地说，随着“上山”人数的增加，山寨本来有更多的人才可用，因此选择人数必定增加，至少不减少（注意，这里不要求原来选择的人员必定还能留下，只要求人数不减少。道理也很简单，假定山寨容量有限，仍然可以裁掉过去的一些人员）。但由于李逵和其他人水火不容，即存在负向的互补性，所以存在一种可能，山寨留下李逵（因为他十分能干）而裁掉其余两人。从而违反总需求定律。

1.3　匹配问题的边界

刚才讨论了两个重要的匹配问题：婚姻问题和大学录取问题。我们已经发现，这两个问题既有联系，又有区别。那么一个自然的问题是，还有哪些问题属于匹配问题呢？它们相互之间又有哪些不同的特征呢？匹配理论的极大发展，带来的一个问题就是匹配问题的边界变得越来越模糊。因此，澄清哪些问题属于匹配问题，哪些不属于，即划出一个匹配问题的边界（尽管可能仍然是模糊的），也许是必要的。

我们把婚姻问题作为匹配问题的元模型（或者说参照系），可以归纳出匹配问题的三个特征：

特征1：匹配问题必然涉及两个完全互斥的行为主体集合。

特征2：这两个行为主体都对对方（或者说，与对方达成的交易）存在一个主观评价。

特征3：匹配双方不存在货币转移，或者说，匹配双方只有一个固定的（隐含）合同。

特征1和特征2是我们一直强调的。特征3意味着，匹配双方除是否匹配之外，不存在其他谈判空间，匹配对象本身是决定交易效用的唯一因素。例如，在婚姻匹配中，我们认为不能通过嫁妆或彩礼来改变匹配的效用。

值得注意的是，如果严格按照这三个特征来界定匹配问题，那么，几乎只有婚姻问题属于匹配问题。但很多问题在不同程度上可以转换为匹配问题来分析。表5归纳了与匹配理论相关的若干典型问题，从上至下根据转换的“容易程度”排列。我们逐一加以说明，这里略过已经讨论的婚姻匹配和大学录取问题。

美国住院医生市场（NIMP） 。这是一个典型的多对一匹配问题。医生只能选择一家医院，而医院可以选择多个医生。NIMP问题和大学录取问题是极其类似的。这个问题满足匹配问题的三个特征（双边性、主体性、无转移支付）。值得注意的是医院实际上是一个机构，其偏好可能来自医院自身决策者的个人或集体偏好，也可能来自某些政策限制。

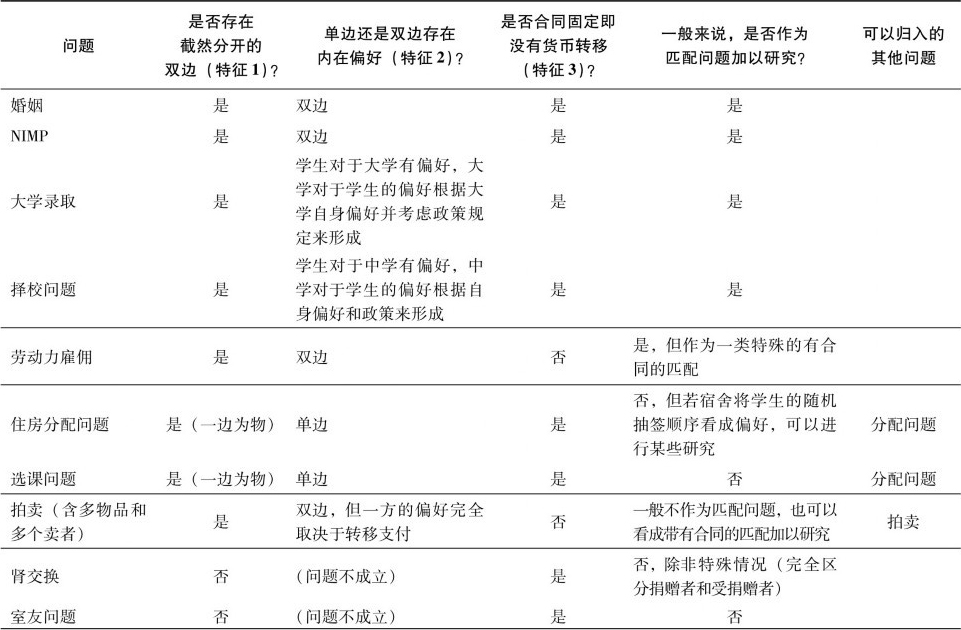
择校问题（School Choice） 。阿布杜尔卡迪罗格鲁和森梅兹（Abdulkadiro-glu and Sonmez，2003）将美国公立中小学的择校问题引入匹配理论的研究视野之中。这个问题也是一个多对一问题。但与NIMP和大学录取问题略有不同的是，学校对学生的偏好很大程度上由政策规定。一般来说，住在学校所在社区的学生或已有兄弟姐妹在此读书的学生享有优先权。这个偏好序是比较“粗糙”的，很多学生有相同的优先权，必须采用某种随机抽签的方式来“打破平局”。如何更好地解决这一问题成为研究的一个重点，感兴趣的读者可参考埃德里尔和埃尔金（Edril and Ergin，2013）的综述文章。

劳动力雇佣 。凯尔索和克劳福德（Kelso and Crawford，1982）开创了用匹配理论研究劳动力市场雇佣问题的先河。该问题依然是一个多对一的匹配问题。但有两个不同于其他模型的特点。第一，雇主对雇员的偏好比大学录取、择校或者NIMP更加复杂。一般来说，雇主对雇佣人数没有硬性限制，但为了稳定匹配的存在，要求雇主对雇员群体的偏好具有某种可替代性（参见第1.2.5节的讨论）。第二，雇主和雇员的偏好不仅受到对方是谁的影响，还受到工资的影响。雇员可能对给出高工资但“令人讨厌的”雇主更加青睐；而雇主也可能愿意花费低工资雇用一个生产率较低的员工。虽然模型假定工资只能离散取值，比如最小单位为1元，以便构建算法，但这里的关键是，工资本身仍然是可以调节的，以平衡匹配结果。

凯尔索和克劳福德构造了一个巧妙的算法以得到稳定的匹配。该算法类似于DA-GS算法，但将上述两个特殊之处考虑在内。也就是说，第一，解决雇主对雇员的偏好存在可替代性时，雇主如何提出邀约；第二，解决工资如何在邀约和反邀约的过程中得到确定。第一个问题的解决要求雇主每次对他最喜欢的“所有”雇员都提出邀约，但不能对已接受其上一次邀约的雇员“毁约”，这和大学录取中大学提议的DA-GS机制是完全类似的。第二个问题采取了类似拍卖中的升价拍卖机制。这篇文章巧妙地将拍卖问题和匹配问题的研究方法结合，极具启发性。有兴趣的读者可以阅读他们的文章，或者罗斯和索托马约尔（1990）第6章的介绍。不过，由于劳动力雇佣问题涉及了货币转移支付，我们把它看作一种处于“中间状态的”匹配问题。

住房分配（House Allocation）问题 。住房分配问题以及后面要介绍的选课（Course Allocation）问题经常被称为单边匹配（One-sided Matching）问题，也被称为分配问题（Assignment Problem）。经典的住房分配问题考虑将（无主的）房屋分给房客居住，最典型的例子就是将（单身）宿舍分配给学生。由于匹配的一边为物品，住房分配问题虽然具备双边性（特征1），但不具备双边的“主体性”：只有匹配的一边即学生对宿舍有偏好，宿舍对学生没有偏好，即不完全满足特征2，这就和大学录取、NIMP、择校等问题有较大区别。不过，阿布杜尔卡迪罗格鲁和森梅兹（1998）的经典文章仍然试图将住房分配问题和匹配问题联系起来。他们提出采用一种随机序列独裁机制（Random Series Dictatorship，简称RSD）的算法来分配宿舍：首先赋予所有宿舍对所有学生相同的偏好序——由统一的随机抽签决定，然后由排序第一的学生选定宿舍，接着由排序第二的学生来选，以此类推。不难发现，这相当于赋予宿舍由统一的随机抽签决定的学生偏好序，然后依据学生提议的DA-GS算法进行匹配。

从批判的立场来看，将住房分配问题转化为匹配问题实际上是比较勉强的。不仅“住房”对房客的偏好完全是随机导入的，而且所有房屋都有相同的偏好。而匹配问题的有趣之处恰恰在于双方都具有某种异质性偏好。在表5中，我们仍然把它视作一个处于中间的“模糊”匹配问题。

选课问题 。在一所大学中，如何设计一个选课机制，达到让学生尽可能满意的课程分配效果？这就是选课问题。和住房分配问题类似，选课问题具有双边性，但只有一边是有偏好的“主体”。在学生和课程的双边选择中，学生对课程（更准确地说，课程组合或课表）有偏好，但课程对学生没有偏好。虽然一些课程赋予某些学生优先权，但这个偏好通常是“粗糙”的。与住房分配问题不同的是，它是一个多对多匹配问题（如果看成匹配问题的话）：一个学生可以选多门课，一门课可以容纳多个学生。

一种简单的解决办法仍然是随机序列独裁机制：通过随机抽签，排名第一的学生优先选择其需要的所有课程，然后排名第二的学生来选（这里没有考虑课程有优先级，但包含了某些课程完全禁止某些学生来选）。这样得到的匹配结果虽然实现了事后的帕累托最优，但显然非常不公平，因而在实际中是难以接受的。

布迪什（Budish，2011）提出使用一种所谓“同等收入的近似竞争均衡”（Approximate Competitive Equilibrium from Equal Income，简称A-CEEI）来解决选课问题。其思路是：由学生报告对课表的偏好，然后匹配系统赋予每个学生近似的相等收入，进而计算出在给定学生课表偏好序下近似的市场均衡。该均衡包含每门课程的价格，并决定了每个学生得到的课程组合。布迪什证明这个算法具有很好的效率和公平性质。值得注意的是，这个算法“回到”了传统经济学的市场均衡概念，和匹配理论已相去甚远。

拍卖 。拍卖是经济学中得到深入研究的一类问题。某种意义上市场机制也可以看成是一种拍卖机制。无论是单一物品拍卖，还是多物品拍卖，都有和匹配问题相似的特征。拍卖是双边的：买者和卖者。通过转移支付，即价格，买者和卖者也都形成了对对方的“主观”评价：买者愿意选择带给他最高净收益（支付意愿减去价格）的卖者，而卖者愿意选择出价最高的买者。在这里，转移支付或者说价格是不可或缺的，这是拍卖问题与经典匹配问题的最大不同。此外，卖者对买者本身（除去价格）没有评价，这又不同于劳动力雇佣问题。拍卖问题和劳动力雇佣都可以看成是“带有合同的匹配”问题。哈特菲尔德和米尔格罗姆（2005）的论文提出了这一概念。带有合同的匹配几乎涵盖了所有上述的多对一匹配问题，只排除了选课和住房分配这样的分配问题。

像拍卖这一类带有转移支付的匹配问题是否应该作为匹配问题来研究？一方面，允许转移支付可能会对匹配结果产生很大的影响。“丑女嫁靓仔”（或者相反）变得可能。原有匹配理论的一些性质可能被改变。另一方面，带有转移支付的匹配问题确实具有一定的实用性，例如研究劳动力市场。从尽可能简化的问题出发，本文不将拍卖视作匹配问题（如表5）。这与纪尧姆·海宁格（Haeringer，2017）在其所著的《市场设计：拍卖与匹配》一书的处理是一致的，在该书中，匹配问题和拍卖问题被看作是市场设计的两类主要问题，但互不包含。

肾交换机制（Kidney Exchange） 。器官捐献是一类非常特殊的“资源配置”问题。器官买卖通常是被禁止的，但器官的“市场”机会始终存在。肾的器官捐献最为典型。从最简单的意义来看，肾交换是一个纯交换市场：每个肾病患者都有一个亲属捐献者，但他们二者的器官可能由于血型或器官配型不兼容，通过与其他类似的肾病患者-亲属捐献者互换可捐献的肾，无论是两两互换还是链式交换，都可能实现对双方或多方有利的交易。纯交换问题不具有匹配问题的双边属性，也不是所谓的单边匹配或分配问题，因为肾本身是有明确所有权的。因此我们不视之为匹配问题。但是，一些肾交换机制有可能转换为匹配问题。比如，某些肾是由死者甚至生者无偿捐献的，这一问题就更类似于单边匹配。还有一种情况，某些捐献者捐出肾的同时不能立即得到合适的肾，但可以得到一个优先排队权，类似于宿舍分配问题。有兴趣的读者可以参考森梅兹和云韦尔（Sonmez and Ünver，2013）对肾交换的综述文章。

室友问题（Roommate Problem） 。一个学校有若干间宿舍，每间宿舍有两个床位，需要分配给住校生（一人一间不被允许）。每个住校生对和谁成为室友具有严格的偏好序，这就是室友问题。这个问题通常都是作为匹配问题的反例提出的。因为在这个问题中，明显不存在双边性，而只有一类主体——学生（注意这里的宿舍都是同质的，人们只在乎和谁同宿舍）。有趣的是，某种稳定匹配的概念（更类似于合作博弈的核概念，此处不要求双边性）依然存在，即在某一个分配方案下，不存在未被配对的室友，他们愿意匹配在一起。不过遗憾的是，在室友问题中，稳定匹配不一定存在，可参考罗斯和索托马约尔（1990）的研究。

室友问题的特殊之处在于，任何一对学生的配对（可以理解为一次交易）都会对其他学生产生外部性，即改变其他学生的效用。在之前的所有问题中，交易不直接改变未参与交易的其他人的效用，即没有外部性。合作博弈理论发现，当存在外部性时，核可能不存在，例如在经典的“垃圾博弈”（Garbage Game）中。这也解释了为什么室友问题可能不存在稳定匹配。 4kjFnCfMWWZlj8OsIkSCFj7PgfyhlvbE0mCPOz8qmkgJSOBMC2sZ6Wonftcj1/Cu