




神经网络是一种有监督的学习,假设训练集为( x ( i ), y ( i )),那么,通过多层神经元的组合可以模拟一种复杂且非线性的假设模型 h W , b ( x ),其中, W 和 b 为待拟合的参数。神经网络对多个单一的神经元进行联结,多个神经元的输出可以同时被送到另一个神经元中作为输入,通过这种组合方式可以完成对复杂非线性模型的描述。神经网络示意图如图1-1所示。
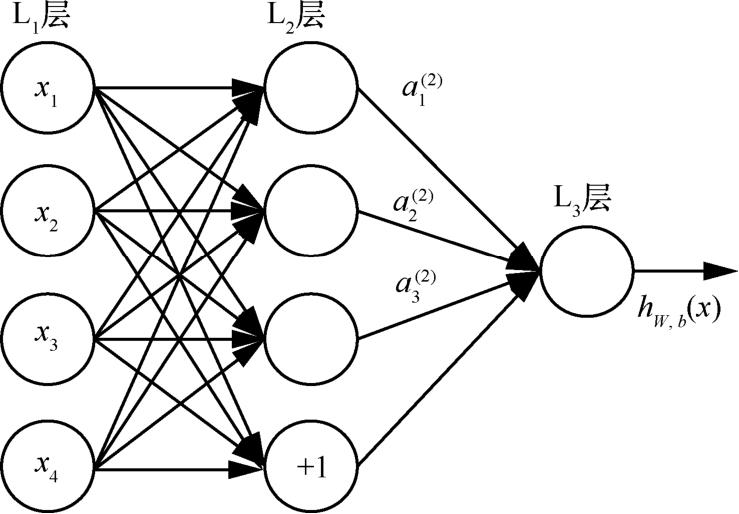
图1-1 神经网络示意图
给定一个前馈神经网络,利用下面的符号来描述该网络。
· f l (·):表示第 l 层神经元的激活函数。
·
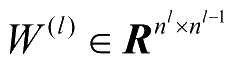 :表示第
l
-1层到第
l
层的权重矩阵。
:表示第
l
-1层到第
l
层的权重矩阵。
·
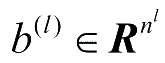 :表示第
l
-1层到第
l
层的偏置。
:表示第
l
-1层到第
l
层的偏置。
·
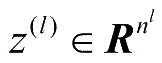 :表示第
l
层神经元的状态。
:表示第
l
层神经元的状态。
·
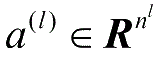 :表示第
l
层神经元的活性值。
:表示第
l
层神经元的活性值。
前馈神经网络通过式(1-1)和式(1-2)进行信息传播:

式(1-1)和式(1-2)可以合并为:

通过逐层的前馈传播,得到网络最后的输出 a L :
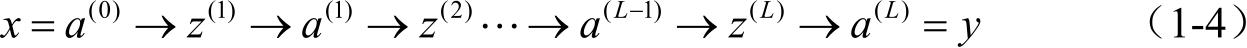
反向传播算法的思路如下,假设样本集为{(
x
(1)
,
y
(1)
),…,(
x
(
m
)
,
y
(
m
)
)},共
m
个样例,首先进行前向传播运算,计算出网络中所有的激活值,输出值记为
h
W
,
b
(
x
)。之后,针对第
l
层的每一个节点
i
,计算出其残差
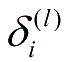 ,该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点,可以直接计算出网络产生的激活值与实际值之间的差距,将这个差距定义为
,该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点,可以直接计算出网络产生的激活值与实际值之间的差距,将这个差距定义为
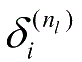 。对于网络中将
。对于网络中将
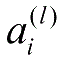 作为输入的隐藏单元,利用第
l
+1层节点残差的加权平均值计算
作为输入的隐藏单元,利用第
l
+1层节点残差的加权平均值计算
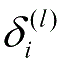 ,由此,反向传播算法的具体细节如下所示:
,由此,反向传播算法的具体细节如下所示:
(1)进行前馈传播计算,利用前向传播计算式,得到
L
2
,
L
3
,…直到输出层
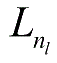 的激活值;
的激活值;
(2)对于第 n l 层(输出层)的每个输出单元 i ,根据式(1-5)计算残差( J 为代价函数):
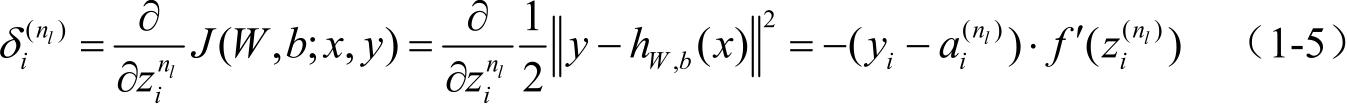
(3)对于 l = n l -1, n l -2, n l -3,…,2的各个网络层,第 l 层的第 i 个节点的残差计算式为:
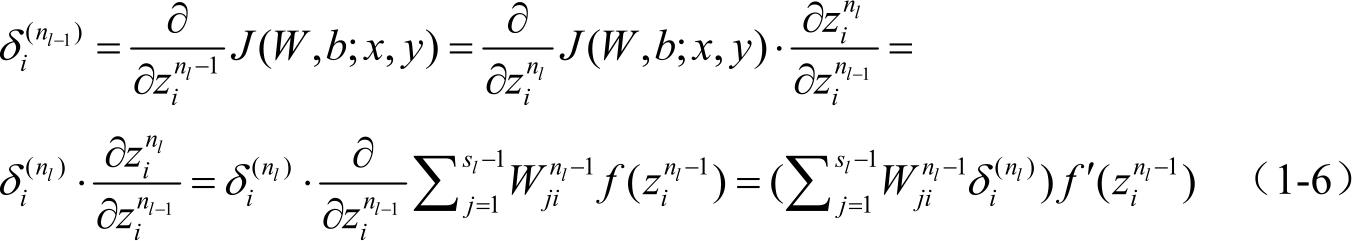
根据推导过程,将 n l -1与 n l 的关系替换为 l 与 l +1,可以得到:
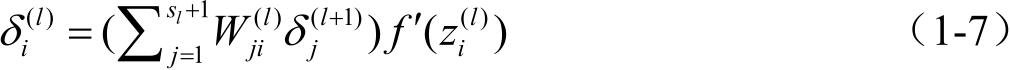
通过逐层的迭代求导计算,实现了算法的反向传播。
(4)偏导数的计算如下:
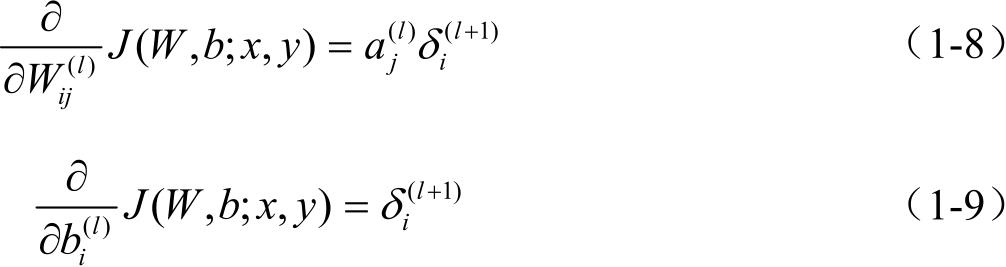
针对只包含单个样例( x , y )的网络,代价函数为:
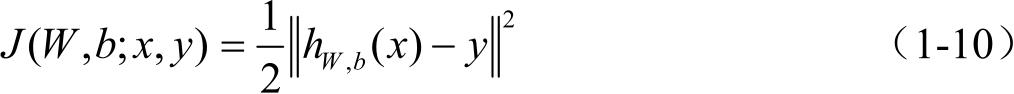
对于包含 m 个样本空间的数据集,网络的整体代价函数可定义为:
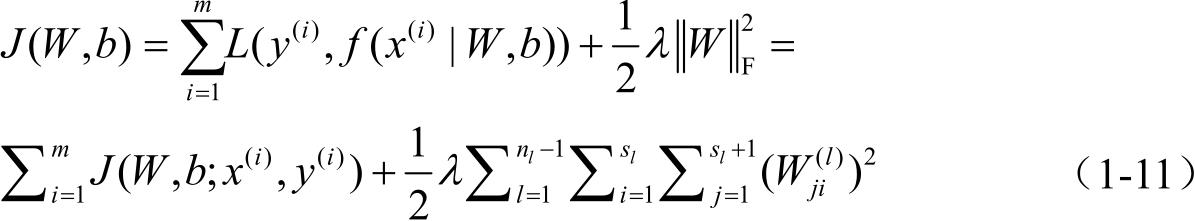
其中,系数 λ 影响式(1-11)中两项的相对权重,代价函数的优化目标是利用参数 W 和 b 通过反复迭代求取 J ( W , b )的最小值。采用梯度下降法更新参数:
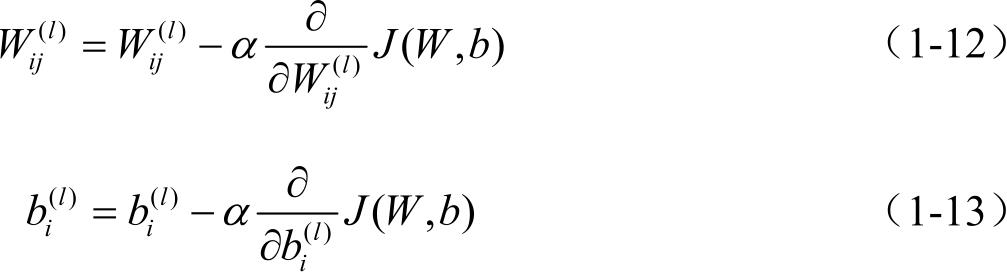
其中, α 是学习率。