下载掌阅APP，畅读海量书库
立即打开
通信的目的在于传递信息。传递信息的多少用“信息量”衡量。消息中所含的信息量 I 是信息 x 出现的概率 P （ x ）的函数，即
消息出现的概率越小，它所含的信息量越大；反之信息量越小，且当 P （ x ）=1时， I =0。若干个互相独立事件构成的消息，所含信息量等于各独立事件信息量的和，即
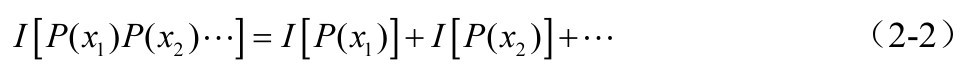
从式（2-1）可以看出，若 I 与 P （ x ）间的关系式为
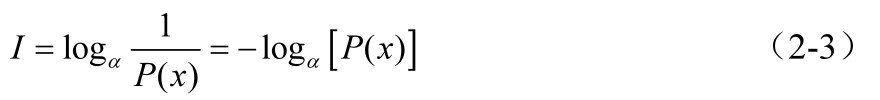
则信息量的单位取决于式（2-3）中的对数底数 α ，如果 α =2，则信息量的单位为比特（bit）；如果 α =e，则信息量的单位为奈特（nit）；如果 α =10，则信息量的单位为哈特莱。
假设离散消息的出现概率是相等的，需要传递的离散消息是在 M 个消息之中独立地选择其一，且认为每一个消息出现的概率是相同的。为了传递一个消息，只需采用一个 M 进制的波形来传送。也就是说，传递 M 个消息之一这一件事与传送 M 进制波形之一是完全等价的。 M 进制中最简单的情况是 M =2，即二进制，在等概率出现时
当 M ＞2，则传送每一波形的信息量应为
