




当温度变化时,物质的晶体结构不一定保持不变. 实际上,很多物质有所谓的同素异形变化. 例如在低温时,铁有α-Fe的形式,这是一种a=2.86Å和d=2.58Å的体心立方格子;高温时变为γ-Fe,是a=3.56Å和d=2.57Å的面心立方格子. 类似地,钴在低温的形式是α-Co,为六方密堆积结构,有a=2.51Å,c=4.11Å和d=2.51Å;高温时变成β-Co,是一种a=3.55Å和d=2.51Å的面心立方格子. 在同素异形变化中观察到一个有趣的事实:甚至在晶格改变时,原子间距d保持不变. 原子间距似乎是所考虑的特殊原子固有的特性. 于是可以合理地认为,晶体中的原子是相互接触着的球体. 球的半径就是原子半径,应该等于
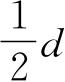 . 所以金属铁的原子半径是1.29Å,而金属钴的原子半径是1.26Å. 图1.5是金属原子的原子半径r与原子序数Z的关系曲线. 这里周期变化是很明显的,并且与化学性质的周期变化相一致. 碱金属的半径最大,其次是碱土金属,过渡金属有较小的半径.
. 所以金属铁的原子半径是1.29Å,而金属钴的原子半径是1.26Å. 图1.5是金属原子的原子半径r与原子序数Z的关系曲线. 这里周期变化是很明显的,并且与化学性质的周期变化相一致. 碱金属的半径最大,其次是碱土金属,过渡金属有较小的半径.
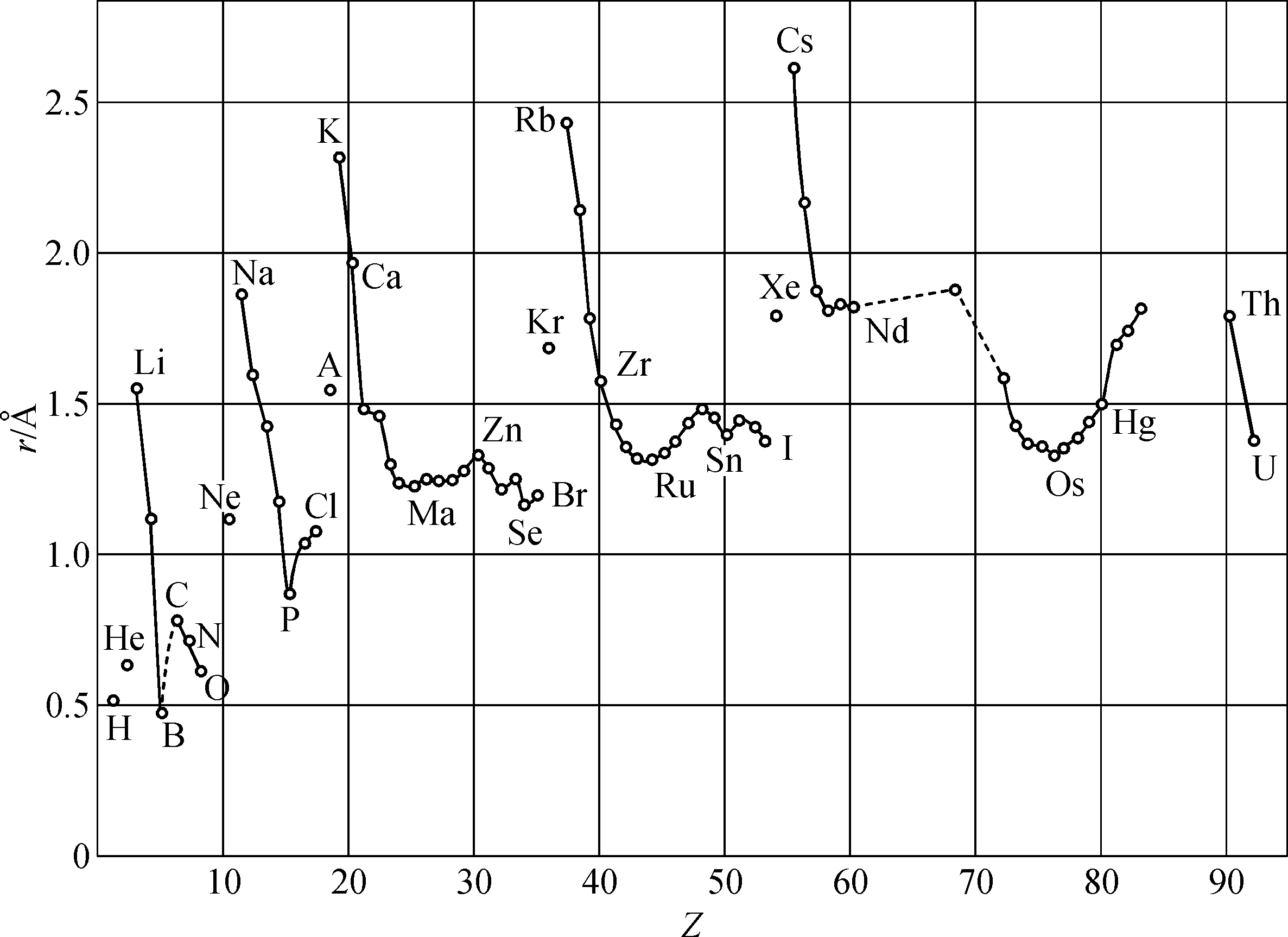
图1.5 原子半径r与原子序数Z关系曲线
同理,可以推广到离子晶体,只是晶格点座现在被离子(非原子)占据了. 表1.4给出离子的晶体半径值,这是泡令(L. Pauling)
 计算并编纂的. 我们看到,金属元素的离子比对应的金属原子小得多. 这自然是可以预料的,因为形成离子时要由原子剥夺价电子. 根据同一理由,我们预料正离子比同一元素的负离子小得多,这在表1.4中已证实了. 根据这个表,在NaCl晶体中,原子间距是0.95+1.81=2.76Å,这与图1.4所表示的测量值2.81埃差别不很大,并且更仔细地考虑晶体的几何情况后可以解释这一差异.
计算并编纂的. 我们看到,金属元素的离子比对应的金属原子小得多. 这自然是可以预料的,因为形成离子时要由原子剥夺价电子. 根据同一理由,我们预料正离子比同一元素的负离子小得多,这在表1.4中已证实了. 根据这个表,在NaCl晶体中,原子间距是0.95+1.81=2.76Å,这与图1.4所表示的测量值2.81埃差别不很大,并且更仔细地考虑晶体的几何情况后可以解释这一差异.
表1.4 离子的晶体半径 (单位为Å)
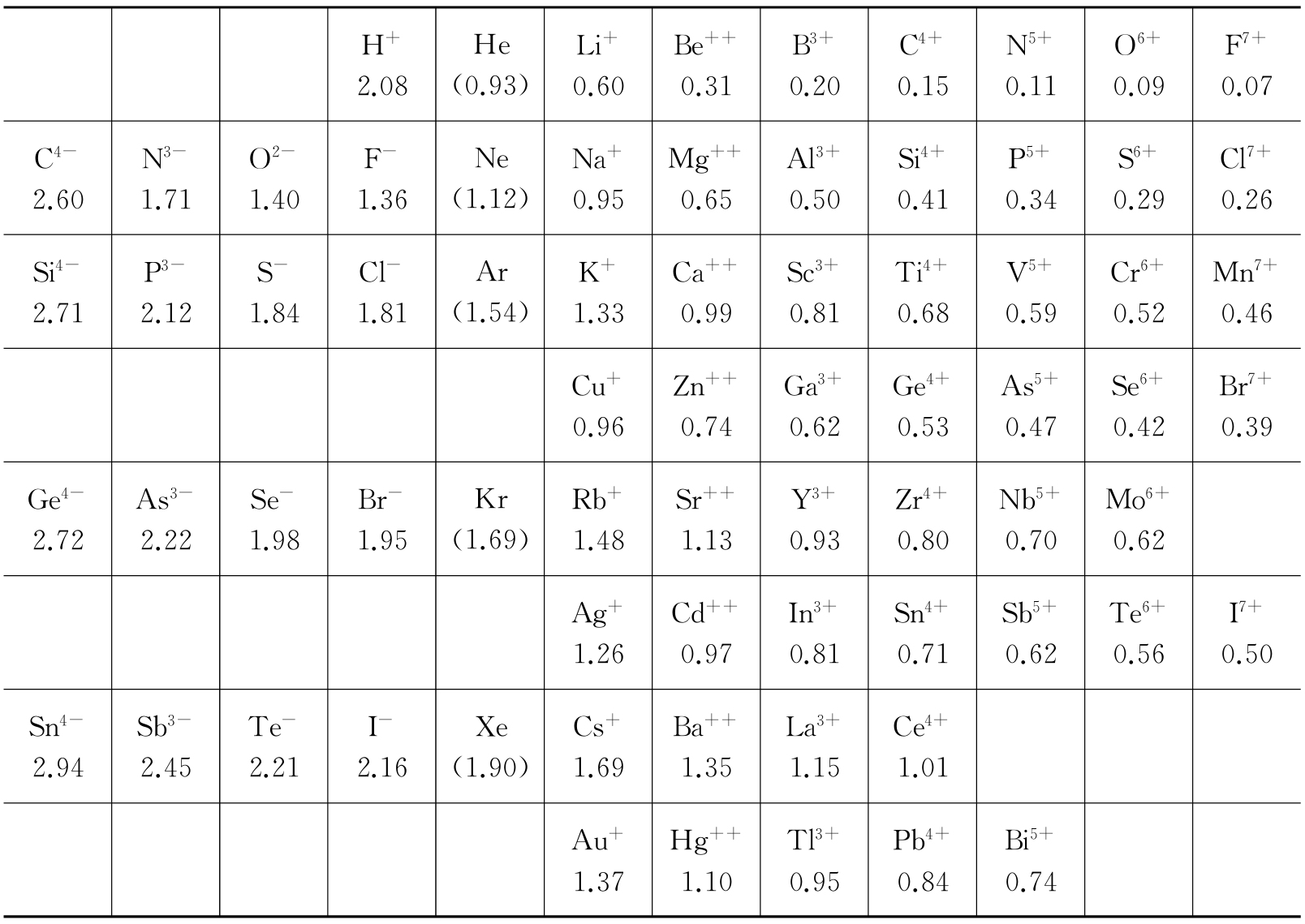
图1.1~1.4不符合上面所说的原子和离子半径的概念——原子与离子应该画得更大些. 体心立方格子和面心立方格子应该分别像图1.6和1.7那样表示. 在这些图中,原子是相互接触着的,半径是原子间距的一半. 这种标准的或者平均的原子间距的概念也可以应用到分子结构中去. 我们自然应当认识到,原子间距依赖于原子间的相互作用或者键的类型. 我们已经看到,由于金属键与离子键的差异给出两组半径. 在很多分子中,共价键是最重要的键型,它有着自己的一组半径. 表1.5就是由泡令所编纂的一组. 在共价键中,原子间距是成键原子的共价半径的和. 例如碘甲烷中碳原子和碘原子间的距离是碳和碘原子的单键共价半径的和,或0.771+1.33=2.10Å. 测量值是(2.10±0.03)Å. 同一化合物中碳和氢原子间的距离是0.773+0.30=1.07Å. 测量值是1.09Å.
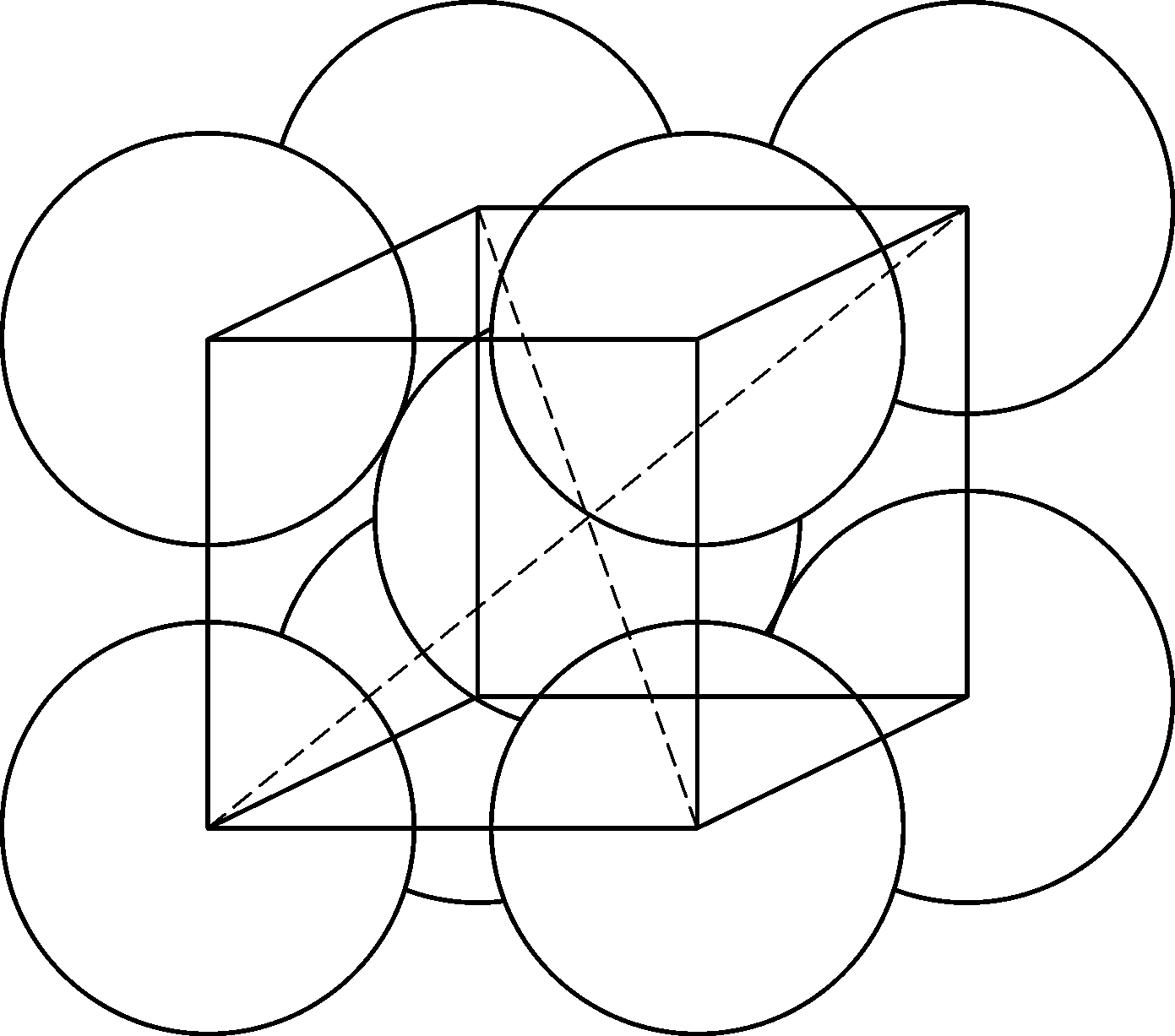
图1.6 体心立方晶格的原子半径
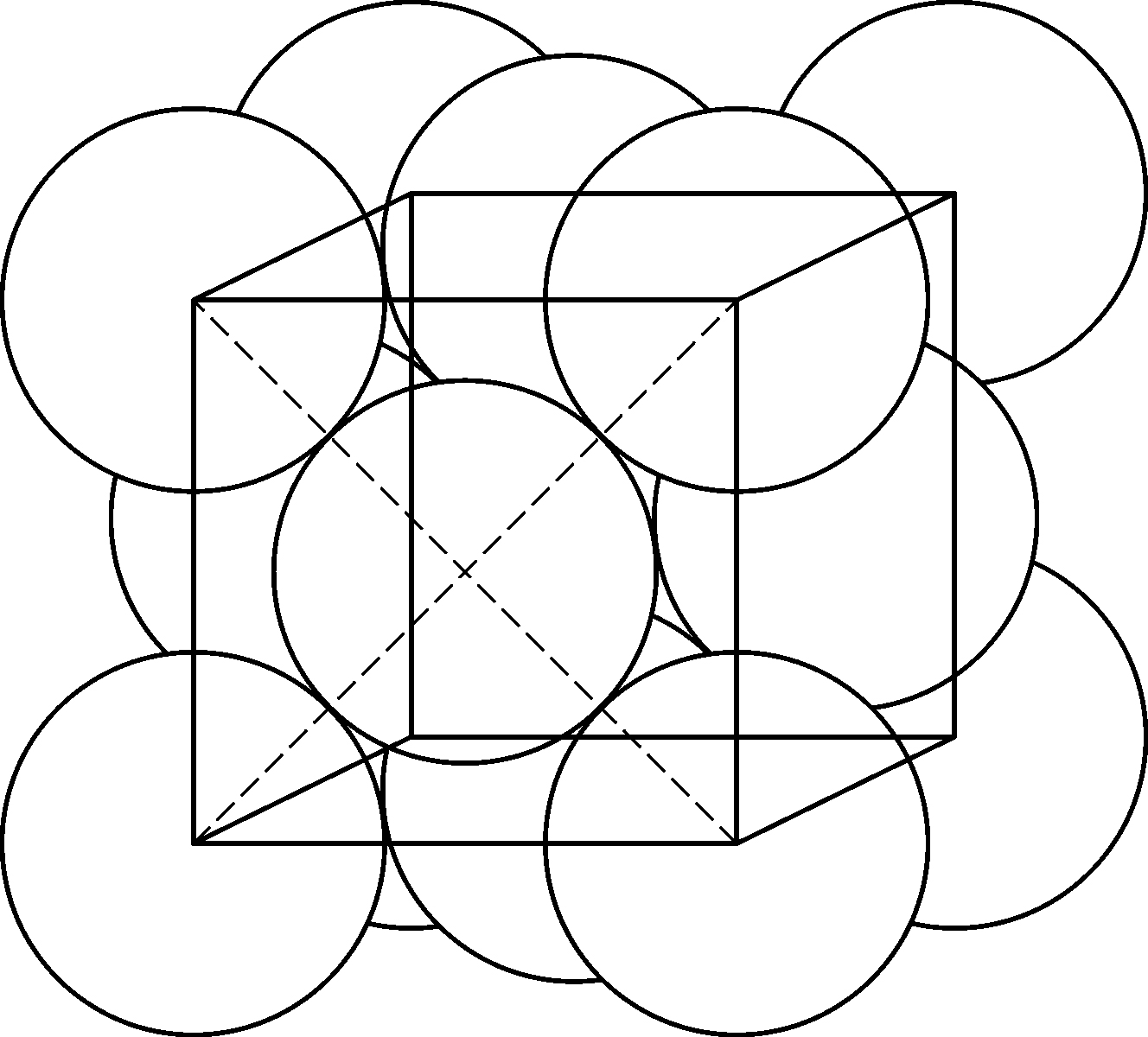
图1.7 面心立方晶格的原子半径
表1.5 原子的共价半径 (单位为Å)
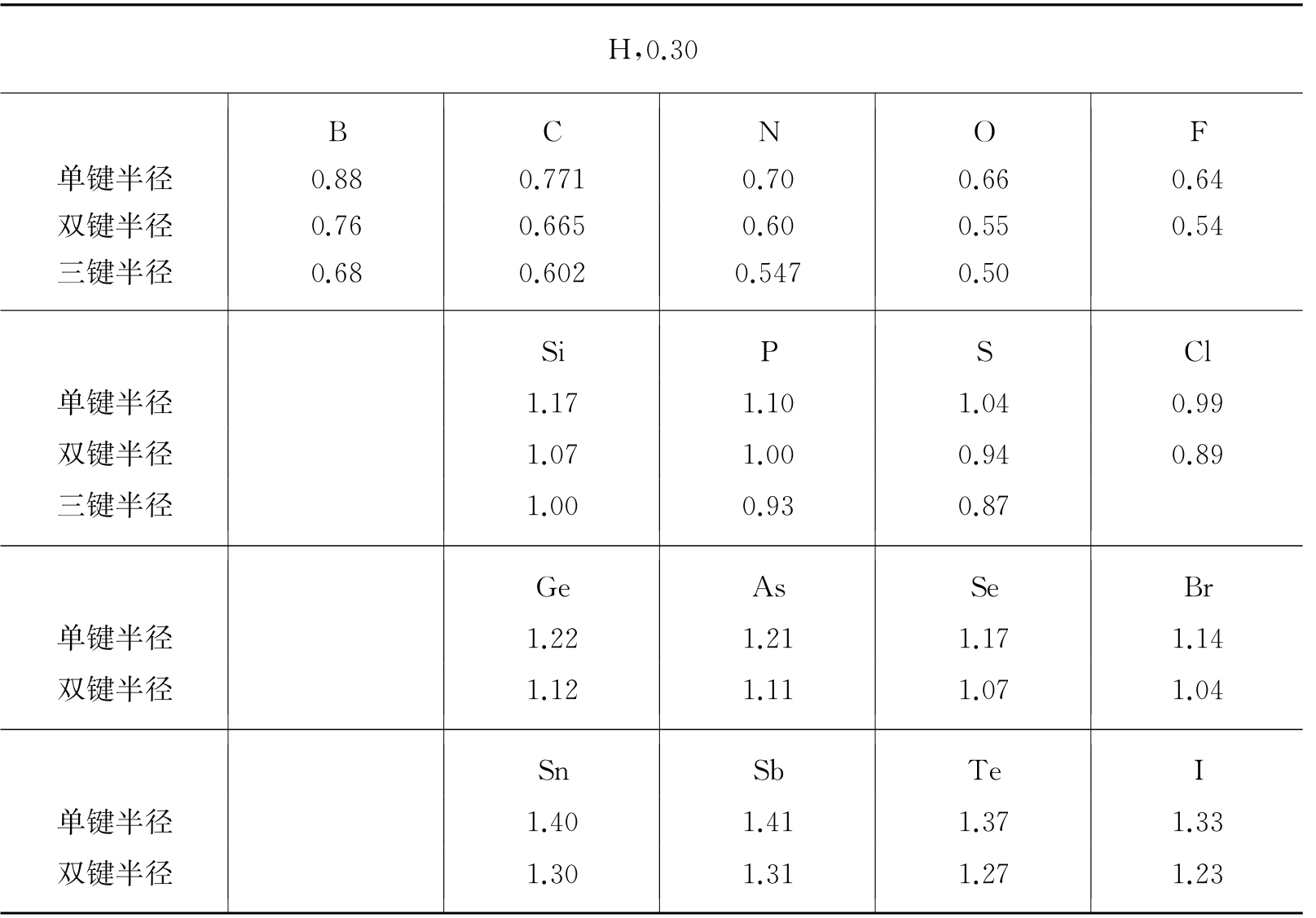
利用表1.5中的共价半径,如果我们还知道键的方向,即键角,就很容易搭起分子的空间架子. 以碘甲烷分子来说,关键是碳原子. 理论和实验结果指出:以四个单键和其他原子相结合的碳原子,其四个键近似地指向正四面体的四角,而本身则位于中心. 两两键之间的夹角近于109°28′(四面体的中心角). 金刚石的晶体结构就有这一键角值. 其他原子的键角列在表1.6中,这也是泡令编纂的. 硅也有正四面体的键角.
表1.6 键角的实验值
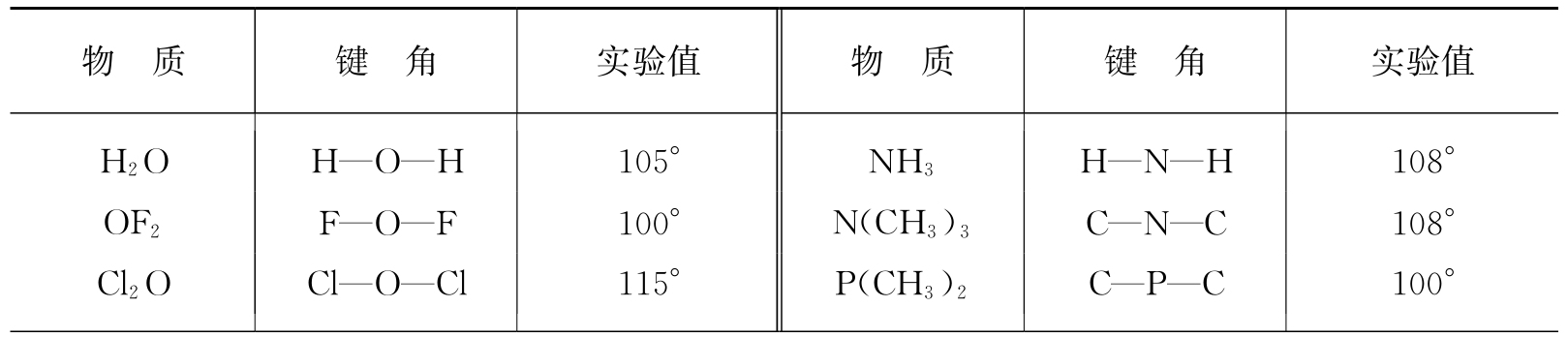
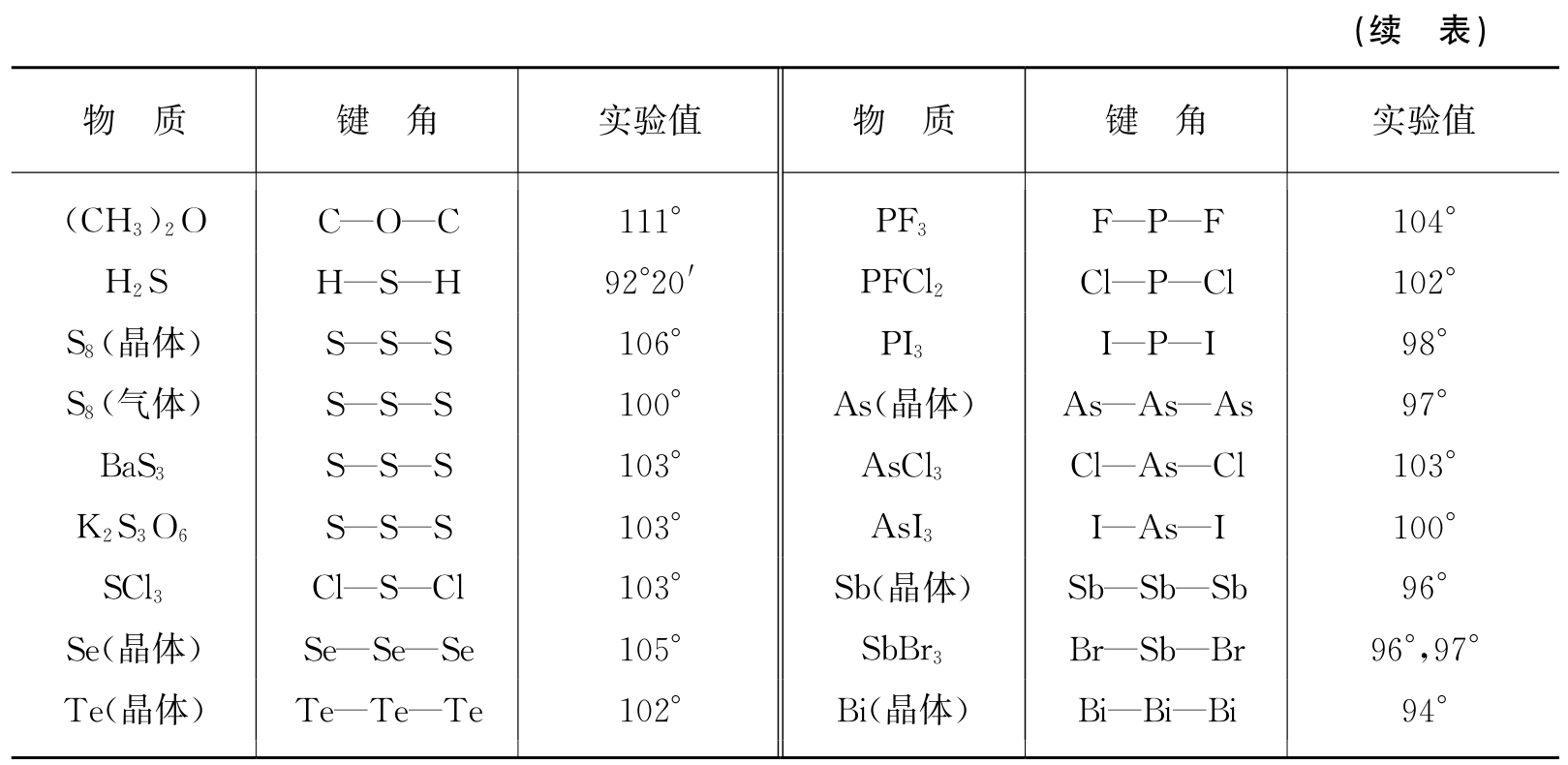
为了确定分子的形状,除了分子中原子的排列以外,我们还需要知道原子和分子的电子云有效边界. 当另一分子的电子云穿入这一边界时,分子之间就产生排斥力. 由于分子间力又叫范德瓦耳斯(van der Waals)力,往往把这一有效边界的半径叫作范德瓦耳斯半径. 我们从分子骨架中的每一个原子中心以相应的范德瓦耳斯半径作圆球,就可以确定分子的形状. 图1.8就是这样画成的几个简单分子. 在表1.7中列举了一些原子的范德瓦耳斯半径,这也是泡令所给出的.
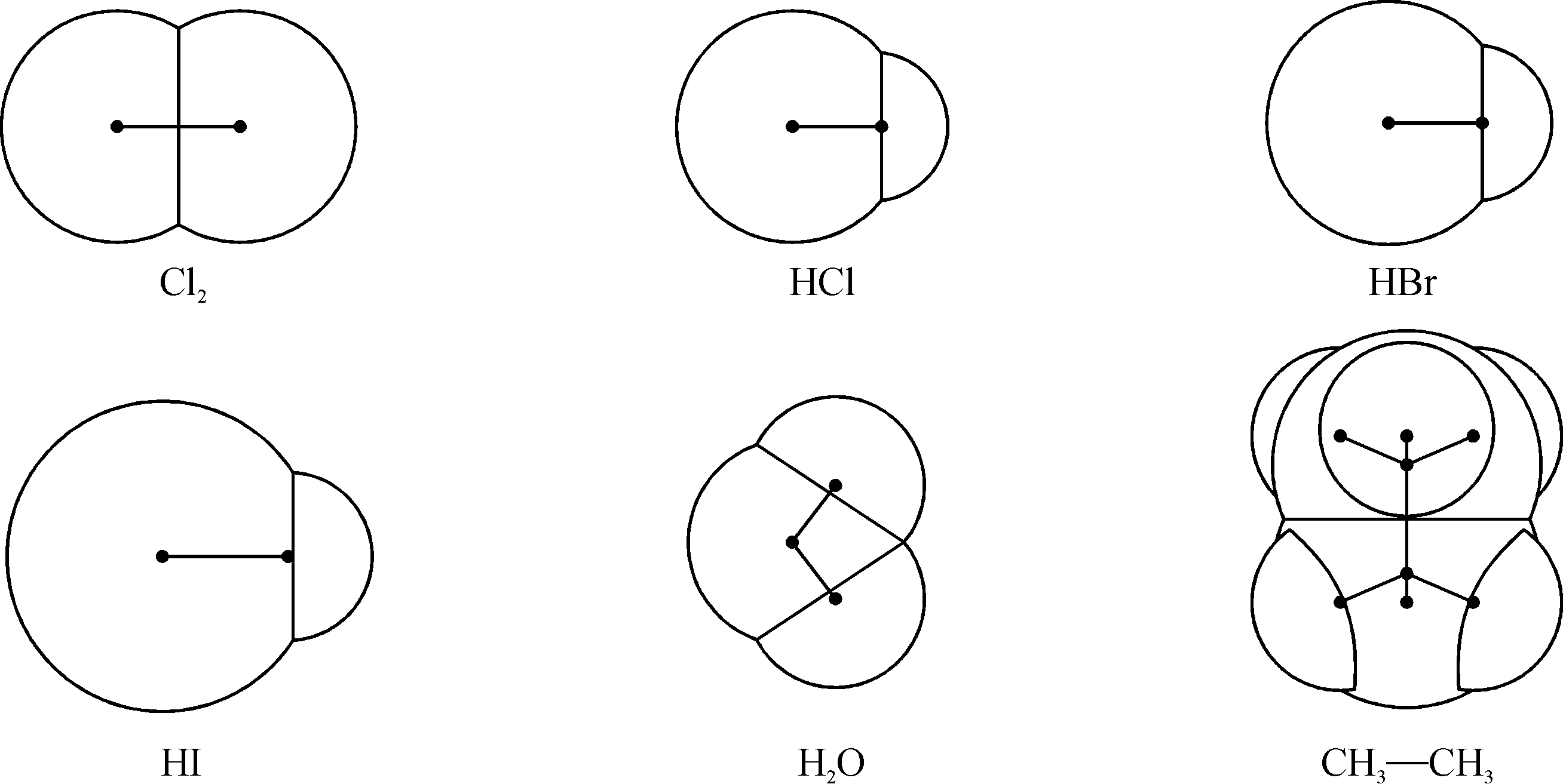
图1.8 常见简单分子的形状
表1.7 原子的范德瓦耳斯半径 (单位为Å)


甲基,CH 3 ,2.0Å.
芳香族分子的厚度,1.85Å.