




对于第二类系集,如果它的配容一定要用4.3节中所述的方法计算,那么,系集平衡态的计算就需要采用新的方法. 为了简单起见,如果所考虑的系集包含两组非定域系A和B,其数目各为N A 和N B ,体系A和B各有一系列的状态,我们先假设它们都是非退化的,其能量各为ε 0 ,ε 1 ,…,ε r ,…和η 0 ,η 1 ,…,η s ,…,而且均可表为适当能量单位的整数倍. 在这些状态上,体系的数目仍用n 0 ,n 1 ,…,n r ,…及n' 0 ,n' 1 ,…,n' s ,…表示. 此组数目完全地代表了系集的一个统计状态. 现在系集的本征函数对于给定的一组体系中的各个体系是对称的或者是反对称的,这两种情形必须区别对待.
(i)系集的本征函数对给定的一组体系是对称的. 我们说,这种体系所组成的系集遵守玻色-爱因斯坦(Bose-Einstein)统计.
由4.3节可知,对于n r 、n' s 的每一组正整数(或零)值,只有一个本征函数与之对应. 因此,总配容数C等于能满足于必要等式
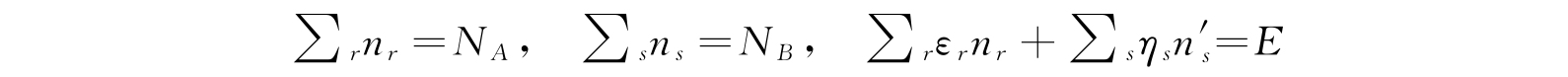
的n r 、n' s 正整数(或零)的组数. 现在我们将指出:双连乘积
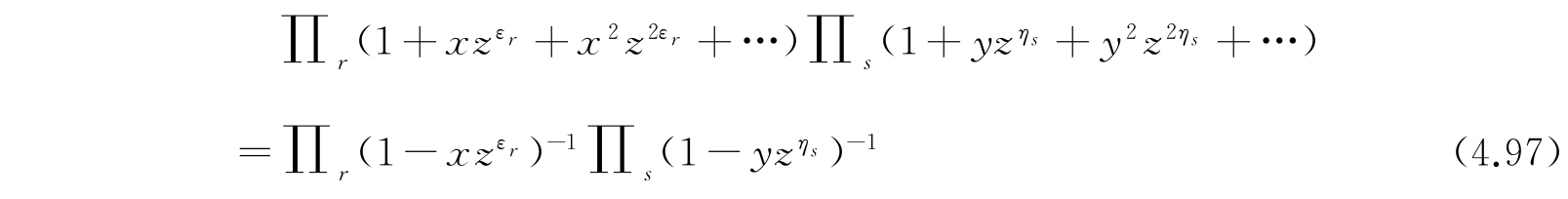
对x、y、z作幂级数展开,展开式中的
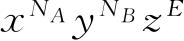 项的系数就是C. 考虑展开式中与体系A的第r个状态相应的因子. 为此,在作乘积时,我们必须选取形式为
项的系数就是C. 考虑展开式中与体系A的第r个状态相应的因子. 为此,在作乘积时,我们必须选取形式为
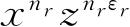 的一项. 乘积∏
r
( )的展开式的代表项是
的一项. 乘积∏
r
( )的展开式的代表项是
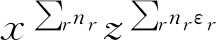 ,其中n
r
可以取任何正整数(或零). 另一乘积∏
s
( )的展开式的代表项是
,其中n
r
可以取任何正整数(或零). 另一乘积∏
s
( )的展开式的代表项是
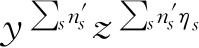 ,n'
s
可取任何正整数(或零). 因此,全部表示式的展开式的普遍项是
,n'
s
可取任何正整数(或零). 因此,全部表示式的展开式的普遍项是
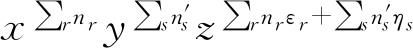 ,其中n
r
、n'
s
可独立地取任何正整数(或零). 假如我们在展开式中选取
,其中n
r
、n'
s
可独立地取任何正整数(或零). 假如我们在展开式中选取
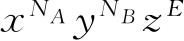 项,那么,n
r
、n'
s
恰好只能取满足于必要等式的那些值,因此这一项的系数是C.
项,那么,n
r
、n'
s
恰好只能取满足于必要等式的那些值,因此这一项的系数是C.
可以看到,x和y所起的作用与z所起的作用是相似的. 变量x选取满足于给出正确N A 值这一配容限制条件的那些项,变量y选取满足于给出正确N B 值这一条件的那些项. 这种限制条件对于定域系是被自动满足的. 变量z与对于定域系一样,选取满足于给出正确E值的那些项.
在式(4.97)中我们感兴趣的一项是
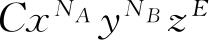 ,我们把这一项看作是C个相等的项
,我们把这一项看作是C个相等的项
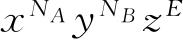 之和,每一项对应一个配容. 考虑其中的某一个配容,如果在这个配容中能量为ε
t
的A体系共有n
t
个,那么,这个配容所对应的那一项
之和,每一项对应一个配容. 考虑其中的某一个配容,如果在这个配容中能量为ε
t
的A体系共有n
t
个,那么,这个配容所对应的那一项
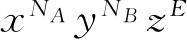 中包含因子
中包含因子
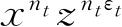 ;而且下标t的因子也只有这一个. 如果我们用
;而且下标t的因子也只有这一个. 如果我们用
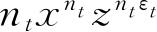 代替因子
代替因子
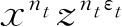 ,并且对于其他的配容也作同样的代替,那么,
,并且对于其他的配容也作同样的代替,那么,
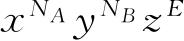 的系数就由∑
1
变为
的系数就由∑
1
变为
 了;此处求和号是对C个配容求和. 由式(4.1)可知,这样做就相当于把
了;此处求和号是对C个配容求和. 由式(4.1)可知,这样做就相当于把
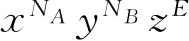 的系数由C变成
的系数由C变成
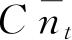 . 我们知道,
. 我们知道,
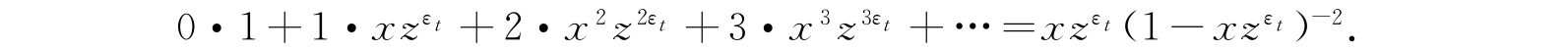
因此,如果在式(4.97)中我们用
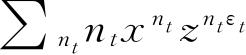 代替
代替
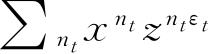 ,或者说,用
,或者说,用
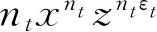 代替各个
代替各个
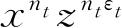 ,就得到
,就得到
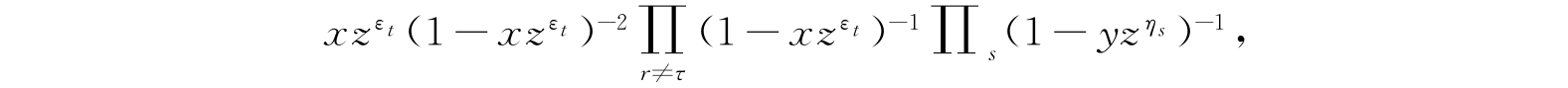
或者写为
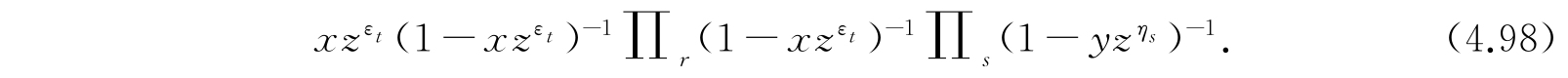
由以上所述可知,
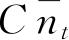 正好是式(4.98)的展开式中
正好是式(4.98)的展开式中
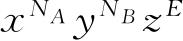 项的系数.
项的系数.
(ii)系集的本征函数对给定的一组体系是反对称的. 我们说,这样的体系组成的系集遵守费米-狄拉克(Fermi-Dirac)统计.
对于这种系集,对应于n r 、n' s 的每一组被允许的值,仍然是只有一个本征函数,但n r 、n' s 的值仅可以取0或1,因为泡利不相容原理的限制不允许有大于1的值,因此,配容数C等于n r 、n' s 值的组数,而n r 、n' s 必须满足式(4.39)、(4.40)及(4.41)并且只可能是0或1. 与对于玻色-爱因斯坦统计中所作的说明同样道理,可以指出配容数C等于双连乘积
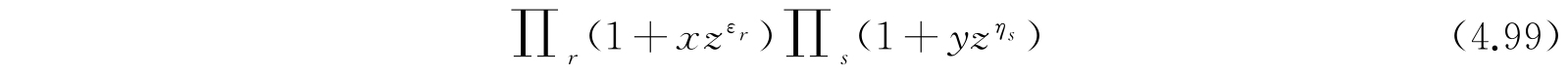
的展开式中
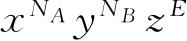 项的系数. 同样,我们将式(4.99)中具有下标t的项
项的系数. 同样,我们将式(4.99)中具有下标t的项
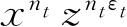 用
用
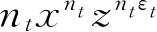 代替,那么,它的展开式中
代替,那么,它的展开式中
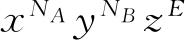 的系数就是
的系数就是
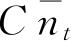 . 只不过现在n
t
只可能是0或1. 因此,式(4.99)中的下标t的因子
. 只不过现在n
t
只可能是0或1. 因此,式(4.99)中的下标t的因子
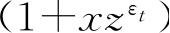 现在应当用
现在应当用
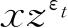 代替. 这就相当于用
代替. 这就相当于用
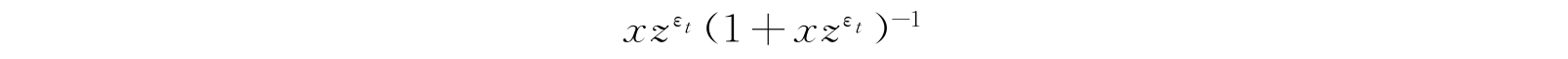
去乘式(4.99). 因此,我们看到,在
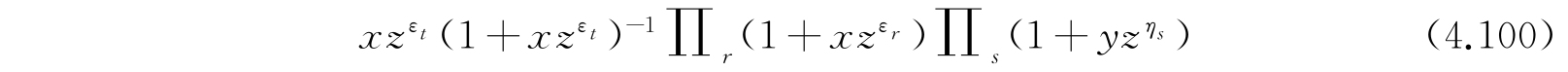
的展开式中,
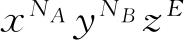 的系数就是
的系数就是
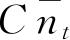 .
.
我们注意到,对于玻色-爱因斯坦统计的式(4.97)、(4.98)与对于费米-狄拉克统计的式(4.99)、(4.100),两者只有符号上的差别. 因此,我们可以将两种统计的公式合并在一个共同的形式下进行讨论,同时我们也容许系集中的两组体系可以遵守不同的统计法. 这样,我们得到一个有普遍意义的结果,即配容数C等于在
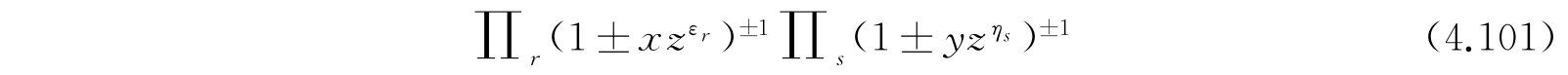
的展开式中
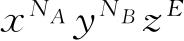 的系数. 在这里,在第一个乘积号下取“+”或者“-”要视体系A是否遵守玻色-爱因斯坦统计或是费米-狄拉克统计而定,同样,在第二个乘积号下的符号的选取要视体系B的性质而定. 另一个结果是,如果体系A处于状态t的平均数目是
的系数. 在这里,在第一个乘积号下取“+”或者“-”要视体系A是否遵守玻色-爱因斯坦统计或是费米-狄拉克统计而定,同样,在第二个乘积号下的符号的选取要视体系B的性质而定. 另一个结果是,如果体系A处于状态t的平均数目是
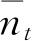 ,那么,
,那么,
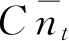 等于在
等于在
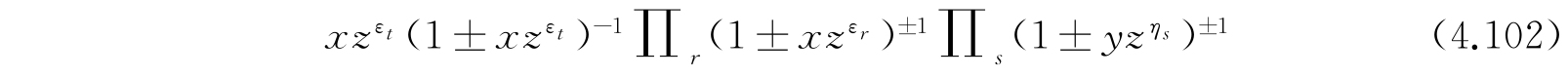
的展开式中的
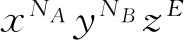 项的系数.
项的系数.
在下节里,我们将处理计算这些系数的纯数学问题.