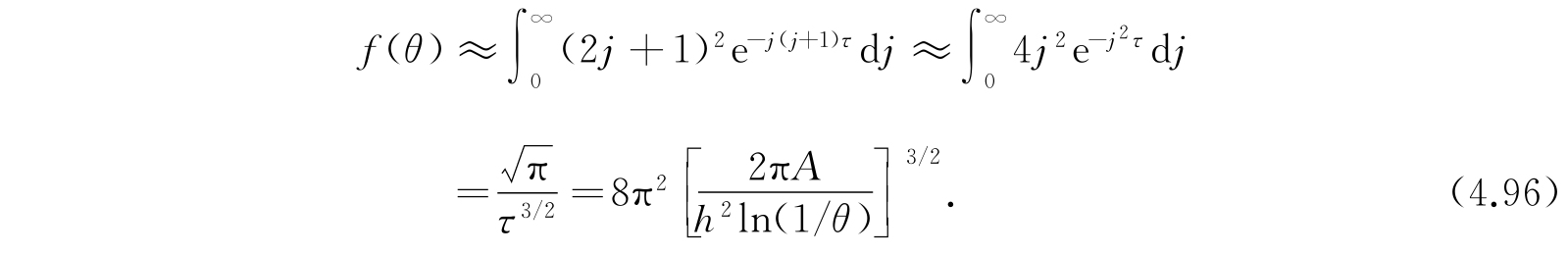下载掌阅APP,畅读海量书库
立即打开




设A是横向转动惯量,C是轴向转动惯量,它的能量的可能值在2.17节中已给出,它们是
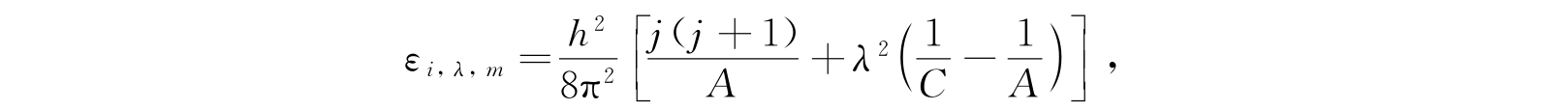
此处
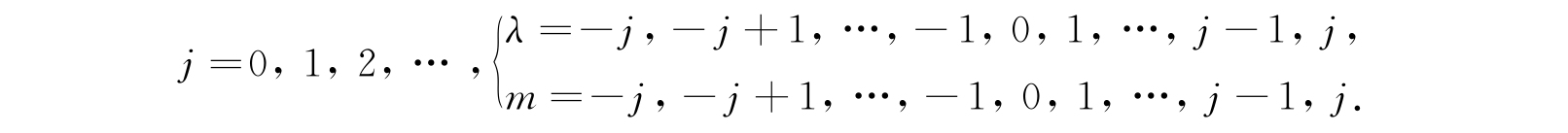
因为体系有三个自由度,故有三个量子数j、λ、m,但是由于空间退化,事实上只需要其中的两个量子数j及λ就完全决定了能量值. 因此,我们可将ε i,λ,m 中的下标m略去而将这具有不同m值的2j+1个状态归结成一个权重为2j+1的退化状态. 如此则配分函数为
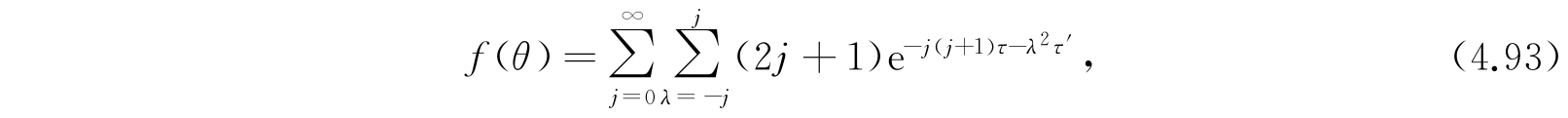
此处
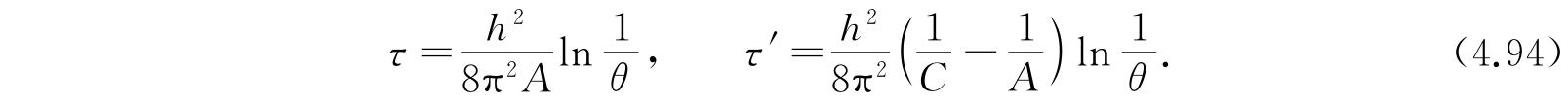
如果不采用近似方法,式(4.93)不能够化简. 但是在具体应用上,我们常常遇到τ≪1,τ′≪1的情况. 那么,可应用积分代替求和,而又用分部积分得到近似式如下:
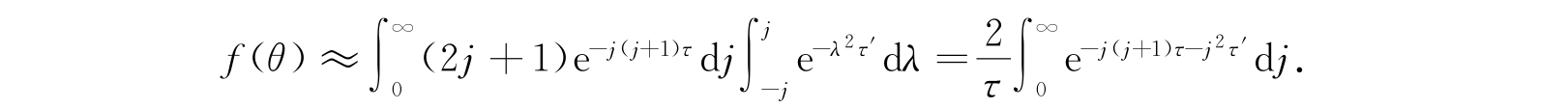
因为τ和τ′很小,所以积分的主要贡献来自j的一段很长的区间,也就是j比较大,这样,使得在被积函数敏感的区间中较大的一段里,j(j+1)可以用j 2 代替. 故上式可近似写为
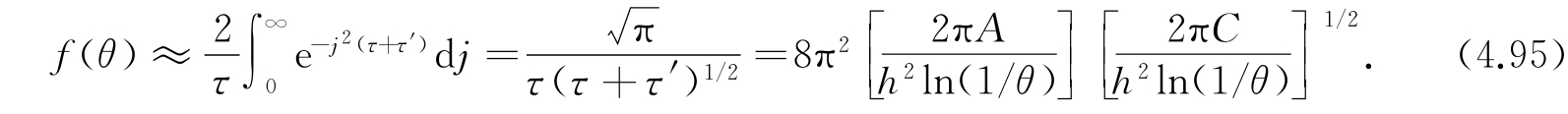
对于完全对称的转动体,C=A,因而τ′等于零. 此时能量不但与m无关,而且也与λ无关,故退化程度增加了. 在此情形下,
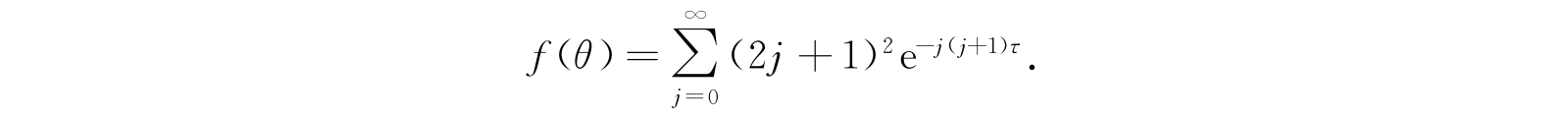
当τ≪1时,我们可以用积分代替求和而得到近似公式