下载掌阅APP，畅读海量书库
立即打开
在4.2节以及在第2章中曾经指出，没有轴自旋的刚性转子的能级
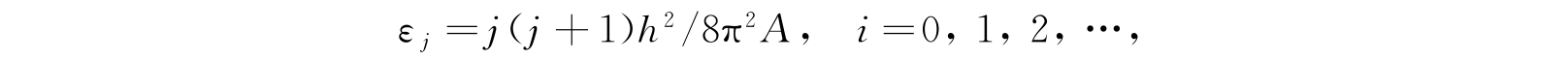
其中A是横向转动惯量. 状态j的权重是（2j+1）. 因此配分函数
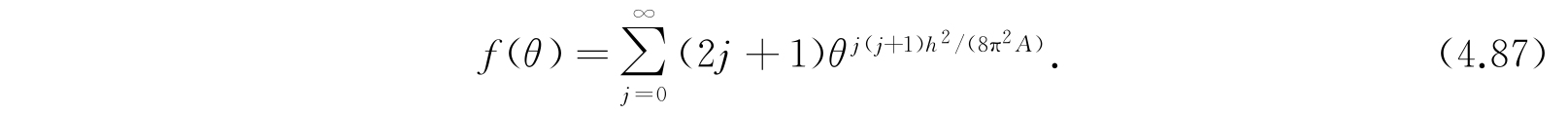
作代换，
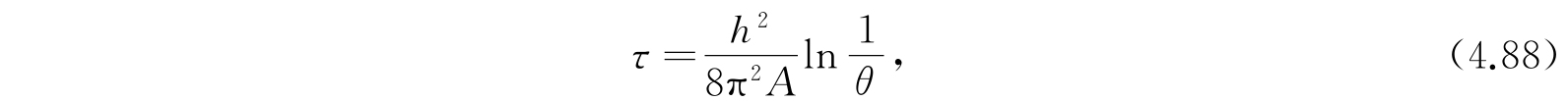
则
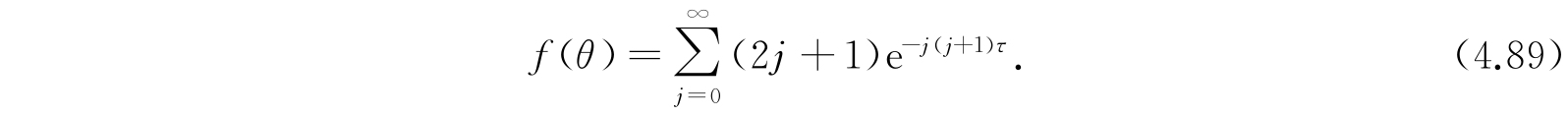
首先，我们对于τ≪1的情形作近似计算（这是常遇到的情形）. 由于τ≪1，故指数因子随j值的变化很慢，因而求和可以用积分近似. 利用变换
j（j+1）τ=ξ，（2j+1）τdj=dξ，
我们得
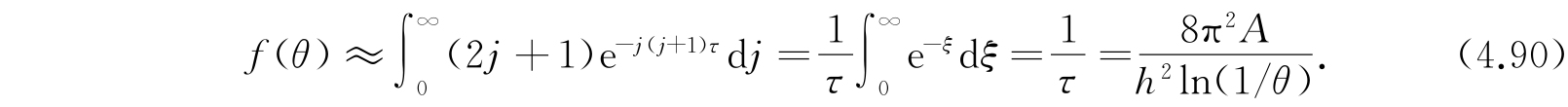
如果要得到更准确的配分函数的计算，我们可以用欧拉-麦克劳林展开式. 欧拉-麦克劳林展开式表述如下：设F（x）对a≤x≤rω中所有的x值是解析的，于是
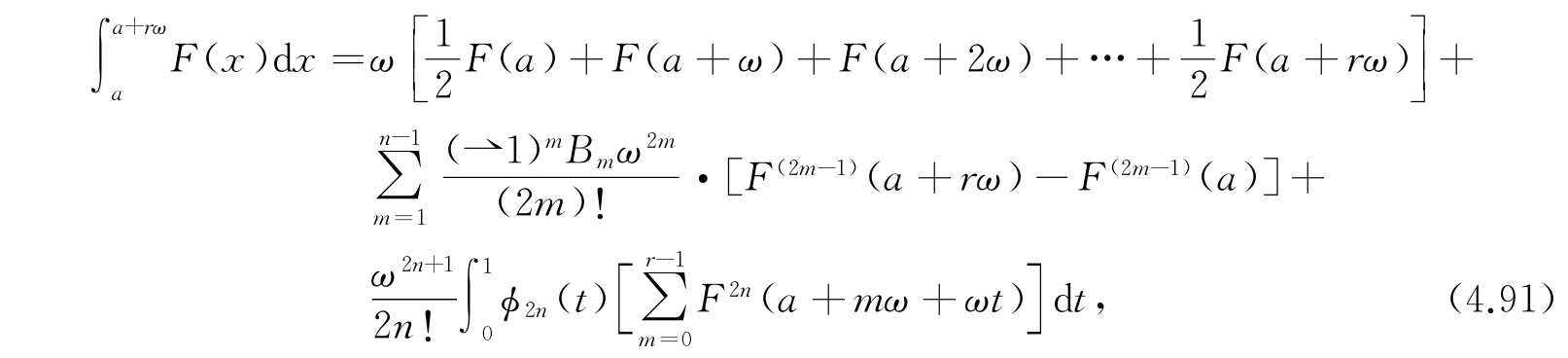
其中B m 是第m个伯努利（Bernoulli）数，ϕ 2n （t）是2n级的伯努利多项式. 将这个展开式应用于式（4.89），现在
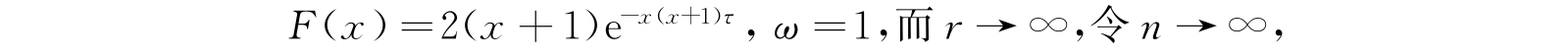
那么，
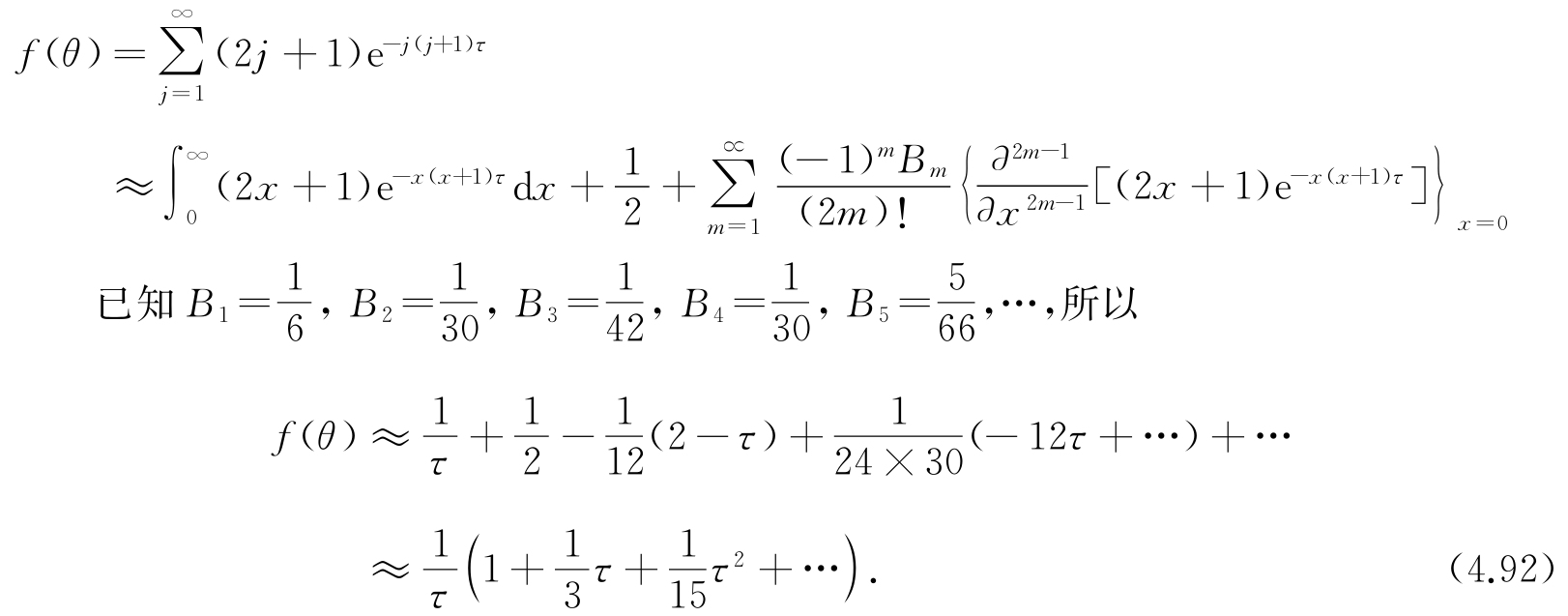
这个结果首先由缪尔霍兰（Mulholland）
用了很复杂的分析而得到的；他的辛勤计算确立了这个展开式的渐近性质，我们的计算虽然简单，但没有证明这一点. 在第5章中讨论双原子分子时还要用到这一公式.