下载掌阅APP，畅读海量书库
立即打开
我们先考虑一个二维各向异性谐振子，这就是说，在两相互垂直的方向上振子振动的自然频率不同. 取势能的极小点为原点及振子的主轴x和y，这样，经典能量方程为
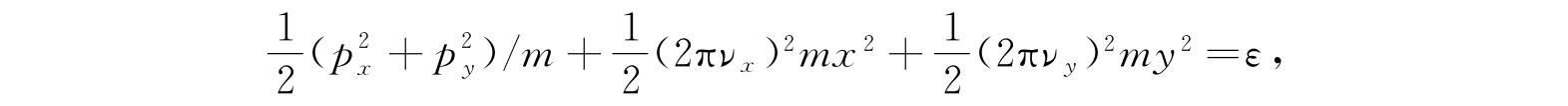
其中p x 、p y 是沿x、y轴的动量，ν x 、ν y 是各与沿两个主轴的回复力常数有关的频率，ε是能量，它以原点能量为零. 对应的薛定谔方程为
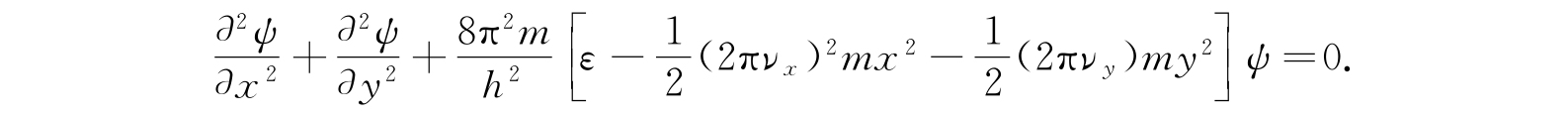
分离方程的自变量，得到自变量为x及y的方程，这两个方程恰好是具有频率为ν x 及ν y 的线性谐振子方程. 因此，能级的形式为
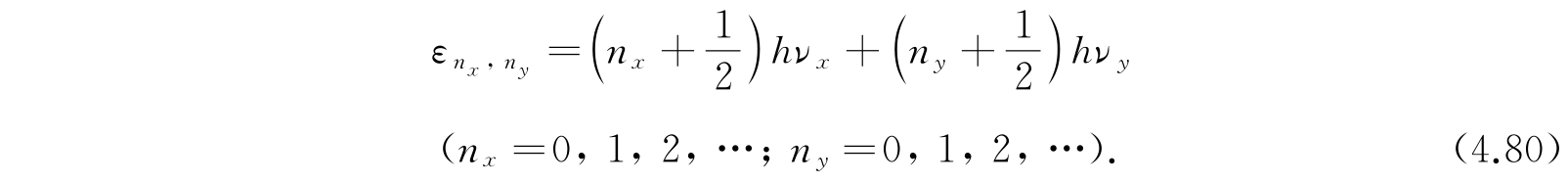
所以配分函数
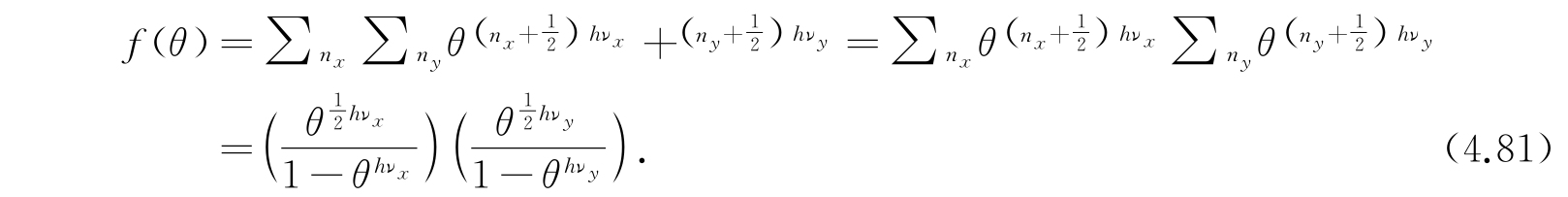
分布于N A 个这样体系上的平均能量
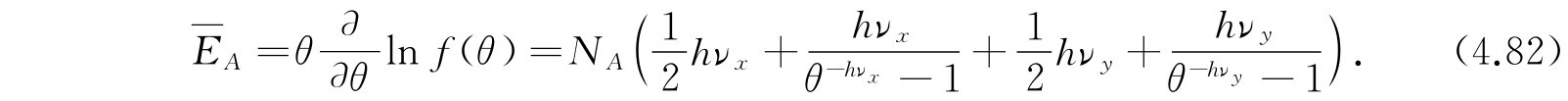
现在考虑二维各向同性谐振子，在4.2节中我们已经指出，它的能态是（n+1）hν，n=0，1，2，…，其权重为n+1. 因此，配分函数为
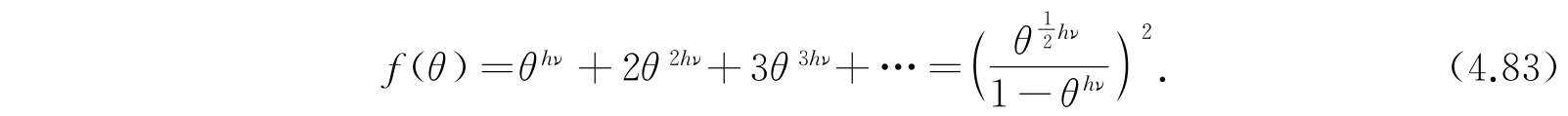
分布在N A 个体系的能量为
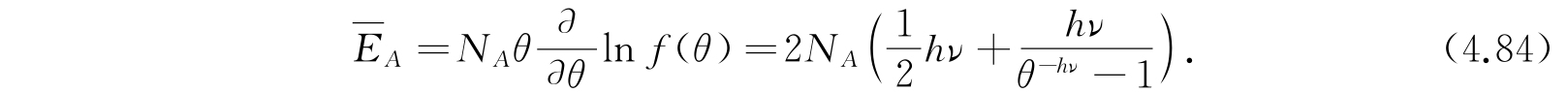
这些公式可以由式（4.81）及（4.82）中令ν x =ν y =ν而得到.
同样，对于三维各向同性谐振子可以证明能级是
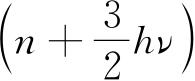，n=0，1，2，…，其权重为
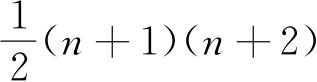. 所以配分函数为
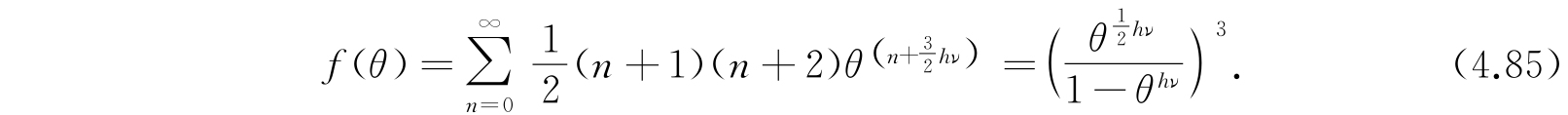
N A 个体系的平均能量
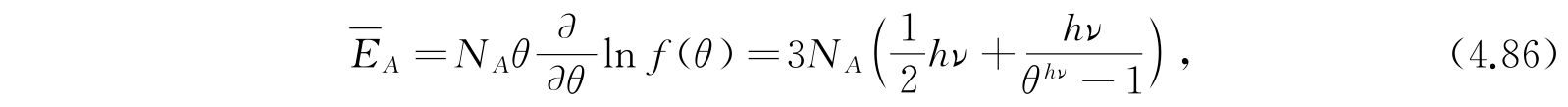
正如我们所想象的，它恰好是线性谐振子平均能量的三倍.