下载掌阅APP，畅读海量书库
立即打开
到现在，我们已经讨论了定域线性振子系集的平均性质，在讨论中，我们只假定了这些振子有一系列由一个量子数所决定的不连续状态，而这些状态之间没有具有相同能量的状态，除此之外，我们并没有对这些振子作任何假定. 因此，所得到的公式可以用于任何单自由度体系. 实际上，主要的单自由度体系只有线性振子. 一般实际问题中所遇到的多半都是多自由度体系. 但是在以上的探讨中，体系状态为一个量子数所决定的这一要求，我们从来也没有引用，我们要求的只是每一个量子数对应一个能量；因此，设有一自由度是p个的体系，如果我们认为状态r是由量子数r
1
，r
2
，…，r
p
所决定的，设状态的能量
彼此不同，则以上的公式仍可以直接过渡成多自由度体系的.
现在我们要去掉没有两个状态的能量相等这一假设，进一步把我们的公式推广到退化体系. 设有
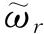个状态有相同的能量ε
r
. 我们把这些状态归为一组，称之为
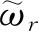重退化的单个状态或称权重为
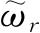的状态. 如果我们将体系所受的约束给以适当的小改变，例如将外力场以小改变（给以微扰）. 一般说这
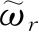个能级可能分裂开来，这时体系就成为非退化的了. 于是以前的公式都可以直接应用，而
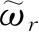个被分裂了的能级每一个都对应于配分函数
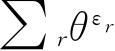中的一项. 我们再使微扰趋于零，则体系又回到原来的情形，
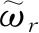个状态又有了同样的能量ε
r
. 现在配分函数
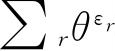包含
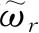个相等的项，故配分函数可以改写成
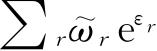，这里的求和是对各个退化状态的，或者说每个能级只加一次.
现在我们将结果重述一遍，同时现在的这些结果也是适合于退化体系的. 设系集包含N
A
个体系A、N
B
个体系B等. 设体系A具有一系列能量是ε
0
，ε
1
，…，ε
r
，…和权重是
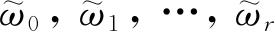，…的定态. 体系A的配分函数是
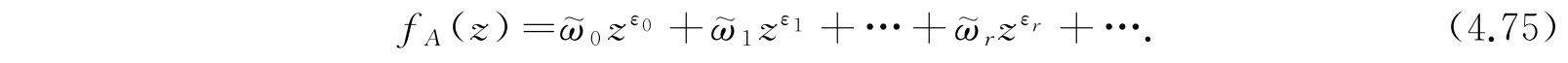
将式（4.67）推广于退化体系，则在能量为ε
r
的状态上，体系A的平均数目
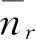可直接写成
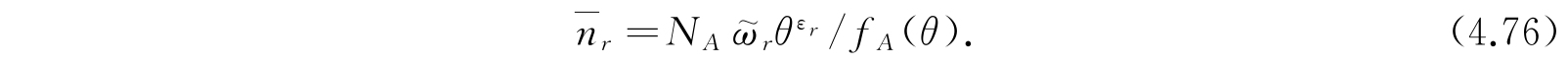
由式（4.67）可知，此退化状态上体系A的平均能量为
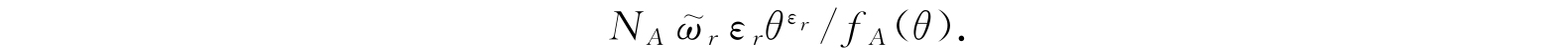
将上面的表示式对所有的状态r求和，则得体系A的平均能量
：
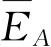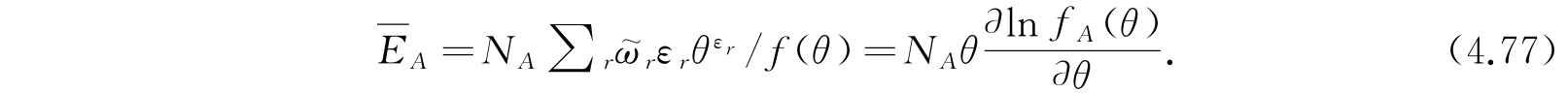
对于其他种体系有完全类似的公式，并且它们所用的θ都是一样的. 最后我们有必要的等式
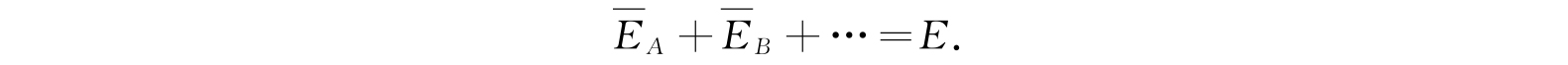
假如给出了E，便能决定统计温度θ. 反之，给出了温度θ，由公式可以决定E.
对于定域系我们定义有配分函数f（θ）. 必须注意到，对于多自由度体系，体系的运动常能够分成两个或多个相互无关的部分，在这种特殊情形下，配分函数是可以因式化的，其因子都是对应于某种运动的配分函数. 所谓体系运动分成几个相互无关的部分，是指在薛定谔方程的哈密顿量中，没有描述不同自由度的坐标的相乘积，所以，其本征能量是各个对应于不同自由度的，而由不同的量子数所决定的能量之和. 这样，由配分函数的定义可以直接看出，在这种情况下，配分函数可以因式化为几部分. 例如对于双原子分子，如果它的振动和转动的相互作用可忽略不计，则可以近似地把振动和转动分开，而将配分函数因式化为转动的和振动的两部分. 对于一个自由分子，它的内部运动和转动的确与分子的平移运动相互无关. 但是一般地说，只有气态系集中的体系才是自由分子，而气态系集的配容需要作为第二种类型计算.