下载掌阅APP，畅读海量书库
立即打开
现在我们把上一节的数学推导的结果以及这些推导所依据的4.4节的各公式再扼要地叙述一下. 并且我们也将把这些结论叙述得更为普遍一些，我们现在不限于只包含两种体系的系集.
考虑一个系集，它包含N
A
个体系A，N
B
个体系B，N
C
个体系C等，其中N
A
，N
B
，N
C
，…都是大数. 设体系A的可能状态为0，1，2，…，这些状态都是非退化的，其能量各为ε
0
，ε
1
，ε
2
，…，由上节的结果得知，体系A在能量为ε
r
的状态上的平均数目
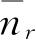是
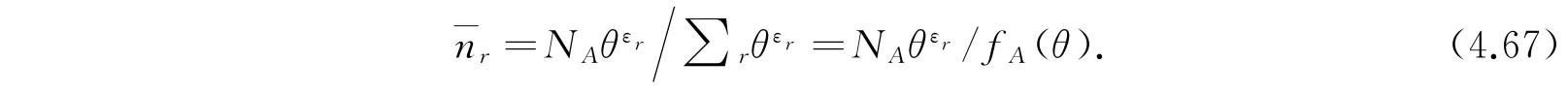
关于参数θ的意义，下面我们将讨论到. 同样，处于能量为η
s
的状态上，体系B的平均数
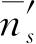是
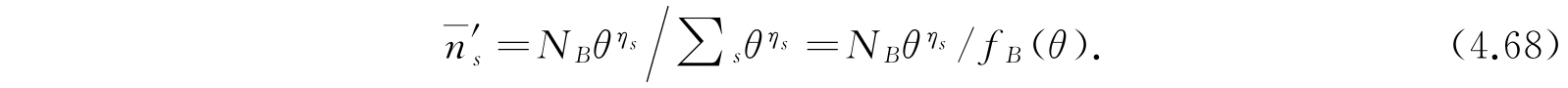
对于其他种体系亦有类似的公式. 由式（4.67）和（4.68）看到，方程
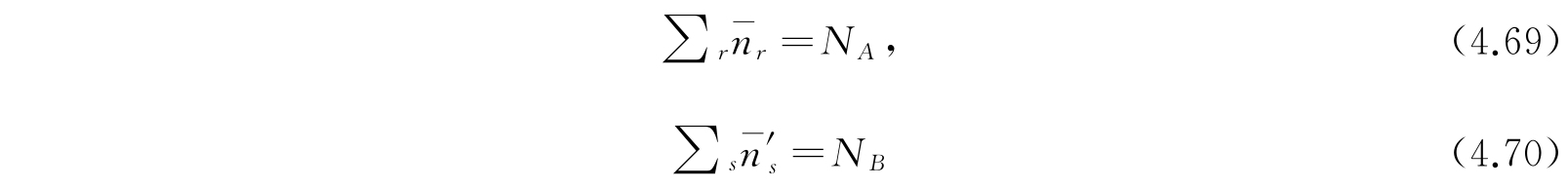
自动地被满足了.
能量在各种体系之间的平均分布如下. 全部体系A的平均能量是
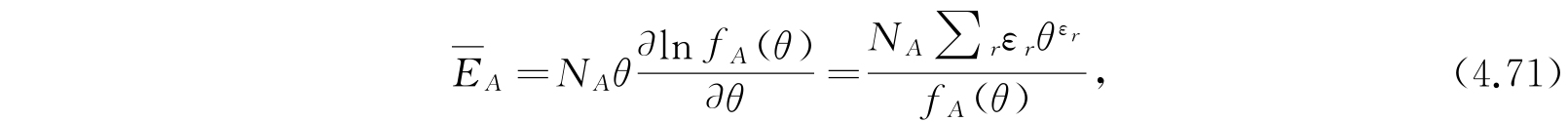
它满足实质方程
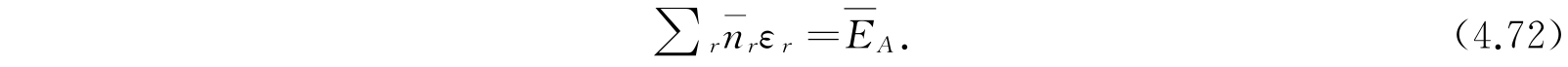
对于
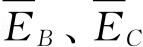等有类似的公式. 最后，我们有必要的等式
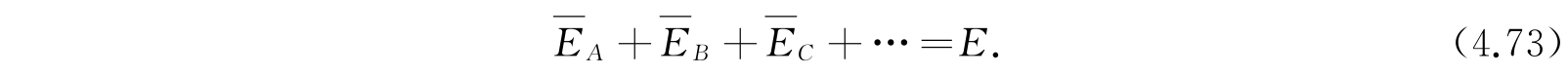
如果我们给出了E，则θ就确定了. 反之，若给出了θ，则E就确定了.
余下要讨论的是关于参数θ的意义. 很明显，在数学的本源上，θ是一个描写系集状态的基本参数，而且它应当与系集的某些物理性质有关. 参数θ的一个显著特点是，无论是体系A的平均性质，或是体系B的平均性质，或是体系C的平均性质等，都是由同一个θ决定的. 所以说，θ 是一个帮助我们确定系集状态的参数，它对系集中所有各组体系均有相同的值 . 这恰好是温度不同于其他参数的性质，所以我们必然会得出这样的结论，即θ是一个扮演温度角色的参数. 当然，它绝不会是用普通的温度标尺作度量，因此，我们称θ为统计温度，或称用统计温标测量的温度. 以后我们将推求出温度θ与常用的热力学温度T之间的关系. 我们事先指出，两种温度的关系为
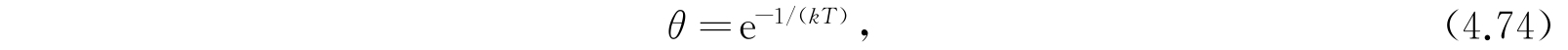
此处T是热力学温度（开尔文温标），k是普适常数.