4.5　最陡下降法的简单描述

由上一节知道，我们所要求的量是某些幂级数的某一项的系数. 利用柯西（Cauchy）定理，可以将它们表示为一些绕原点的复变量回路积分，

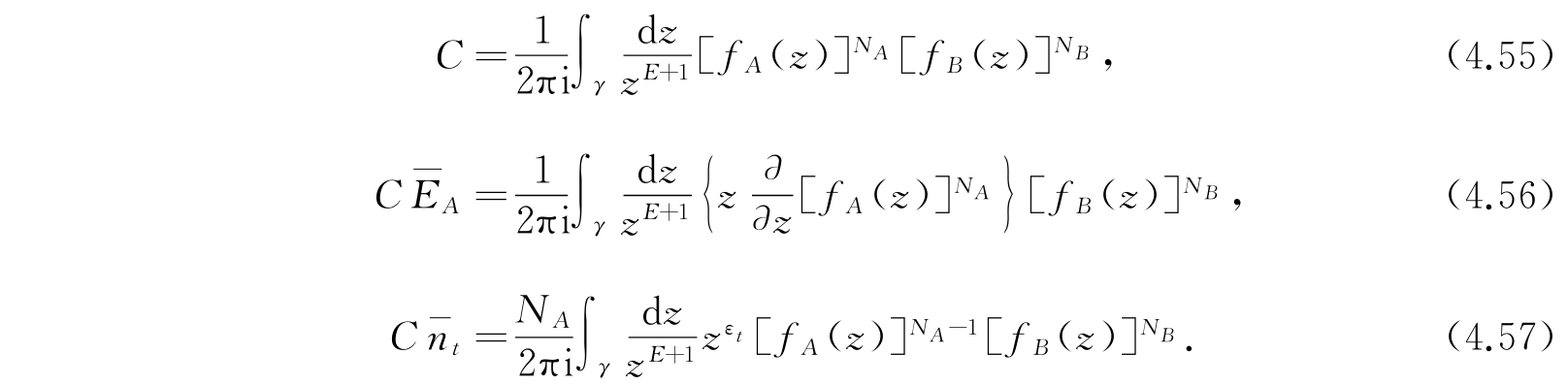
γ是幂级数收敛圆（实际上它的半径是1）中以逆时针方向绕原点一周的任意回路.

这些积分是严格成立的，对于N _A 、N _B 及E的任何值都成立. 但是只有当N _A 、N _B 及E很大的时候，在物理上才是有意义的，因为我们所能观测的系集都是包含有大量的体系. 因此我们先来求当N _A 、N _B 及E以固定的比例趋于无穷时积分的渐近值. 在物理上，这相当于我们将求的是当系集的内含性质不变而使系集的大小趋于无穷时系集的极限性质（所谓内含性质是指与系集的大小无关的性质）. 可以指出，一个有限系集的性质平常只能够从系集的极限性质推出. 这些积分的渐近值，在目前我们所考虑的这几个积分，以及更普遍的情形，都可以借助于最陡下降法把它严格地求出来.

考虑式（4.55）被积函数中乘在dz/z上的因子. 在正实轴上，这个因子在z→0及z→1时趋于无穷；在中间某一点z=θ，它取唯一的一个极小值. 将γ取以原点为心、θ为半径的圆，即z=θe ^iα ，于是当N _A 、N _B 及E值很大的时候，回路上此因子的模数在z=θ、α=0点是一个强极大值. 也就是由于被积式的微商在这一点等于零，所以对积分的全部贡献差不多都是来自这一点的附近. 假如被积函数中尚包含其他因子，例如式（4.56）中的

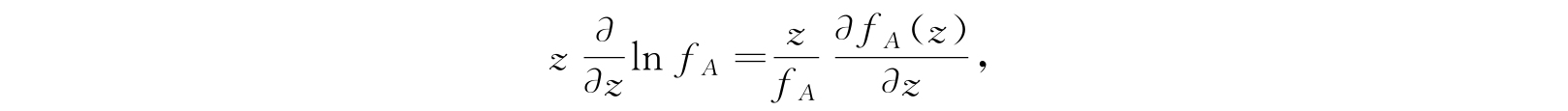
此时上面所讲的关于被积函数的一些性质仍然是成立的（但当被积函数中含有上面这个附加因子的高次幂，如E次或N次，则被积函数的性质是会不同的）. 在效果上我们可以在附加因子中用θ代替z而将其提到积分号外面. 被积函数在正实轴上的极小值的位置z=θ，是方程

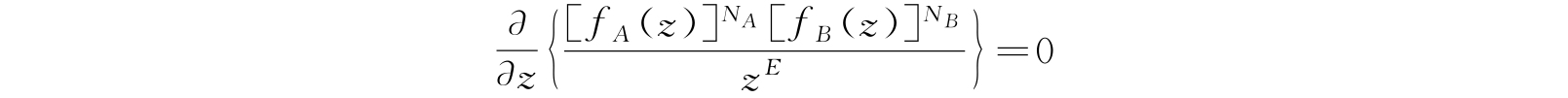
在0与1之间的实根，亦即θ满足方程

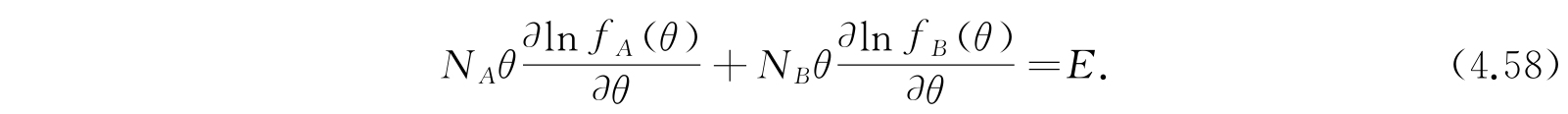
利用这些结果，我们可将方程（4.56）写成

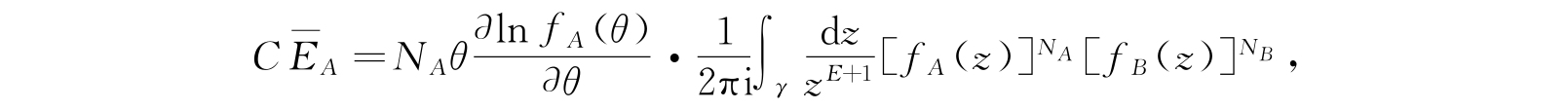
与式（4.55）比较，我们得

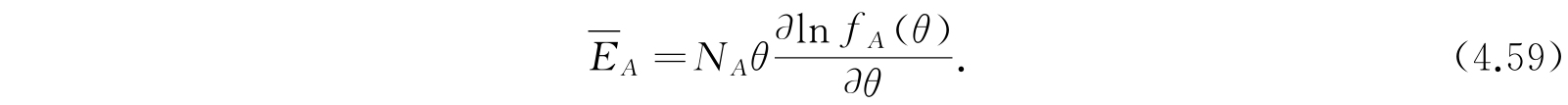
同理，得

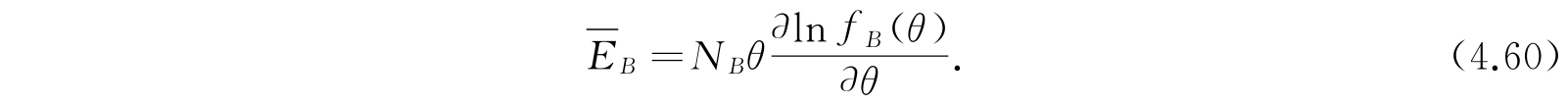
比较式（4.58）、（4.59）及（4.60），我们看到，方程

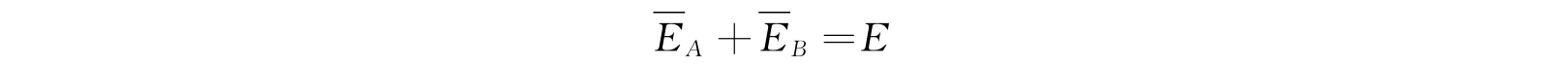
是被满足的. 这些方程确定了在一个大系集内，能量在两组谐振子之间的分配情况.

用同样方法，比较式（4.55）及（4.57），我们得到

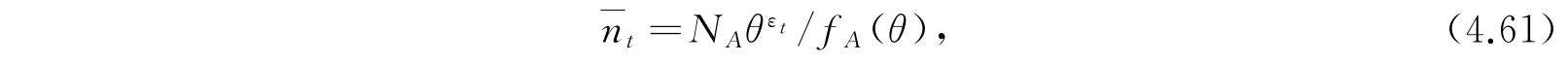
由f _A （θ）的定义，得知 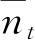满足实质方程

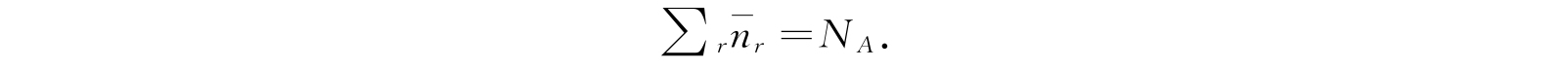
现在我们来讨论，如果考虑到系集的能量值有一小区间，而用式（4.41a）代替式（4.41）时对结果有什么影响. 下面我们即将指出，作为结果的各个公式变化很小，可以忽略不计.

在上一节中，我们曾经讲过，C的值是在

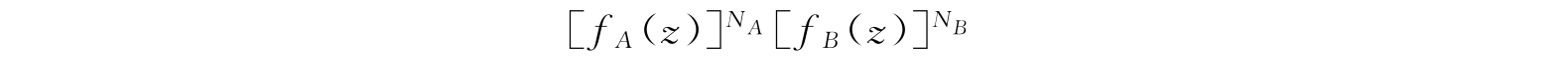
对z的幂次展开式中z ^E 项的系数. 与以上论证的道理一样，可以指出，假如用式（4.41a）代替式（4.41），则C值是上述表示式中z ^E 和z ^E+dE 之间所有z的幂次项的系数之和. 同样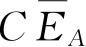， 是在

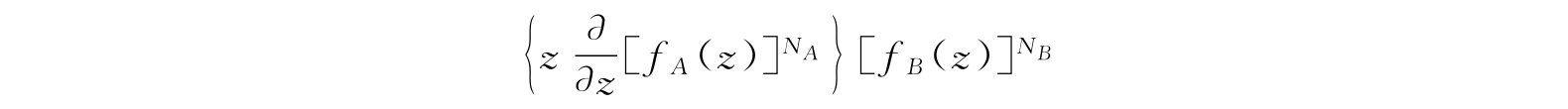
的展开式中z ^E 和z ^E+dE 之间各幂次项的系数和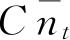， 是在

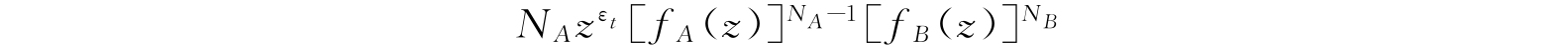
的展开式中z ^E 与z ^E+dE 之间所有项的系数和. 用以前的方法把这些新的表示式表成回路积分进行计算，则式（4.55）、（4.56）及（4.57）为下列各式所代替：

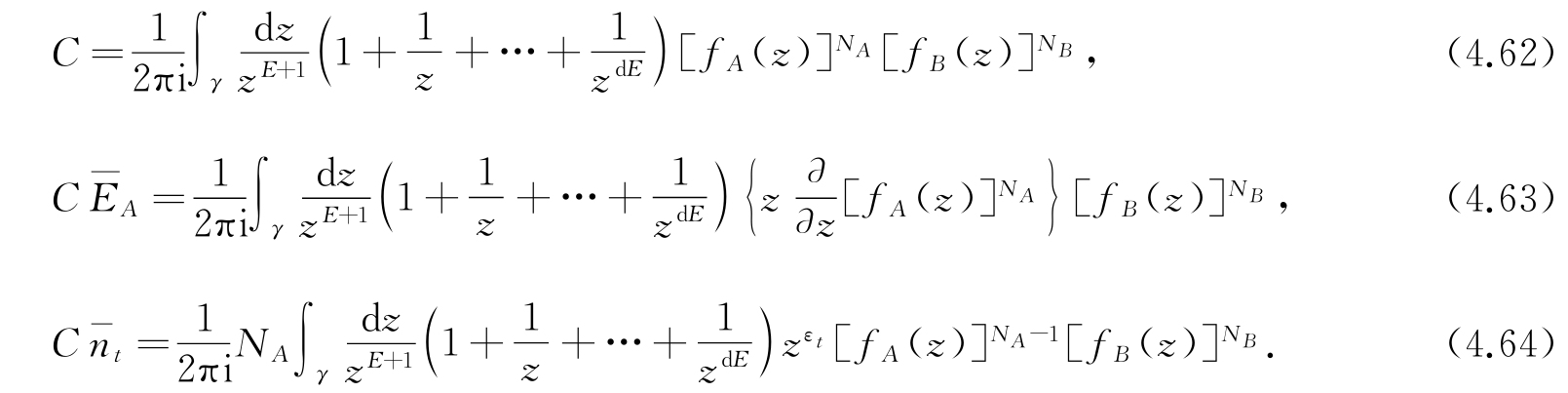
这些新的公式与以前不同的仅在于每一个积分中都包含了一个附加因子

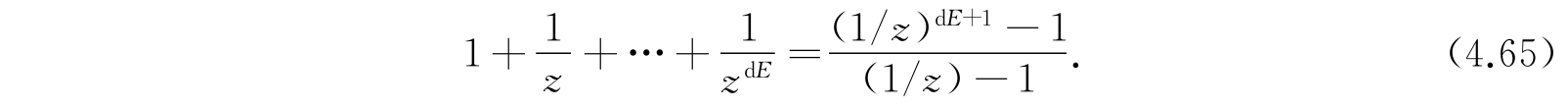
现在可以看到，各个平均值公式特别是 的公式，在形式上绝不因附加的因子而改变，因为附加的因子正好被除掉了. 其唯一的变化是确定被积函数在实轴上极小值位置的公式变了. 现在，公式变成

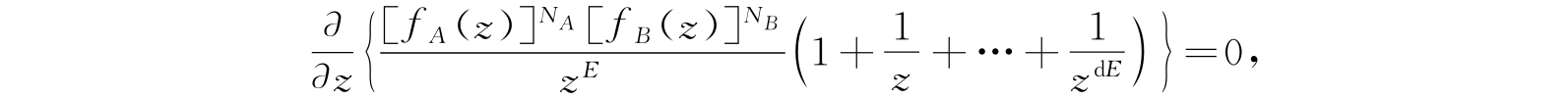
所以式（4.58）要改成

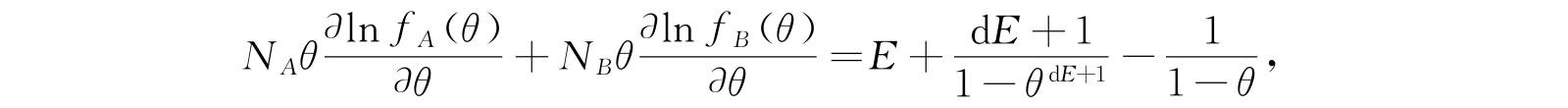
它比式（4.58）在右边多了下面两项：

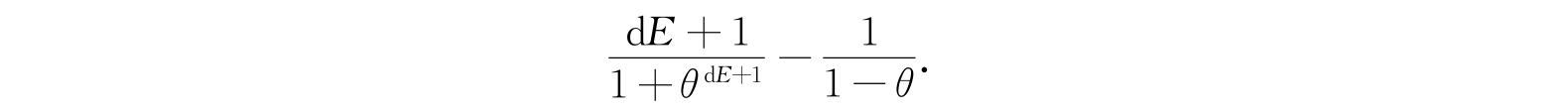
很容易证明：对于0与1之间所有的θ值附加项的值是在（0，dE）区间内. 因此，确定θ的公式可用下列形式讨论：

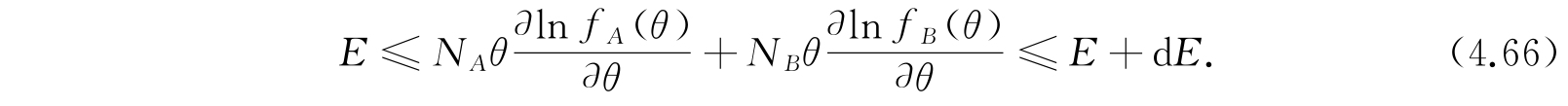
通常总是假设dE≪E. 因此式（4.58）和式（4.66）的差别是很小的.

现在我们已看到，基于式（4.41）的求平均和基于式（4.41a）的求平均并没有很大的差别. 所以以后没有必要再用这些较为普遍的平均. 所有对于确定的能量值的平均公式，都可以用来代替在一小能量区间中的平均公式而不用加以任何修改. zVY/kQbBj/jkVCR7UdpfWKOXG7HeUqMboU4Pfr8lsZ2U53zkWjaR9xWgBY+F+Hkf