




为了叙述简单起见,我们先考虑一个特殊情形,由这个特殊情形,我们可以看到一般问题的特点及其处理的方法. 考虑一个包含有两大组定域线性振子的系集,两组振子的个数各为N A 和N B . 每一A组振子都有一系列权重为1的定态,其能量为ε 0 ,ε 1 ,…,ε r ,…;同样,B组振子也有权重为1的一系列定态,其能量为η 0 ,η 1 ,…,η s ,…. 这里我们再一次指出,我们能够将定态和能量写成各个体系的定态和能量,实际上是由于我们暗中应用了一个假设,即这些体系是近独立的,也就是说,它们绝大部分时间是进行着自己的运动而不受其他体系运动的干扰. 这个假设对于处理由大量基本上独立的(不是完全独立的)体系组成的系集是很重要的,因为如果能够把状态表成各个体系的状态,会使我们的计算大大简化. 与此同时,我们必须假定振子之间一定也要有足够的能量交换,而且要经常地进行着,倘使不是这样,那么这些体系也就不能成为一个系集,因而也就不会有单一的平衡分布律了. 在目前这一特殊情形中,我们可以假想能量交换是由于振子所处的包壳中有少量的自由原子在进行着这一工作,但是这些自由原子的数目比振子的数目少得多,以致它们本身的能量可以忽略不计.
我们的目的是要确定系集的分布律,即确定振子在各个可能的状态上的平衡分布(或平均分布). 每一种分布情况,不论是平衡的还是非平衡的,都可以作为系集的一个统计状态. 由此可见,实际上引起我们兴趣的只是系集的宏观状态而不是微观状态.
如有一组正整数(包括零在内)n r 、n' s ,满足条件
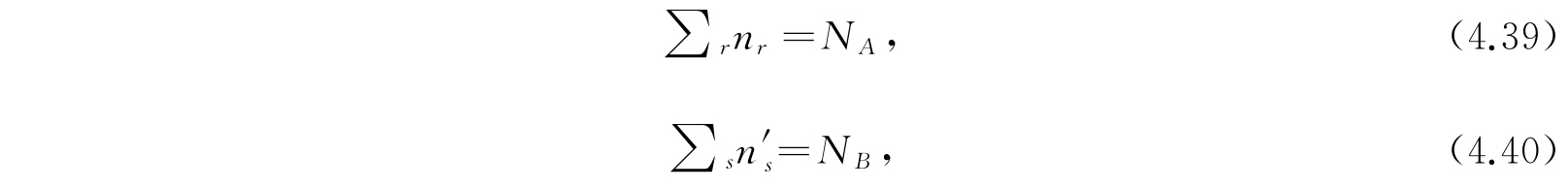
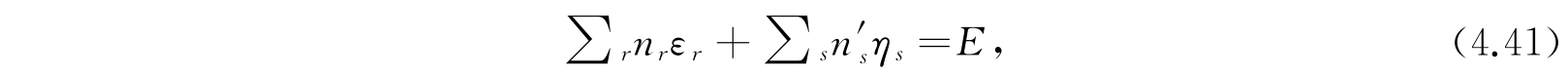
其中E是系集的能量,那么,这一组n r 、n' s 给出系集的一个可及统计状态. 关于可及性的限制,在第3章中我们已经讨论过,然而在第3章中,我们是要限制全系集的能量于一个能量小区间(E,E+dE)中,而不是式(4.41)所表示的限制于一定的能量值E. 因此,按道理,我们不应该用式(4.41)而应该用
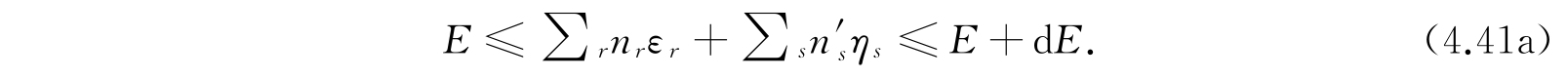
以后我们可以证明,采用式(4.41)或(4.41a),对于结果的影响非常小. 现在为了简单起见,我们先采用式(4.41),这样讨论起来会比较方便.
条件(4.39)、(4.40)及(4.41)表示了几个事实,即体系A的总数是N A ,体系B的总数是N B 及总能量为E. 在式(4.41)中,体系A的能量ε r 与体系B的能量η s 的零点可以各自任意选取;而E的零点取决于ε r 及η s 的零点. 对于给定的N A 、N B 及E,任何一组满足式(4.39)、(4.40)及(4.41)的正整数(或零)n r 、n' s ,都代表系集的一个统计状态. 因为系集是第一种类型的并且体系的权重都是1,因此,这个统计状态的权重是
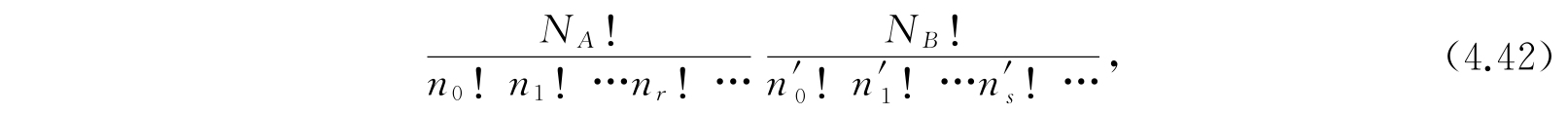
此式只是式(4.36)的一个推广. 总配容数C为
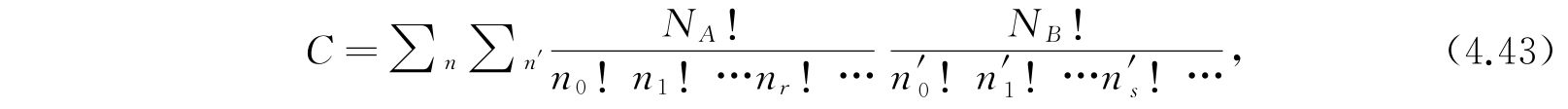
式中的求和号表示对于所有满足式(4.39)、(4.40)及(4.41)的n、n′求和.
对所有的配容求平均,我们可以求得系集的平衡分布律. 这样,我们可以直接写出n
t
的平均值
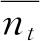 的表示式或者任何与之相似的量的平均值表示式,对于
的表示式或者任何与之相似的量的平均值表示式,对于
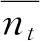 ,由式(4.3),我们有
,由式(4.3),我们有
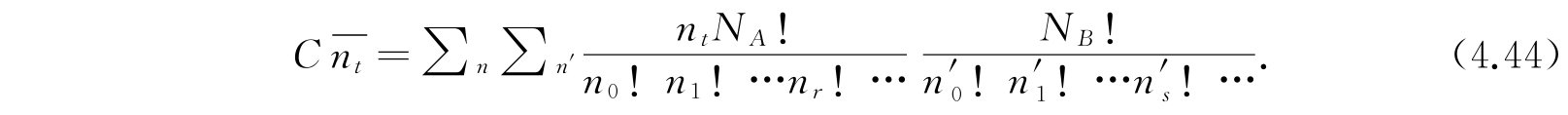
最重要的平均量之一是体系A的平均能量
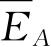 . 对于
. 对于
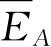 ,有
,有
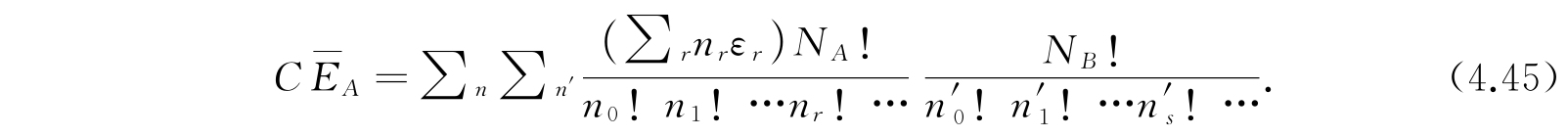
式(4.44)及(4.45)中的求和,都是对于满足式(4.39)、(4.40)及(4.41)的n r 、n' s 求和. 下面我们将指出,式(4.43)、(4.44)及(4.45)这样一些表示式的右方,都是某些简单幂级数的系数. 在下面的数学运算中,如果我们能够假设ε r 、η s 都是某一能量单位的整数倍并且没有公因子,那么,这些运算会简单得多. 这个条件是很难完全准确地满足的,但是我们可以借助于选取一个适当小的能量单位而使它高度近似地满足. 现在我们假设已经选了这样的能量单位. 我们可以证明,即使ε r 、η s 不能满足这个条件,其结果并不受影响.
首先,我们定义一个函数f A (z),称为体系A的 配分函数 :
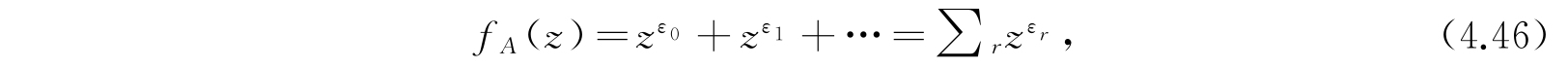
并且考虑它的自乘积
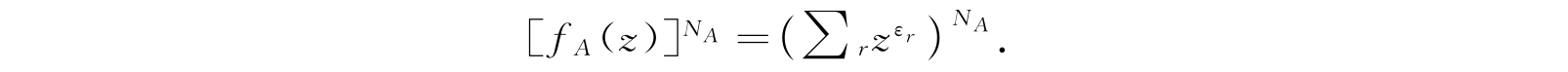
用多项式定理将其展成z的幂次项,其普遍项为
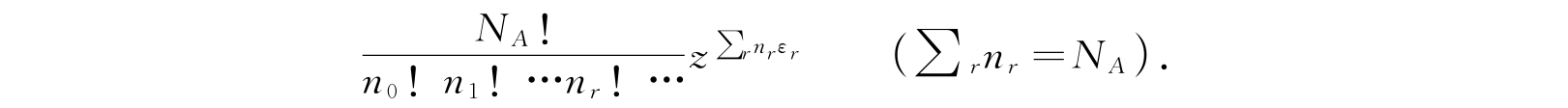
同样,我们定义体系B的配分函数f B (z):
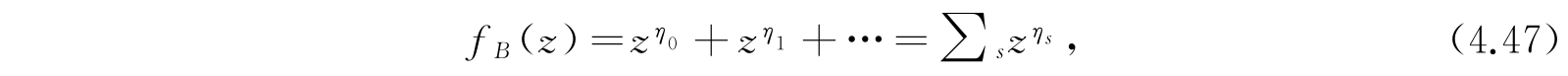
并且将
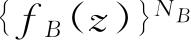 展成z的幂次项,其普遍项为
展成z的幂次项,其普遍项为
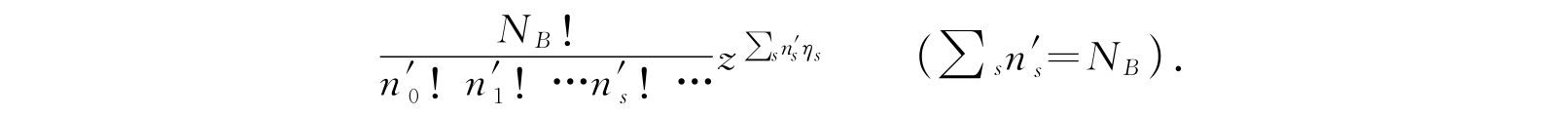
将这两个展开式相乘,我们看到,
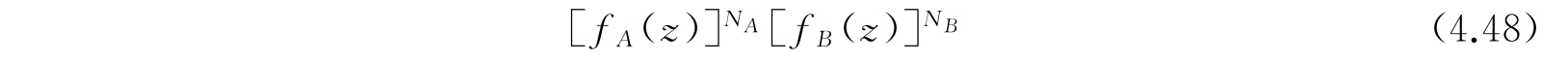
的展开式中,z E 项的系数为
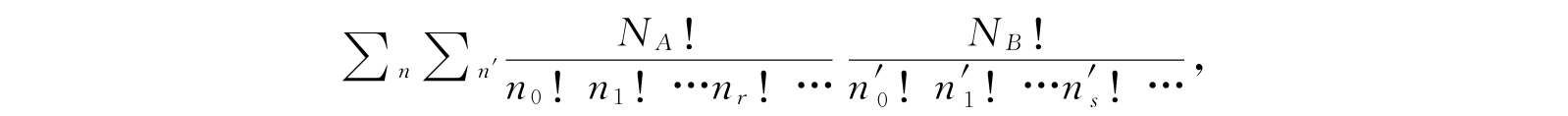
并且也恰好是对满足式(4.39)、(4.40)及(4.41)的正整数(或零)n、n′求和. 与式(4.43)比较,我们看到这个系数就是总配容数C.
同样,对于
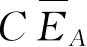 可以得到一个相似的表示式. 我们刚才看到
可以得到一个相似的表示式. 我们刚才看到
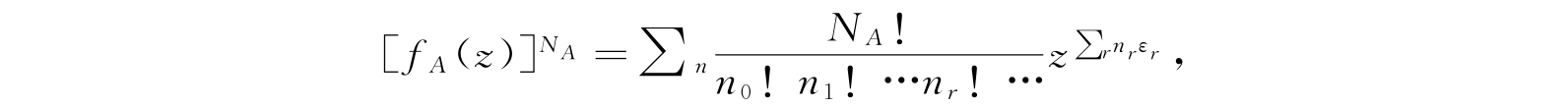
如果我们将等号两边均对z求微商,然后乘以z,可得到
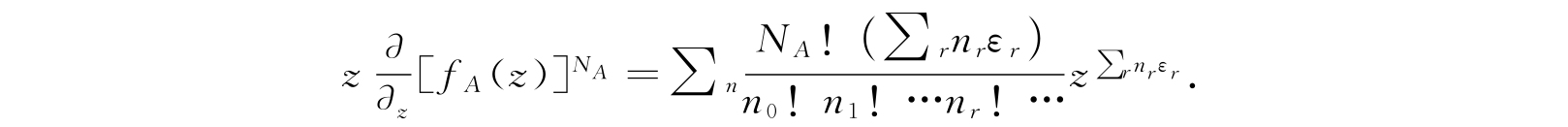
两边再乘以
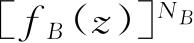 ,得
,得
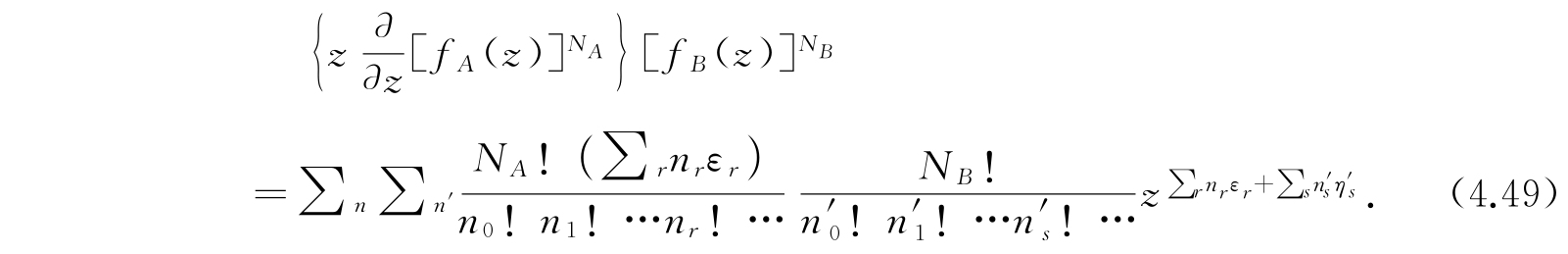
对于满足式(4.39)及(4.40)的正整数n和n′求和. 注意式(4.49)右方展开式中的z
E
的系数并回忆式(4.45),那么,我们看到z
E
项的系数正是
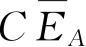 .
.
对于
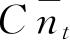 ,我们能够给出类似的公式,由式(4.42)有
,我们能够给出类似的公式,由式(4.42)有
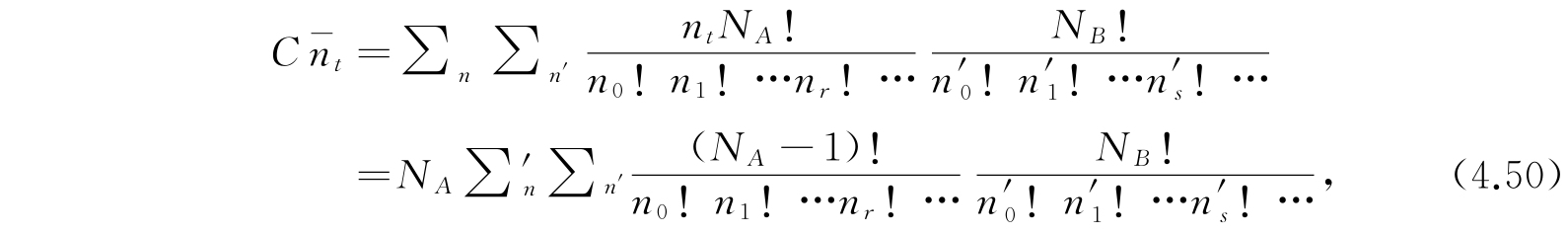
其中
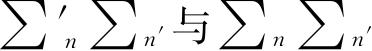 不同,前者是对于满足下列条件的正整数(或零)的n、n′求和:
不同,前者是对于满足下列条件的正整数(或零)的n、n′求和:
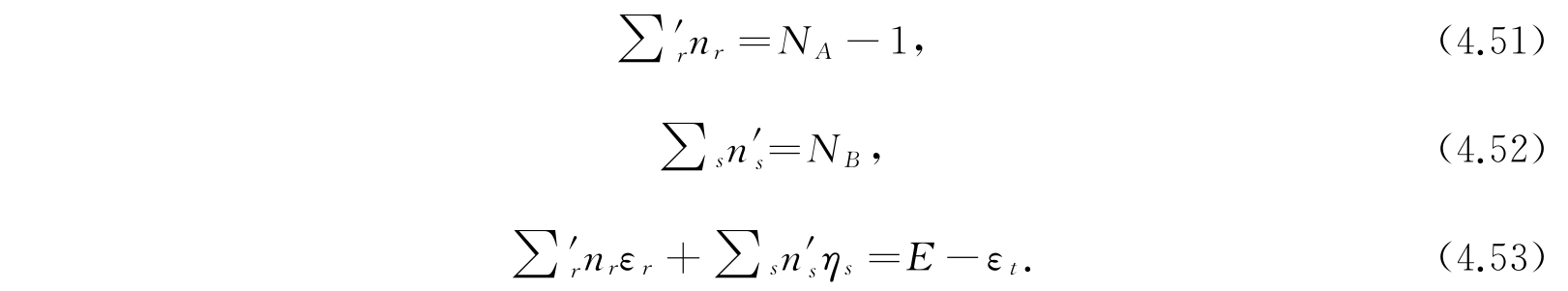
假如我们把函数
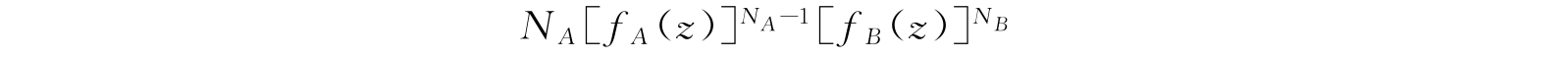
展开成z的幂次项,那么,我们能够发现
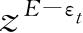 项的系数正是表示式(4.50),而且求和的约束条件亦是式(4.51)、(4.52)及(4.53). 所以
项的系数正是表示式(4.50),而且求和的约束条件亦是式(4.51)、(4.52)及(4.53). 所以
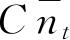 是
是
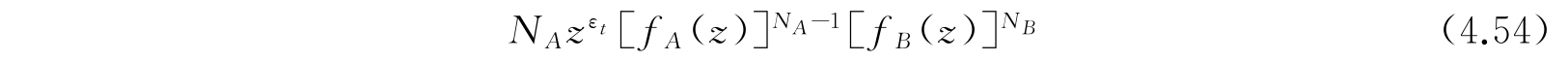
的展开式中z E 项的系数.
到现在为止,我们已经看到,总配容数C、平均值
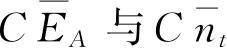 以及其他相类似的量皆可表成某些幂级数的某一项的系数. 下面我们的工作就是要计算这些系数. 最有效而且迅速的计算方法是先把它们表示成回路积分的形式,然后用最陡下降法计算积分的渐近值. 下一节我们将简述这一方法,但我们不讲它的详细证明
以及其他相类似的量皆可表成某些幂级数的某一项的系数. 下面我们的工作就是要计算这些系数. 最有效而且迅速的计算方法是先把它们表示成回路积分的形式,然后用最陡下降法计算积分的渐近值. 下一节我们将简述这一方法,但我们不讲它的详细证明
 .
.