下载掌阅APP，畅读海量书库
立即打开
现在我们来进一步考虑，如何由系集中各个体系的状态计算系集的配容. 在这个问题上，也仅仅在这个问题上，经典的计算结果可能与量子的计算结果有巨大的分歧. 回忆在第3章中我们所讲过的定域系和非定域系之间的差别. 我们知道，定域系组成的系集和非定域系组成的系集，它们的可及态（配容）的数目是不相同的. 现在我们对两种系集各举一个简单例子来讨论如何计算配容. 在这两个例子中，我们都假定体系是非退化的.
第一类系集，定域系系集. 考虑一个系集，它是由N个相同的、在系集内有固定位置的线性振子（不一定是谐振子）组成的. 例如是一些适当地束缚于固体中的原子上的电子. 各个振子皆有一组不连续的定态，它们由量子数r来表示，r的可能值为0，1，2，…. 原子α所束缚的电子a处于第r个量子态时的本征函数可写作
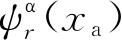，此处x
a
表示电子a的坐标. 设处于量子数为0，1，2，…，t的状态上振子的数目各为n
0
，n
1
，…，n
t
，则对应于这一分布有许多系集状态，我们把这些系集状态看作是一个状态，而它的权重等于这一群系集状态的个数. 如式（4.6）所示，这一群本征函数的个数是
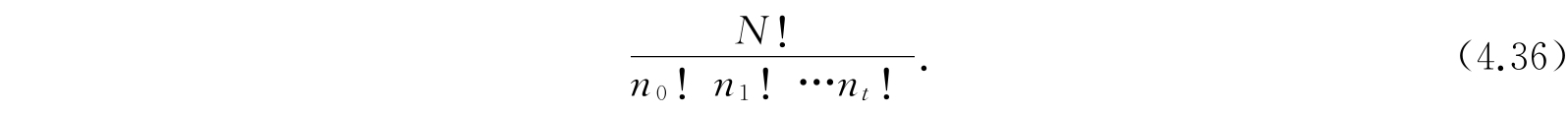
我们举出其中的一个：
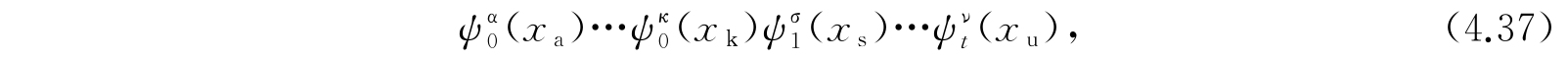
其中因子ψ 0 共有n 0 个，ψ 1 共有n 1 个，依次类推，一共有N个因子，因此这是所应考虑的一个系集状态. 我们若将其中电子a的和电子e的能级交换，则我们得到这一群系集状态中的另一个：
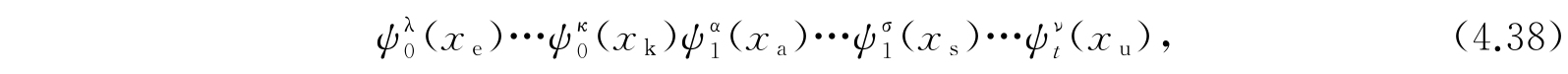
其中各种因子的数目仍没有改变. 因此，我们将电子的能级交换一共可以得到式（4.36）那么多个本征函数. 应当指出，事实上，这里我们还应用了一个假设，即：并不是只限于处于系集的某些位置上的振子才能有某一激发度. 在这些本征函数中的电子都是属于同种原子的，但是这些本征函数对于电子却不是反对称的. 然而如果我们像3.9节及3.10节中所讲的，将N个电子在N个原子上交换，那么，每一个如式（4.37）的本征函数都能够组成一个对电子是反对称的本征函数，而且只有一个. 因此式（4.36）所给出的本征函数是正确的，虽然在计算它的时候，我们并没有考虑到对称性的要求，而是把每一个电子都看作是永远束缚于它所在的原子上.
第二类系集，非定域系系集. 考虑一个系集，它是由N个在给定体积的包壳中自由运动的电子（或其他种体系亦可）组成的. 现在本征函数中不再出现标志着体系所处的特定区域的附标α，…，κ，…. 令n 0 ，n 1 ，…，n t 仍是处于由量子数r所决定的各状态上的电子数，则对于一个分布，系集的不考虑对称性要求的本征函数仍有式（4.36）那么多. 但是当我们需要构成对系集中所有的电子是反对称的本征函数时，只有当每一个n都等于0或1时，才能构成一个，否则就没有反对称本征函数. 对于有正对称要求的体系组成的系集，无论n等于若何，总能构成一个正对称本征函数. 以上这些都是在3.6节中讲过的.
现在我们已经具备了计算这两种系集平均性质的基本知识. 以下即将求系集的平衡性质，首先要讨论定域系系集.