4.2　几个简单体系的状态的权重

在2.4节中已经指出，一个频率为ν的谐振子的能态为

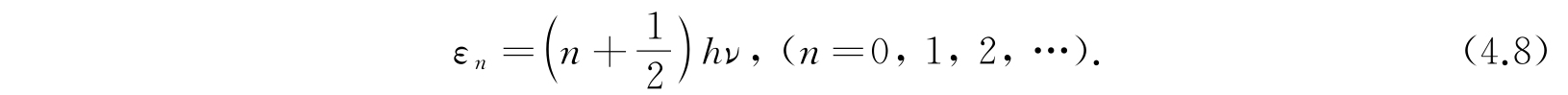
考虑经典相空间中的任一个可能的轨道，其方程是

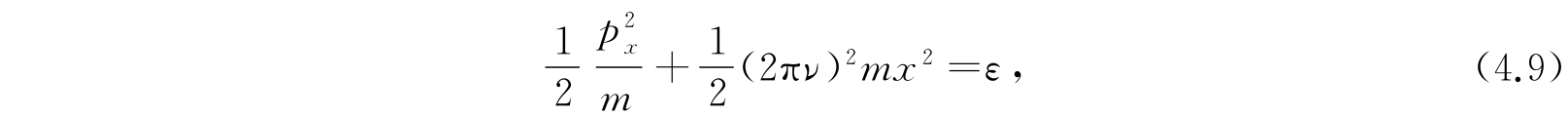
这是一个半轴 的椭圆. 它所包围的面积是

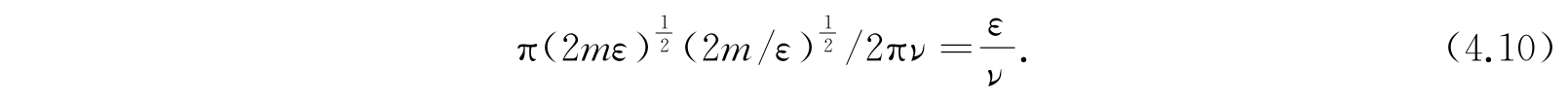
在经典理论中，所有满足方程（4.9）的轨道都是可能的，但在量子理论中，ε/ν的值只能取 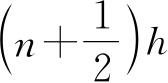，而n只能是正整数或零. 量子理论中相邻轨道之间的面积是h. 因此，当量子数n大时，可能的轨道几乎密合在一起，但仍然是被面积h所隔开的，此时，与每一量子态对应的相空间单元的面积为h. 于是我们对于谐振子验证了极限定理（在3.5节中我们曾经叙述过这个定理）.

现在讨论二维各向同性谐振子，其经典能量方程为

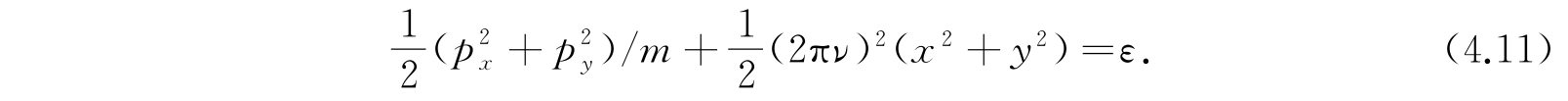
对应的薛定谔方程为

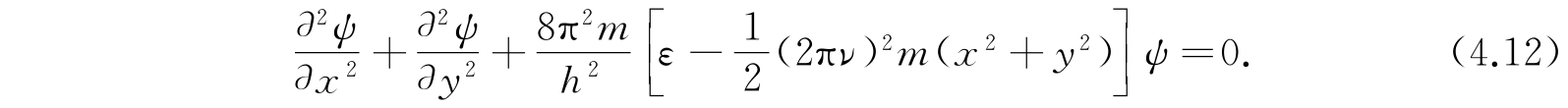
将此方程分离成变量为x及变量为y的两个方程. 我们看到本征函数的形式为

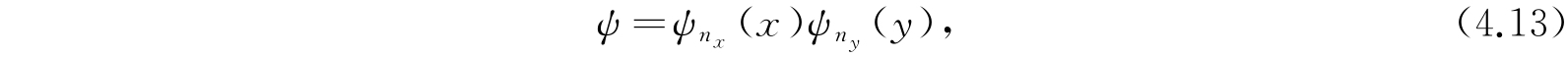
其中 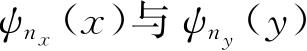是具有量子数n _x 和n _y 的谐振子的本征函数. ψ对应的能量为

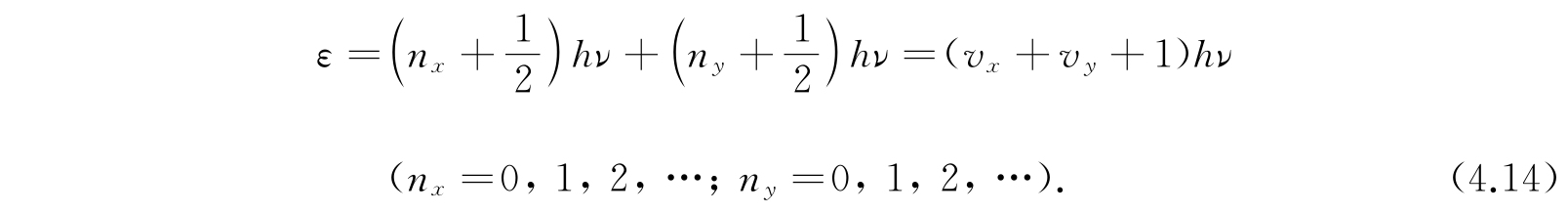
令n _x +n _y =n，则每一个n对应于一个不同的能值. 但每一个n值可以由n _x 和n _y 的（n+1）种不同的组合来得到. 因此，ε=（n+1）hν给出的ε值是对应于（n+1）个不同的本征函数. 所以能级ε=（n+1）hν的权重为n+1. 如要验证极限原理，只要我们能够指出：与一个量子能级相关联的经典相空间体积，与量子数n很大时和值（n+1）h ² 没有很大差别. 在相空间（x，y，p _x ，p _y ）中，能量等于常数ε的曲面所包围的体积为

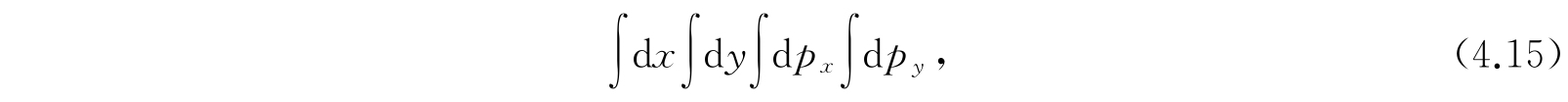
积分区域为

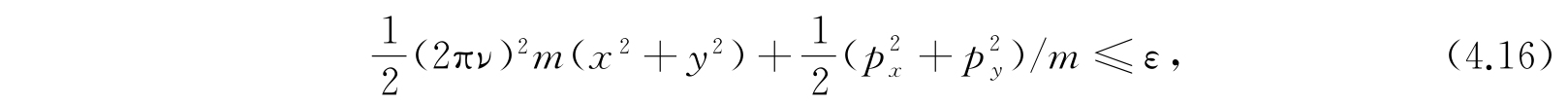
用代换

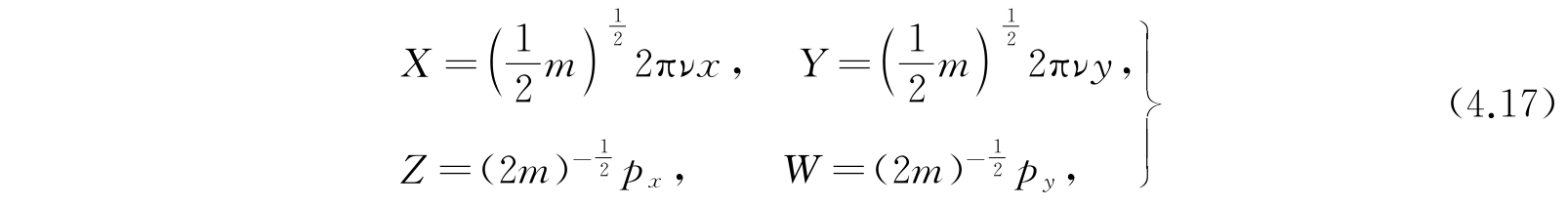
则积分（4.15）变为

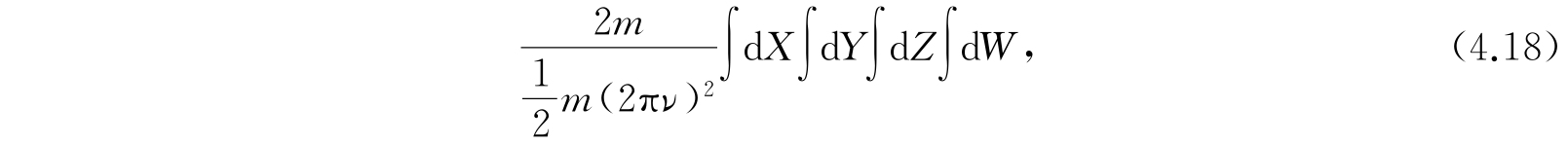
积分区域是半径为 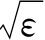的四维球面所包围的空间，即

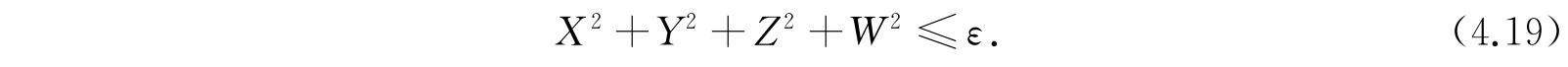
按照半径为r的N维球体积的一般公式：

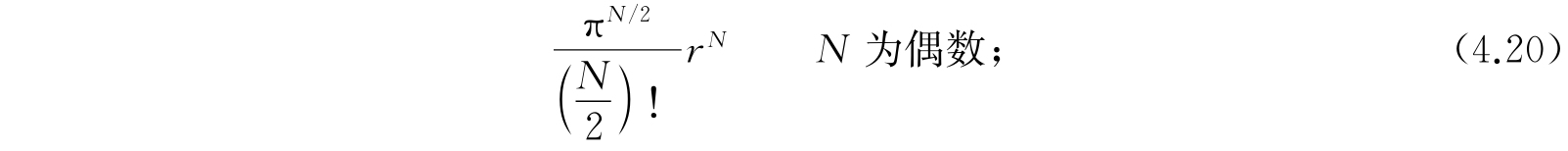
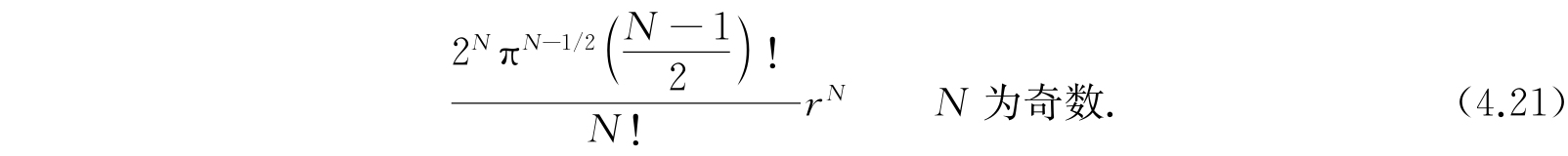
对于我们的情况，应用式（4.20），令其中的N=4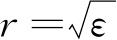， ，则积分（4.18）为

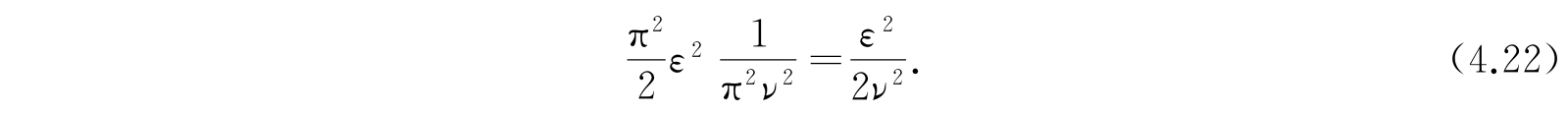
在曲面 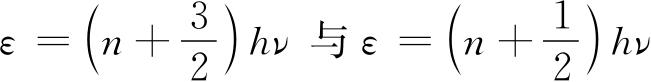之间所包围的相空间体积，即为能量ε=（n+1）hν的量子态所对应的体积，为

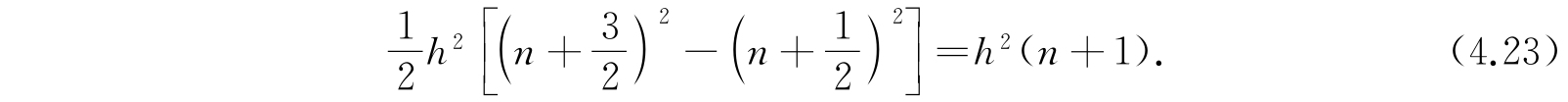
这是与极限定理相符的.

对于三维各向同性谐振子，用同样的方法得知，相应于能量

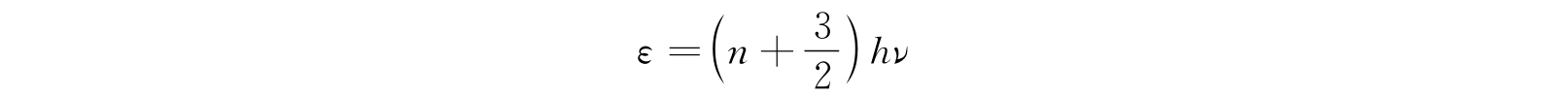
的本征函数的数目等于使n _x +n _y +n _z =n时n _x 、n _y 、n _z 为正整数或零的解的数目. 现在我们计算这个数目，令n _x 取值m，于是n _y 可能取的值就有（n+1）-m个. 故本征函数的数目为

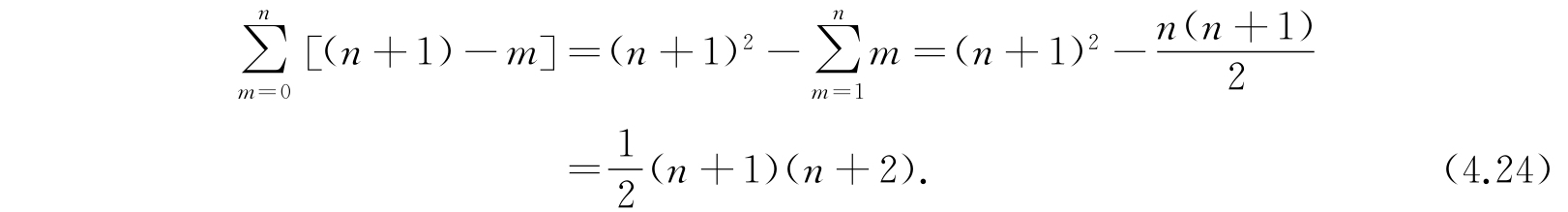
在经典相空间中，能量等于ε的曲面所包围的体积是

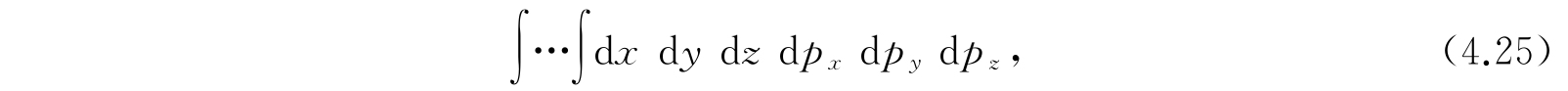
积分区域是

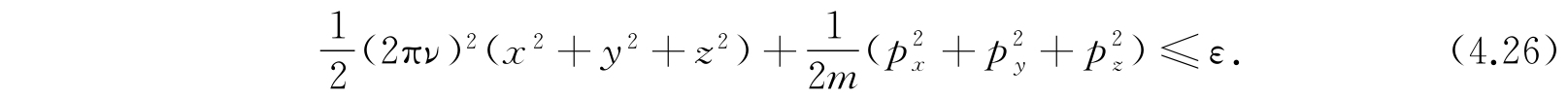
利用与式（4.17）类似的变换，可以证明积分（4.25）等于

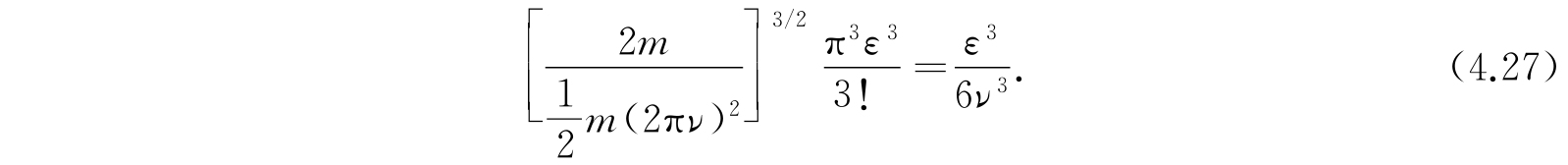
在曲面

ε=（n+2）hν　与　ε=（n+1）hν

之间的相空间是与量子能级 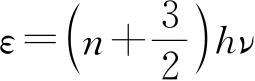相对应的，其体积为

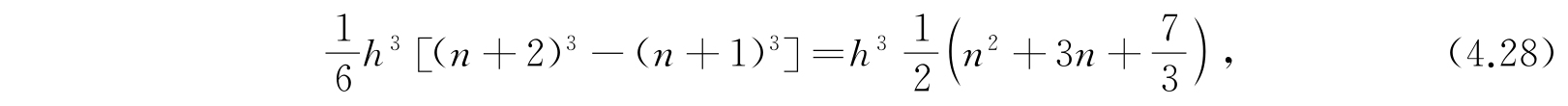
当量子数n大时，它与 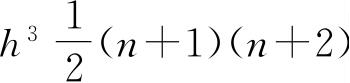相差不大，这正与极限定理相符合.

最后一个例子，我们考虑轴对称的但没有绕轴自旋的刚性转子. 令A为横向转动惯量，θ、ϕ为轴的球极坐标，其共轭动量为

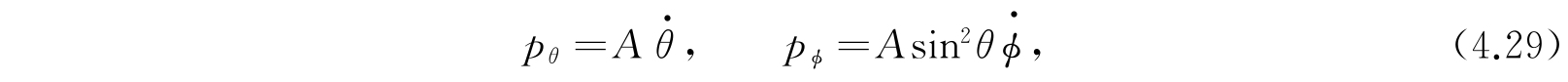
其经典能量方程为

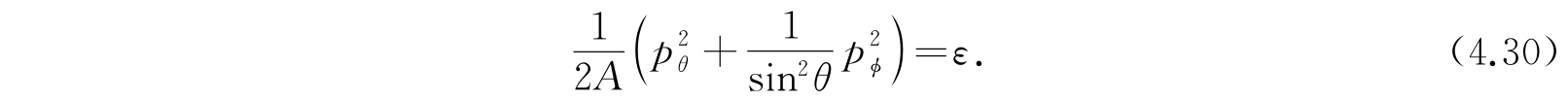
由2.15节我们知道，在量子理论中，能量ε的可能值为

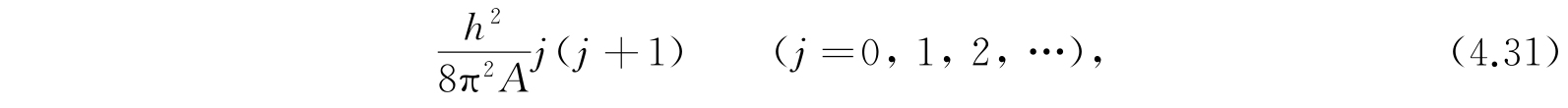
与第j个状态相对应的本征函数有2j+1个. 因此，其权重为2j+1. 能量等于常数ε的曲面所包围的相空间的体积为

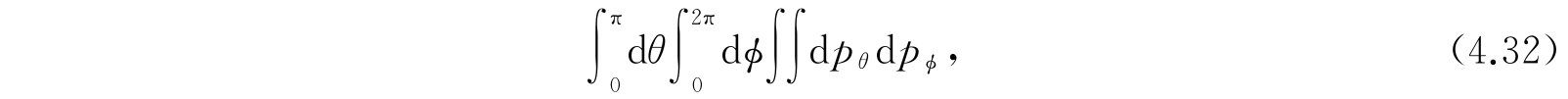
其中对p _θ 、p _ϕ 积分的范围为

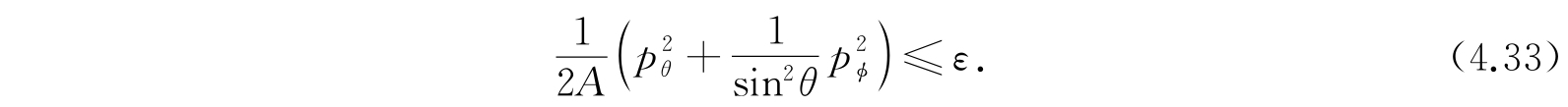
对p _θ 、p _ϕ 积分后，得到半轴为 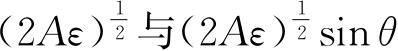的椭圆，面积是2πAεsin θ. 因此积分（4.32）变成

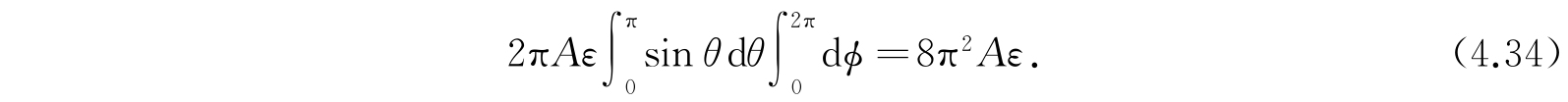
在两个曲面

之间的相空间体积，亦即与量子态ε=j（j+1）h ² /8π ² A相对应的相空间单元是

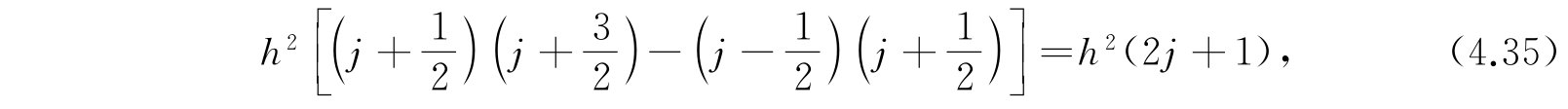
这是与极限定理相符合的. RrUemBoXp9sJmvX2Zc2d8lL8w2vhXskfL0xFcok7FTMynHfz7Iu5uu3oxSj/bv/G