下载掌阅APP，畅读海量书库
立即打开
在第三章中我们定义系集的可及态（配容）是系集的彼此线性无关的本征函数，并且也讲了在用求平均的方法确定平衡态时，每一个可及态（配容）均给以单位权重. 这就是说，某一量Q的平均值
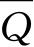应如下计算：
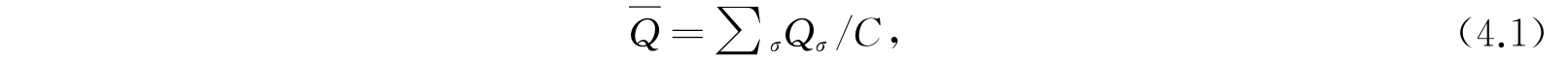
其中Q σ 表示配容σ所对应的Q值，∑ σ 是对所有的配容求和，C表示总配容数：
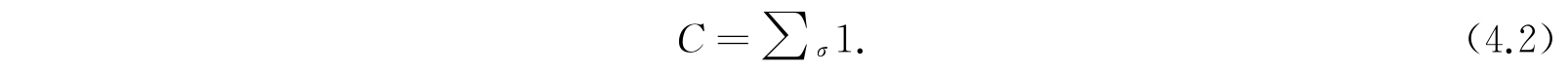
式（4.1）和（4.2）常可以整理成其他的形式. 首先，在很多场合中，可能会有Ω σ 个不同的配容在很多问题上具有同一个彼此不能相区别的性质，例如有同样的Q值. 此时，我们可以在式（4.1）及（4.2）的求和号下将具有同样Q值的配容先加起来组成一个配容群，这样式（4.1）及（4.2）可分别改写为
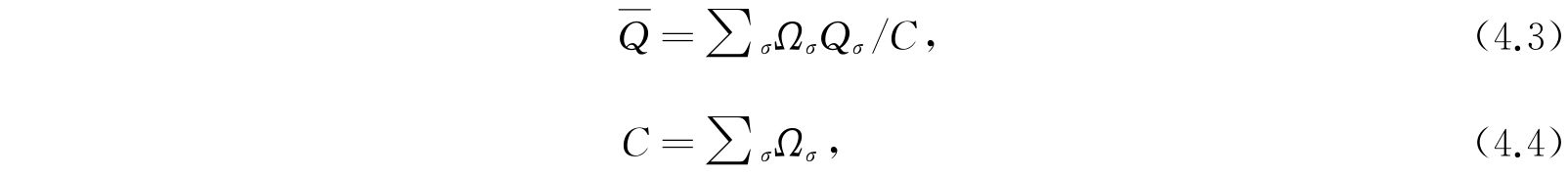
现在是对所有的配容群求和. 由于配容群中各配容的性质彼此不能区分，而我们也不想去区分它们，所以为了简单起见，我们时常把这一群配容看作系集的一个单个状态，其权重为Ω σ .
现在我们来讨论权重Ω
σ
. 因为我们所要讨论的系集都可以当作近独立体系的系集处理，即可以近似地认为体系之间没有相互作用. 所以确定系集的本征函数与能态的薛定谔方程可以分离成对于各单个体系的薛定谔方程. 因此，系集的本征函数Ψ可用各体系的本征函数ψ的乘积构成. 我们知道，对应于体系的一个能态可能有
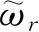个不同的本征函数，这时，我们仍然把这些本征函数看作体系的一个单个状态，其权重为
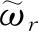. 为了方便，我们称
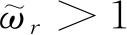的状态为退化的，称
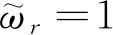的状态为非退化的. 假若有一个系集包含N个近独立体系，我们考虑系集的这样一个状态：在权重为
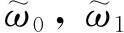，…的各个单个体系的状态上，体系的数目各为n
0
，n
1
，…，而且各状态上的体系都是指定了的. 假如没有特殊的可及性限制，则这个系集状态所对应的配容数，亦即此状态的权重为
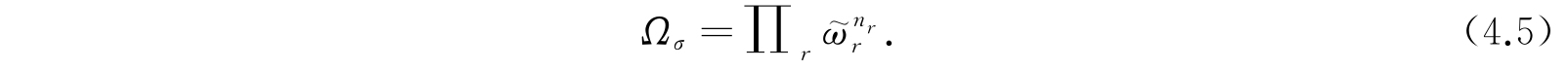
式（4.5）是这样得到的：我们知道，某一状态上的体系可以任意取其可能的本征函数，而且某个体系取哪一个本征函数并不受别的体系所取的本征函数的影响. 因此，在权重为
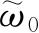的状态上，第一个体系取本征函数的方式有
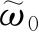个，第二个体系也有
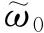个，所以两个体系同时选取本征函数的方式有
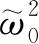个. 共有n
0
个体系，所以共有
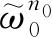个方式. 同样，对于权重为
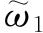的状态共有
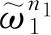个方式，对于其他状态也是如此. 因此，与一个系集状态对应的可能的独立的本征函数共有
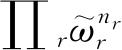个. 在以上的讨论中，实际上我们还用了一个假设，即这些体系在物理上是可以用某种方法加以区别的，因此，本征函数ψ（1）ψ′（2）与ψ′（1）ψ（2）是不同的，它们各导致不同的配容.
式（4.5）是当各状态上的体系都是固定的时候得到的，对应于这一分布状态，配容数是由式（4.5）给出. 如果各个状态上的体系不是固定的而是可以由N个体系中任意选择的，则与这个分布状态相应的配容数要比式（4.5）给出的大，现在配容数是
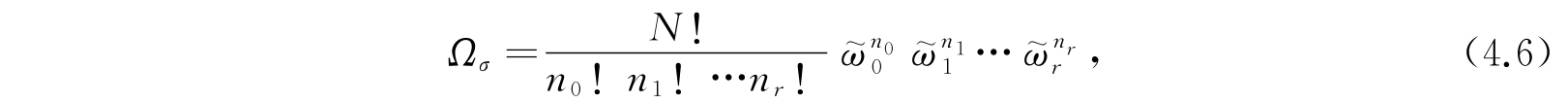
其中因子
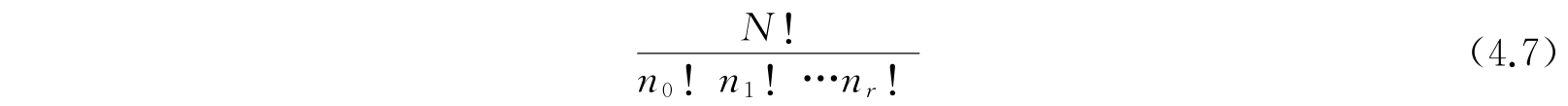
是由N个体系组成数目为n 0 ，n 1 ，…，n r 体系系集的组合数. 自然，在以上的计算中，我们都没有任何附加的可及性限制.