




前节的实际考虑主要适用于气体系集或者适用于具有下列性质的一些系集或系集的某些部分,在这些系集或系集的某些部分中,相似体系必须给予相等的地位而一律对待,也就是说,它们的状态要用来自一个公共来源的本征函数表示. 在同一包壳中的气体原子或分子,在一单个原子中或在一小块金属中的电子就是这种例子. 关于电子、质子或中子的个体规则自然毫无例外地可以应用到所有的物质上和所有的系集上,并且在以上节所述的情况导出实用的第二级规则. 当然,这种第二级规则的应用必须限制在上面几节决定的范围内,如果我们不需要把所用的本征函数都认为是出于一共同的来源,而认为可以辨认它们,这时候,第二级规则还能进一步简化.
这些更进一步的限定或许可以从下面的例子来了解. 让我们考虑一个包含两个不同包壳的系集,其中每一个包壳都包括着很多电子. 我们可以设想,电子能够从一个包壳到另一个包壳中去,但不那么容易. 平衡时电子将在两个包壳中以一定比例分布着,确定这个比例就是我们任务的一部分. 但是当我们可以近似地认为电子态是属于这一包壳或另一包壳的描写的时候,这两个包壳可以设想对于电子态的描写来说是有足够区别的. 让属于其中第一个包壳的电子态具有本征函数ψ r 而相应的能量为ε r ,属于另一包壳的电子态为ψ' r 而能量为ε' r . 让我们设想系集包括五个电子,而考虑到它们的分布是有三个电子在第一包壳中,所占据的态分别用ψ 1 、ψ 2 、ψ 3 来代表;而在第二个包壳中的两个电子所占据的态分别用ψ' 1 、ψ' 2 来代表. 当然,只存在着系集的一个可及态,它满足对所有的电子本征函数是反对称的要求. 这个态就是由下面行列式所给出的本征函数所表示的:
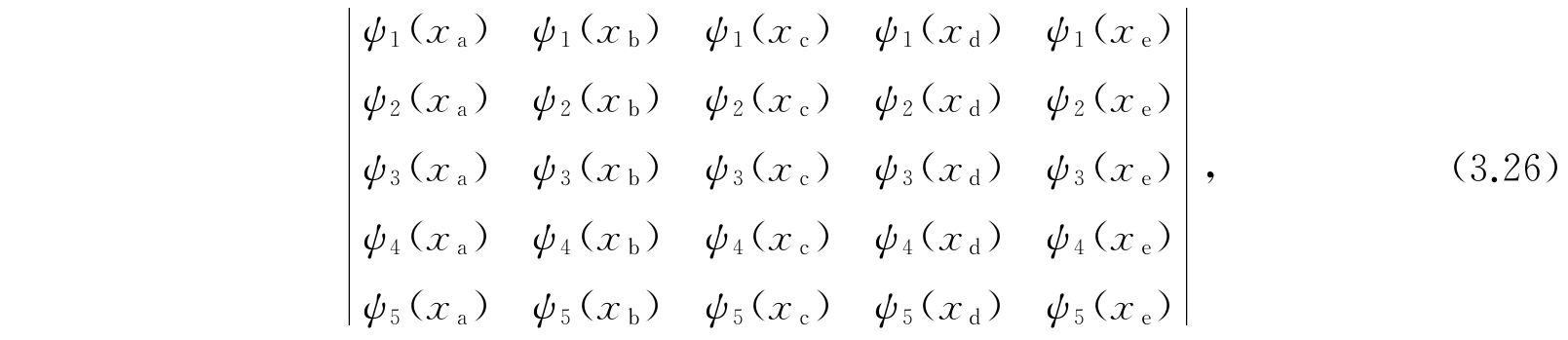
其中坐标x的下标a、b、c、d、e指的是电子. 然而设想代替引进这种完全反对称性,我们考虑电子a、b、c确实属于第一个包壳,而电子d、e属于另一个包壳. 因此,如果构成一个关于系集的本征函数,它满足:有关每一包壳中的电子的因子,对于那个包壳的电子说来,分别是反对称的要求,则我们又恰好只得到一个本征函数,即
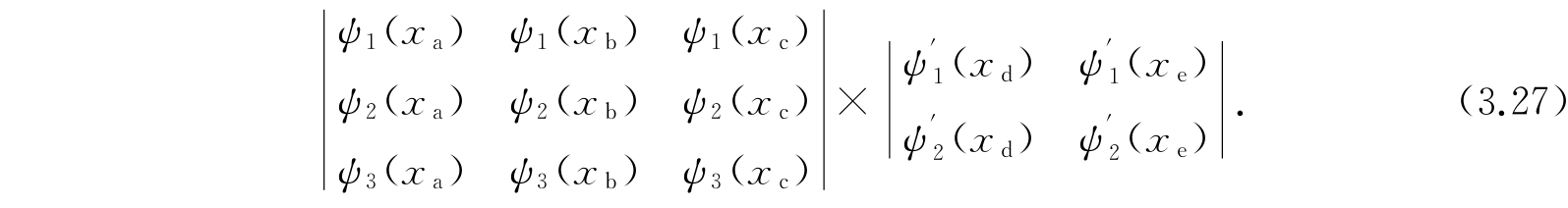
而正如我们已经看到的,只存在一个可及态. 能够证明(而实际上这几乎是很明显的),这种等价是十分一般的. 如果系集有几个可以认为是不同的部分,其中每一个部分都包含着一定数目的相似体系,那么在清数系集的可及态时,只要使系集的本征函数对于在系集的每一不同部分之中的相似体系,在交换时满足对称性要求,这就能保证系集可及态的清数是正确的. 在这种清数中,对于在不同的部分或包壳之间体系的任何交换是不必考虑的.
我们可以把对称性的要求更进一步简化. 在某些系集中,不同的部分和包壳的数目可以合法地增加到这样多,以至于我们到达了这样一种限度,其中每一个体系属于它自己的不同包壳或位置. 在晶体格子中的原子就是一个例子,因为晶体中的原子在一次观察或实验的时间内是不会互换位置的. 系集的每一不同部分现在有它自己所有的一个体系,而如果我们应用前述的规则,只要我们保持每一体系固定在它自己的位置上,但不使它担负其他的对称性要求,这样就可以正确地清数系集的可及态. 如果态可以这样计算而并不要求一个更多的对称性限制,则这样的一个系集或系集的一部分称为 定域体系的系集 ,或简称为 定域系系集 .
对于这样一些系集缺乏对称性要求的一个重要后果是可及态的量子清数,全同于我们长久以来熟知的经典清数. 假设这样一个系集的固定体系具有能量ε 1 ,ε 2 ,…的态,它们是非退化的,每一个占有一个本征函数. 这样的系集的分布律应当告诉我们有多少体系(总数是N)在每一态中平均地被发现. 关于这种研究,我们将在第四章中介绍. 在那里,我们要求知道相应于某一种状态下的系集有多少可及态,在这种状态下,n 1 个体系具有能量ε 1 ,n 2 个体系具有能量ε 2 等. 这个可及态数目显然是N个体系被分成很多群包含n 1 ,n 2 ,…成员的数目,而n 1 +n 2 +…+n r =N. 这个数目算出来是
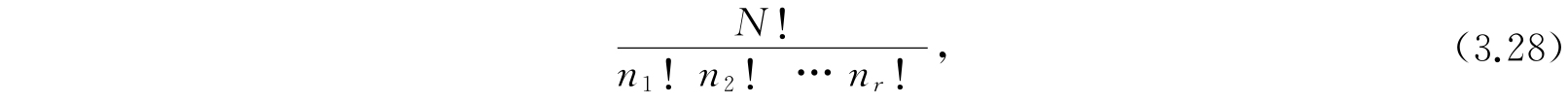
因而它是所要求的具有给定能量分布可及态的数目.
对一个定域系可以用式(3.28)算出所有n值的经典可及态的数目,这个数目不同于由对称性限制的在一单个包壳内的一个相似体系的系集的可及态数目,这两者之间物理上的差异可以说明如下:在一个包含相似体系的包壳内,也就是说一个 在这里 的体系有某某一个能量而另一个 在那里 (在包壳之内)的体系有某某一个能量,按照描写态的本征函数看来是没有任何物理意义的. 但在定域系内, 在这里 和 在那里 仍然是具有物理意义的. 由定域体系组成的系集的体系 在这里 处在第r态中,在物理上是和体系 在那里 处在r态中是有区别的,因而算作处在不同的态中. 用本征函数的话来说,这样的定域特性可以通过下面的事实显示出来,即:不同的本征函数实际上是非重叠的,也就是说,某处只某一类体系可以出现,而别的类型的体系则是不会出现的. 在我们的两个包壳中,有五个电子的例子中就意味着ψ 1 (x d ),ψ 1 (x e ),ψ 2 (x d ),ψ 2 (x e ),ψ 3 (x d ),ψ 3 (x e ),ψ ′ 1 (x a ),ψ ′ 1 (x b ),ψ ′ 1 (x c ),ψ ′ 2 (x a ),ψ ′ 2 (x b )和ψ ′ 2 (x c )实际上是零. 因此方程(3.26)和(3.27)的本征函数实际上是等价的.