下载掌阅APP，畅读海量书库
立即打开
我们知道，直到现在为止还没有一个完整的理由来解释为什么在自然界中对于某一种特定体系的系集，只发现一群本征函数，或者是这一群本征函数而不是另外一群本征函数. 要决定专有的群，我们还必须求助于观察和实验，而专有的群是随体系而不同的. 我们相信，所有物质的系集可以正确地分析成由电子、质子、中子组成的系集，这至少对于热力学的通常要求是合适的. 对于这些体系，在每一种情形下，专有群确实都是 反对称的 . 关于电子，这可以从电子相互作用定律必须体现泡利不相容原理这个事实得出. 根据这个原理，在任何一个原子中的两个电子永远不可以占有相同的四个量子数，或者正如我们现在所说的永远不可以有相同的、包括自旋的本征函数. 对A群系集的本征函数来说，在这个群中没有一个本征态有两个体系具有相同的体系本征函数，实际上，A群是唯一具有这样性质的群. 因为对于任何一个原子中的电子集团的本征函数是属于A群的，人们必须设想，这是由电子的性质所致，而且可以设想，每个系集中电子的本征函数是属于A群的. 对于质子的证据要少些，但依据氢带光谱的解释和在低温下氢的转动比热理论可以作出同样清楚的结论. 对于中子的证据间接一些，但是仍然是正确的，主要从研究氘核的性质和氘的转动比热得出. 在整个下面的讨论中，我们将假设这些对称性的要求. 支持它们的统计论据可以在以后所讲到的应用部分中找到.
正像我们以前所说的，因为所有的系集都能够分析成一些电子、质子和中子，因此，我们能够正确地算出共有多少个不同的态（这些态的本征函数对电子、质子和中子分别是反对称的）. 每一个这样的态称为一个 配容 . 对可及性而言，我们不知道还有什么更加绝对的限制，而从统计力学由于有了这个限制所得到的成功看来，也不需要再加什么其他的限制. 然而我们在任何时刻，在特殊的问题上可以碰到部分的限制，这些限制对于适当的时间范围内和绝对的限制起同样的作用. 氢和氧的气体混合物的亚稳平衡就是一个这样的例子，这个例子我们在前面已经讲过. 其他的例子还可以在研究普通气体（像氧和氮）的比热中遇到，当振动态和平移及转动之间能量交换很慢，以至于在声波中的迅速绝热压缩中，每一振动态表现得好像它的振动能是一个运动常数，因此这些给定振动量子数的分子在一气体混合物中仿佛是不同的气体成分. 我们还会碰到其他的例子，而最令人注目的例子之一是在低温时研究物质性质中碰到的. 在那里，由于可以促成交换的力十分小，总核自旋等于零的分子与总核自旋等于单位核自旋的分子只是慢慢地相互转换，因而，对于通常的实验气体表现的行为，好像是具有不同的转动比热的两种不同的气体的混合物，除非这种转动被适当地催化以后才会改变这种状况.
我们现在已经彻底描绘了一般情况下的条件：这些条件可以限制到或没有限制到一个量子态（或相空间域）是不是可及的. 通过以上关于可及性的分析，现在我们可以把在3.4节中叙述过的求平均的规则用更好的、更精确合用的形式重新表示出来.
如果考虑了建立起平衡所必需的时间长短，那么，就可以算出一个系集的所有不同的可及态或配容. 其中每一个用一个符合于指定能量或能量间隔的线性独立的本征函数来表征. 系集的任一性质Q的平均值
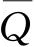可以用来表征遵守特定条件的系集的平衡态，而且它可以由对所有这些可及态以相等的权重（都是1）求平均来得到，形式上即
