下载掌阅APP，畅读海量书库
立即打开
在我们刚才描述过的这类经典系集中，除了能量之外，在某些情形下可以有其他的不变积分存在. 系集的线动量和角动量的分量是不受体系之间相互作用影响的，并且在不受外界影响的时候是守恒的. 因此它们也是这种不变积分. 可以想象，也许还有其他这类的不变积分. 任何一个这样的不变积分对于相空间中代表点的轨迹有着深远的影响. 正像我们以前所表明的，每一个不变积分都是用下列关系表示的：
F（x，p x ）=常数. （3.5）
例如，在一个由质量为m的简单粒子群组成的系集之中，线动量的x分量为常数的表示式是
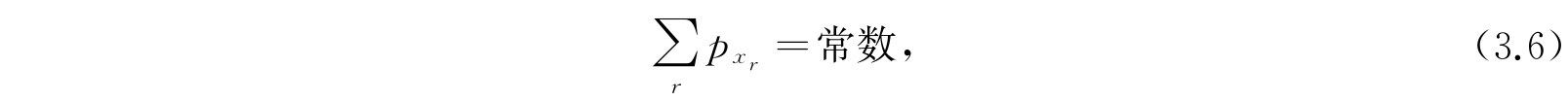
而角动量的x分量是常数，由方程
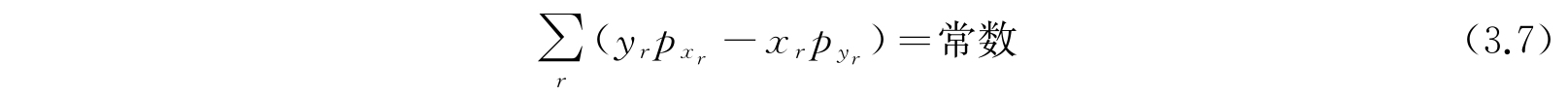
表示. 问题中的函数F是相空间中位置的一个单值（不变）函数. 这不变函数的存在把轨迹限制在相空间中一特定的曲面上，或者，如果在问题中允许这常数在一小范围内变动，这个范围是包在两个这样的邻近曲面之间；这种情况正像能量积分限制轨迹在一单个能量曲面上或在一个这样一些曲面所包的范围内.
除了能量积分以外，从这样一些外加的不变积分存在的可能性看出：当我们对于在3.4节中已讲过的关于平均的范围作选择时必须慎重. 如果这样一些不变积分存在时，它们必须明确地规定为以上所提到的一般条件的一部分. 当其他不变积分存在时，为了遵守它们所给出的附加要求，我们必须只对相空间的符合附加要求的一些区域或态求平均. 这样一些区域或态我们称之为 可及相空间或可及态 （ 或配容 ）.
但我们必须特别注意，所有关于可及性的要求是完全看实际情形而定的. 例如，对于线动量和角动量的各分量的不变积分存在的可能性通常是不加过问的，虽然我们不一定能够立刻看出其中正确的理由. 现在我们来解释这一点：任何一个现实的系集通常是被认为包围在一封皮之内的，这是具有或多或少理想性的想法，封皮本身不是系集的一部分. 封皮通常理想化到用完全反射壁来代表. 系集的体系与这个反射壁之间没有一点能量交换. 更进一步的简化是假定反射是镜面反射，也就是犹如光线从镜子上反射一样. 线动量的分量由于此系集而不保持不变了，因为任何一个垂直于壁的体系的线动量分量当这体系从壁上弹回来时就反向了，从而系集的运动方程就不允许线动量的任一分量为不变积分. 如果这理想的封皮是球形的，对于球心的角动量的各分量将不受与封皮碰撞的影响而变化，因此对于整个系集来说，这些分量也是保持不变的. 当然真实的封皮是没有这些理想性质的，因为封皮的表面在原子的大小上看来必然是粗糙的，所以体系与封皮有着能量的交换，也有线动量和角动量的交换. 当我们把封皮包括在系集之内时，那么，能量和动量的不变积分对全部系集是存在的，我们将发现在封皮和系集的其他部分能量交换的平衡条件是温度相等，由此就产生了全部热力学. 然而有关动量交换的平衡所得出的却是一个无足轻重的条件，即要求系集的不同的部分必须组成一个像刚体一样运动着的单位. 这些条件实质上没有引进任何本质上新的东西，因为我们永远可以不管一个系集的任何一部分的集团运动，而只考虑它相对于它的质心运动的内部性质，这些性质是不受集团运动影响的. 因此在任何一个热力学讨论中，线动量的不变积分和角动量的不变积分存在与不存在，对我们的研究是没有一点差别的. 如果我们认为它们是不存在的，我们可以考虑这系集是包含在一个固定的粗糙的封皮内，因而系集的所有部分必须处在和封皮相对静止的情况下. 如果我们认为这些不变积分是存在的，我们就把封皮包括在系集内；这整个系集于是必须像一个刚体一样运动. 如果它在转动，它的各部分甚至也可以与其他部分和封皮有相对运动，但是对它们进行的热力学上的研究是不受影响的. 如果这些体系形成一种气体而封皮在转动，那么，离心力将影响在气体中各处的密度分布，但是这种力的影响和通常外力的影响并无区别. 因此，我们以后就不再提及线动量和角动量的不变积分.
这里我们再顺便提到一个有趣的例子，那就是在高能核碰撞中π介子的多级生成的费米热力学理论
，其中系集的线动量和角动量问题不能同上面一样处理. 这是由于容器不存在，上面那些论据就不成立，因而我们在这个理论中就必须注意线动量和角动量的守恒.
人们也许可以预期其他的不变积分对于经典系集是可能的，但是直到现在我们还没有找到一个其他的不变积分. 所以人们也只能作这样一个结论：对于经典系集而言，受能量条件支配的全部相空间一般说来是可及的，因而在平均的过程中必须注意到这部分相空间的每一点.
然而在作出这样的结论时，我们多少是有些草率的，例如我们就没有考虑 暂时平衡 和 亚稳平衡 存在的可能性，而这些暂时平衡和亚稳平衡都是具有很大实际意义的，因此，作为关于可及性的更细致的分析就要把它们包括在内. 我们已经在事实上假定了在可及相空间，当时间处在一次观察或进行一次实验的时间数量级大小情况下，所有各部分之间具有 有效的 自由往来. 这“有效的”限制在这里具有实质上的重要性. 很容易想象，有这样一种情况，即在一次观察的时间内，代表点将不会盖住全部的可及相空间，而代表点在来回运动中它只盖住了可及相空间中某些选定区域；尽管当 给定一足够长时间 代表点实际上可以遮盖住所有可及相空间. 这就是说，当时间的数量级是一次实验的大小时，代表点实际上是被限制在相空间的特殊区域. 仅仅这一部分相空间才应当被认为是可及的，代表点只是完全盖住这些限定的领域. 我们可以举一个简单的例子：在室温下的氧和氢的气状混合物是一种亚稳平衡，真正的平衡态相应于混合气体几乎全部转换为水蒸气或水. 然而在室温下引导氢分子和氧分子转换为水分子的过程是极端稀有的，而氢和氧分子的初始数目在普通的实验时间内并不改变. 事实上，这些初始数目就是这系集的全部运动方程的有效不变积分，而可及相空间实际上是限于这样一些区域，在这些区域内这些数目实际上是维持初值的. 虽然这亚稳平衡涉及包含水的形成的变化，但在其他方面它却是很正常的，所有热力学和统计力学的计算方法都可以用来计算它的性质.
这几点都是大家所熟知的，以至我们常常忽视了它们的重要性而强调得不够. 重要的是了解到即使对于经典系集来说，每一级亚稳度都可能出现. 在上面所引用的例子中，对可及相空间的限制，实际上在较长时间的间隔内是完全适用的. 而在另外一些例子中，限制实际上仅仅在有限的时间内可以保持，因而只是一些不完全的限制. 在这种情形下，热力学和统计力学只能近似地应用. 要严格地应用它们，人们永远必须能建立可及性的正确规则. 相空间的某些区域是完全可及的，而另外某些区域是完全不可及的. 事实上，这就意味着我们必须能够说：关于可及性的说法是随问题的具体条件而变的. 用微观过程的观点，这就意味着我们必须把所有变化速率置放于两类的这一类或另一类之中，即：有一些是这样的慢，以致它们的效应在一次实验时间能够忽略，而另外一些是这样的快，以致它们能够使得系集的代表点实际上有效地盖住了表现出可及性的全部相空间. 当中间速率出现时，热力学和统计力学就不能应用了. 这些结论从经典相空间的语言译成量子态的语言是简单的，而且我们可以不在这一点上花时间.
我们强调这几点的原因是，对它们真正的了解使得由量子论引进的可及性的新条件出现得更加自然些. 量子力学的更加细致的讨论已经指出一个由相似体系组成的系集并不是所有态从一个态到另一个态都是可及的. 利用这些态的对称性可以把它们分为若干群无联系的态. 任一适当指定的态的对称类型是一个绝对运动常数，等价于经典名词中一个真正的不变积分. 符合在3.4节中所指出的，关于求平均所要求的这组可及态，是一组在特定的能量范围内，具有正确对称性质的态.