下载掌阅APP，畅读海量书库
立即打开
直到现在我们已经取消了对经典力学以及与它有关的一切的信赖，因为我们知道，经典力学在原则上是不能应用到原子系集上去的，而且只有在适当的极限情形下才给出正确的结果. 但在这里来描述一个遵守经典力学的系集，并且研究在经典力学中可及性的条件是很合适的，因为这些描述和研究很自然地引导到在量子理论中所设置的可及性的某些更加微妙的条件.
一个遵从经典力学定律的系集，当它的能量作为N′个广义坐标以及与它们相适应的N′个广义动量的函数是已给定的时候，它就被完全描述出来. 如果支配系集的外力场是保守的，那么系集的能量可以用哈密顿的形式H（x，p
x
）写出，这里x是N′个坐标x
1
，x
2
，…，x
N′
的简写，而p
x
是其相应的动量
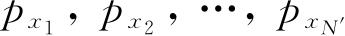的简写. 在这种情形下，H中再也没有其他变量. 如果系集不是处在保守力场中，例如，假如间壁和在系集外的其他物体是用一些和在H中出现的x不同的坐标来描述的，这些坐标本身是时间的函数，那么这个与时间有关的部分可以从H中取出而在以后作为微扰引进来. 我们暂时忽略这些与时间有关的力，然而应该想到，在原则上它们永远不能从任何一个真实的系集中省去. 对于在一保守力场中的理想的系集的经典哈密顿运动方程是
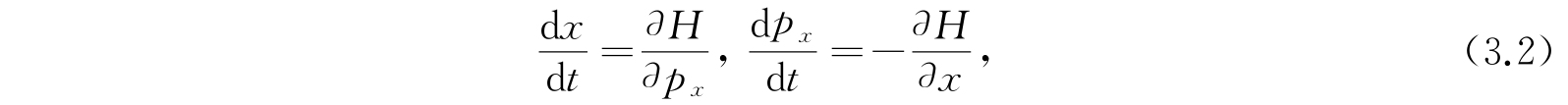
总共有2N个方程. 坐标x可以是任何一组能够充分描述在任何时刻系集的几何位形的量. 例如，对于一组含N个每一质量为m的无结构的粒子系集，一组天然的坐标将是N个粒子的3N个笛卡儿坐标：
x α ，y α ，z α （α=1，2，…，N），
因此相应的动量（术语上称为共轭动量）是下列3N个变量：
由方程（3.2），我们可以导出
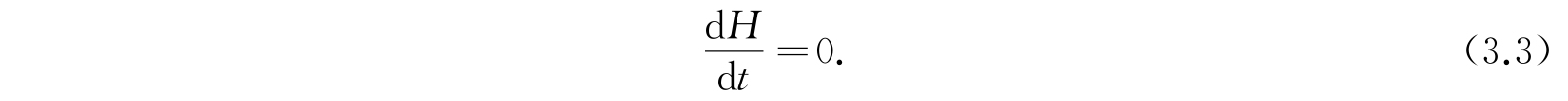
它告诉我们能量不随时间变化，我们能把方程（3.3）写成积分形式
H（x，p x ）=E， （3.4）
这里E是一个常数. 一般说来，一个由所有2N′个变量x、p x 或其中一些变量确定的单值函数，在系集的全部运动中为常数，那么，这样的关系被称为运动方程的 不变积分 . 所以方程（3.3）告诉我们，能量是运动方程的一个不变积分.
当所有的坐标x和动量p x 作为时间的函数是已知时，经典系集的全部行为就知道了，这就提出了系集的经典情形的几何表象，它们将有助于任何一般性的讨论. 当所有的x和p x 都已知时，在任一时刻系集的态就完全已知了，我们用2N′（=6N）维空间的一点来代表系集的态，而用x和p x 作为这点的笛卡儿坐标，这个空间为 系集的相空间 ，而相空间中的点所划出的路径为它的 轨迹 . 这轨迹遵守系集的运动方程（3.2），而且对于保守系集，此轨迹可以由这些方程和它的起始点完全决定. 一个确定的保守系集的两条轨迹是永远不能相交的，否则如果取这样一个假设的相交点作为起始点，那么在此点出发的解将不是唯一的，这就引到矛盾的结果. 另外任何一条轨迹都被限制在相空间中由方程（3.4）所决定的超曲面上运动. 当非保守的微扰作用时，相当的附加项必须包括在这些方程中，因而受扰动的轨迹自然更要复杂得多. 可以认为，过了或长或短的时间以后，轨迹可以接近一族或另一族未受扰动的轨迹，我们可以这样来看：包围在两个邻近的、能量间隔dE不太宽的能量曲面之间的相空间是微扰运动的相空间，在微扰作用下，系集将走遍这微扰相空间中所有的点，并且不时地慢慢地由这一族中的一轨迹过渡到其他的轨迹上去. 这族轨迹可以这样来决定，即：它们是一些保守的适当系集的准确轨迹，而这个系集接近于真正受扰动的系集.
对我们而言，经典系集的讨论价值在于 极限原理 上，即：经典系集永远可以当作相应的量子系集的极限形式. 为了能够用经典定理来说明相应的真实的量子情形，就必须了解如何把量子理论的间断的本征态和在经典相空间中相应的点的连续变化的态在分布上进行比较. 很幸运的是，这个问题人们早已给出了完全答复，那就是对于一个N′自由度的系集，每一个满足特定的边界条件和系集的薛定谔方程的不同的本征函数，它所代表的态占据经典相空间的一个等于h N′ 的区域. 这种对应关系一开始就使人联想到它作为玻尔对应原理的一部分，是一条对于大的量子数正确成立的普遍定理. 我们将在下面一章从几个简单的事实中作一些直接估计的验证. 在这之前，我们将把每一量子态和相空间一个等于h N′ 的区域相对应的关系，作为一个事实采纳下来.