下载掌阅APP，畅读海量书库
立即打开
由上一节可以看到，我们必须要对态进行选择. 态的选择直到现在还不能建立在一种由因到果的完全严格的论证基础上，态的选择法可以有很多种，很幸运的是：当它们用到大系集时，所有这些方法都得到同样的物理结果. 这里我们不打算叙述这些选择法，也不打算叙述那些使得这些选择法似乎有道理的理论背景，而是立刻把必需的基本假说的说法用公式表示出来，这种说法是在我们其余部分的讨论中将要采用的. 关于基本假设的任何一种说法的最后验证是在应用中不出毛病. 因此，这里我们从若干可以互相代替的假说中采取下面的一种：
罗列出相应于一特定的能量，或一特定的能量间隔以及相应于任何其他给定的一般条件的系集的所有各种不同的态
.
我们可以算出系集的任一性质
Q
的平均值
，
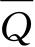这个平均值给出了遵守一些特定条件的系集的平衡态，在求所有这些态的平均值时，其中每一态的权重都相等（等于
1）. 形式上可以写成
这种说法仍然有些含糊，并且将进一步被改善.
为了平均过程的需要，我们已经选择了给定能量的态. 这看起来是很自然的，甚至不需进一步分析，因为我们想象的系集是被认为具有一定的或近似一定的能量的，因此在这样一种情形下，其他不等于这能量的态的性质很难看出是有关的. 但是人们可以这样地问：是否已经再也没有同样重要系集的原子变量的其他函数？它的不变性可以组成上面平均规则的说明中已提到过的其他一般条件的一部分？关于这样的函数的研究，引导到我们对某些态能不能出现的问题，也就是态的 可及性 的问题. 在能够给出平均规则的明确规定之前，必须把这个概念明确起来，这是下面几节的任务.