下载掌阅APP，畅读海量书库
立即打开
在前节中我们看到，虽然在原则上分子的结构和能态可以用量子力学计算，而实际上只有最简单的问题；如类氢原子才能够准确地解出来. 甚至于相当简单的双原子分子也需要用近似的核间势；因此多原子分子的理论计算几乎是不可能的，幸而对我们在以后的计算来说，有粗略的近似已经足够. 因为各种原子核的体积是这样的小，常常可以把核看作质点. 那么多原子分子中核的相对运动是由各种振动方式组成的. 在这一粗略近似中，我们将认为每一种振型是一个谐振子，而忽略非谐性. 一旦给定了各种基频，如2.4节所述，就很容易计算能级的分布. 我们也忽略转动和振动间的相互作用，也就是把转动考虑成刚体的.
假如分子是线性的，转动态就已经在2.15节中讨论过了. 若分子是非线性的，但有这样的对称轴使得绕对称轴的转动惯量是C，而绕另两个通过重心垂直对称轴的转动惯量都是A，则分子就是一个对称陀螺. 对这样一个对称陀螺，转动能级已计算出来（可参看量子力学的书籍），
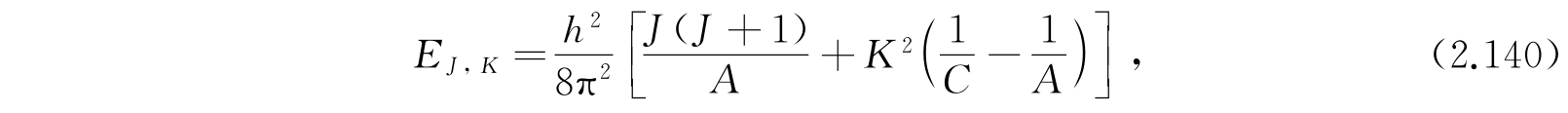
其中J是总的转动量子数. Kh/2π是角动量沿陀螺对称轴的分量. 除这些量子数外，还有另一个量子数M；Mh/2π给出沿任意固定在空间中的轴的分量. 这些量子数可能取的值是
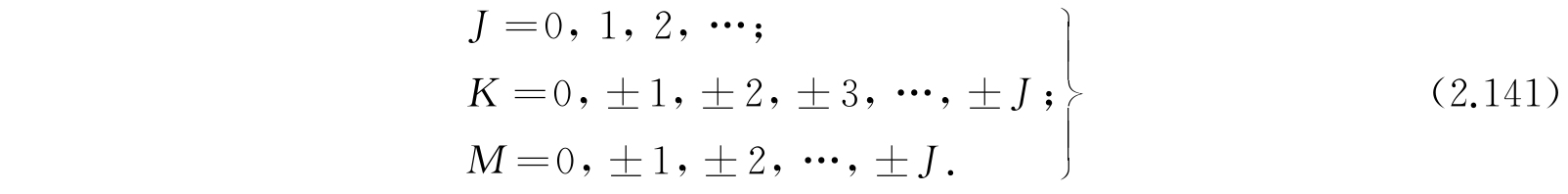
当K是零，E的表示式就化为线转子的表示式. 于是能量与M无关，也不依赖K的符号，因此对给定J的能级退化次数是2J+1或4J+2，视K是否等于零而定. 当分子的结构已知，A和C就可以由原子核的质量算出.
多原子分子的振动频率可由红外光谱测定. 若n是分子中原子的数目，每一个原子有三个自由度，总共就有3n个自由度. 分子整体的平移运动有三个自由度. 对一个线性分子来说有两个转动自由度，对于非线性分子来说有三个转动自由度；因此对于线性分子就有3n-5个振动频率，对非线性分子有3n-6个振动频率. 但是分子中常有某些对称性，并非所有的频率都不同. 但是波动力学和数学中的群论结合以后，就能够迅速地计算出这些不同频率的数目，以及每一种振动型的多重性. 这里不再作分析，因为对于很多分子，这些数据已收集在像赫兹堡那样的著作
中. 其次对于热力学计算而言，一般来说，对多原子分子的振动作一个更粗糙的近似就已足够. 在第5章中对这点要进行解释，这一近似方法并不需要实际测定的准确的分子振动频率.