下载掌阅APP，畅读海量书库
立即打开
前一节所给出的简单处理与实验有一些不符合的地方，上节给出的是有均匀间隔的能级，而实验观察到的振动能级却显示出随v增加而收敛. 为了获得这样一个特点，就需要用比前节中的势函数更接近于真实的势函数U（r），特别要注意对大r值时势函数的行为.
莫尔斯（P.M. Morse）建议了下列形式的势函数：
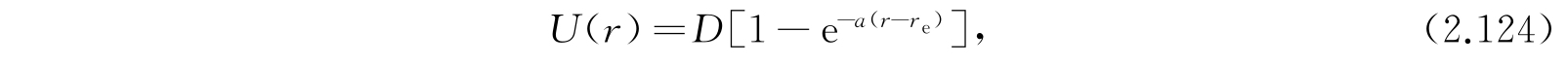
它在r=r e 处有极小值为零，对大的r值趋近于某一有限值D. 在r=0处，实际的势能函数应该是无穷大，但莫尔斯势却是有限的. 不过，莫尔斯势在这一点的值也很大，所以这一缺陷并不严重.
将式（2.124）代入式（2.110），我们得到
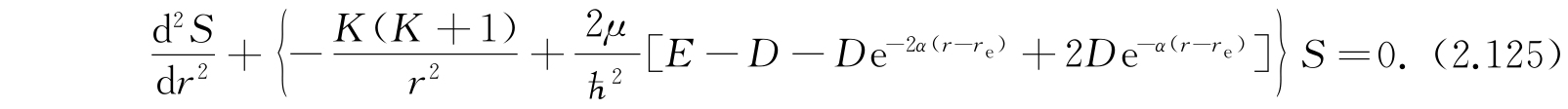
我们作下列替换：
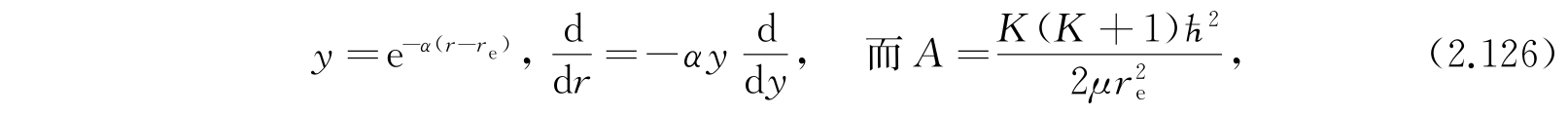
方程变为
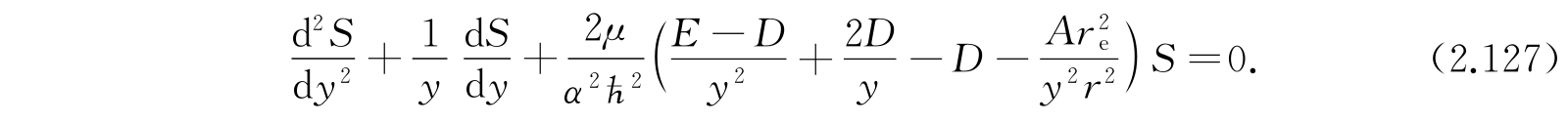
最后一项是转动和振动型的耦合效应，所以在低转动和振动态时是很小的. 在平衡时r=r e ，y=1，我们把（r e /r） 2 展成（y-1）的幂级数：
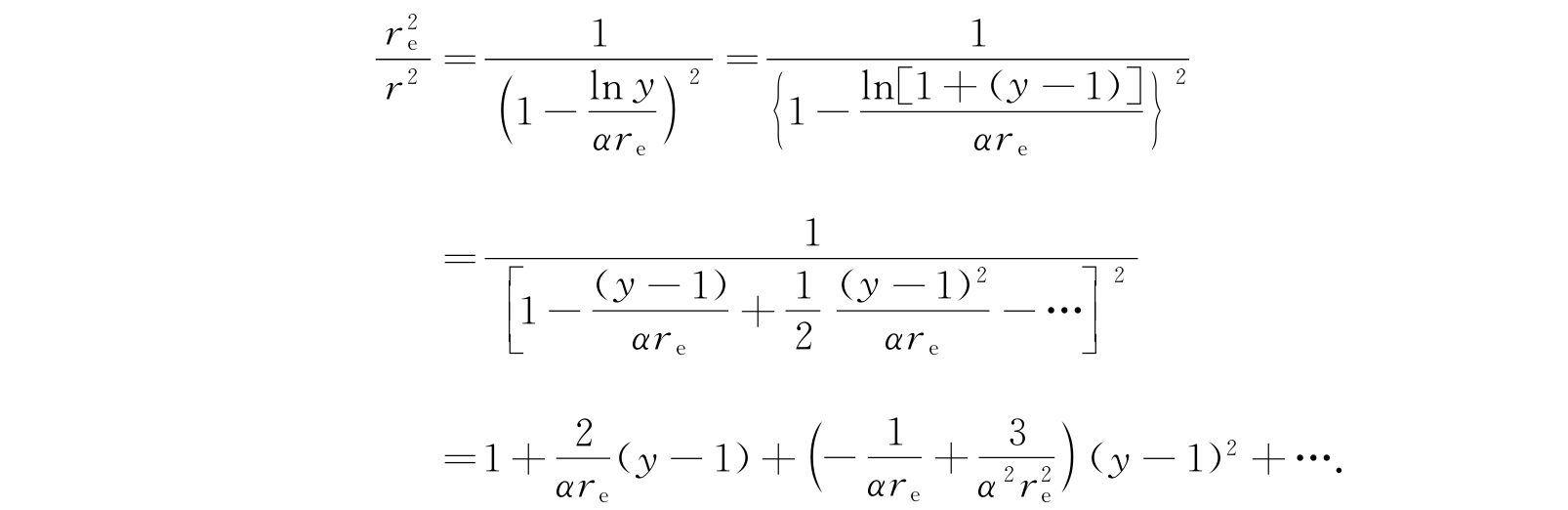
只用已经写出的前三项，方程（2.127）就变成
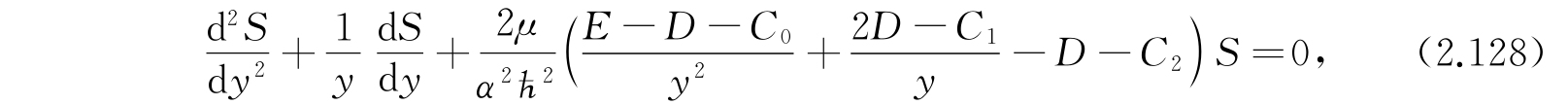
其中
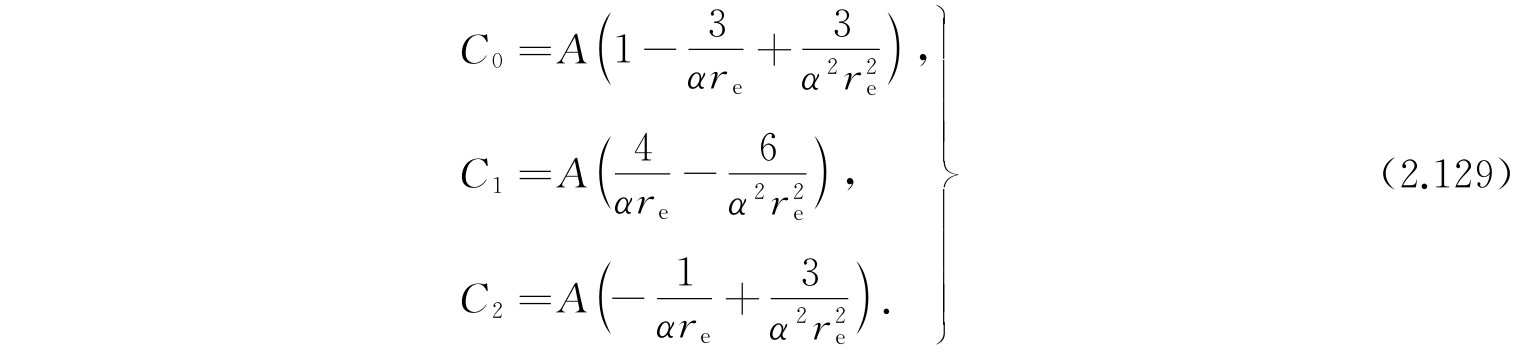
现在用下列替换可以把式（2.128）化成前面处理过的氢原子的径向函数方程：
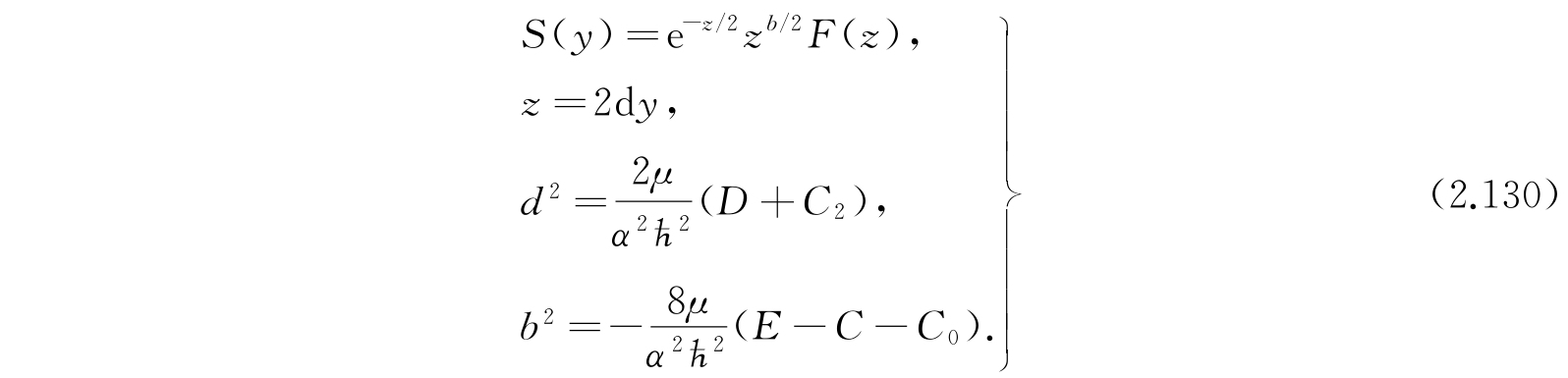
于是就有
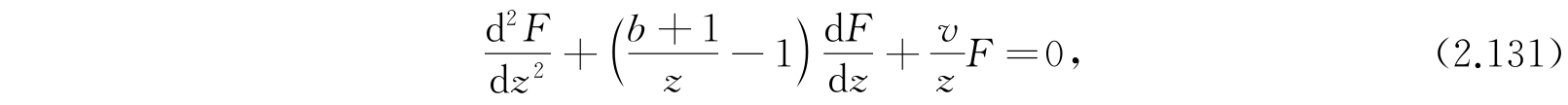
其中
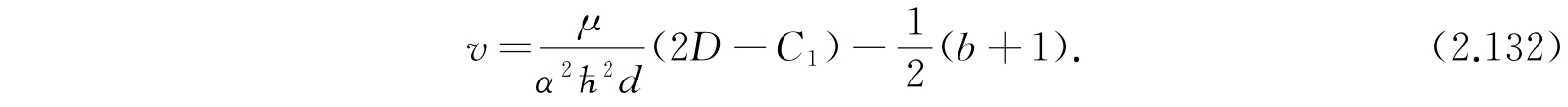
这一方程与氢原子的半径波函数的方程很相似，并且能够用拉盖尔多项式解.v的本征值是0，1，2，…. 利用式（2.130）和（2.132）解E，得
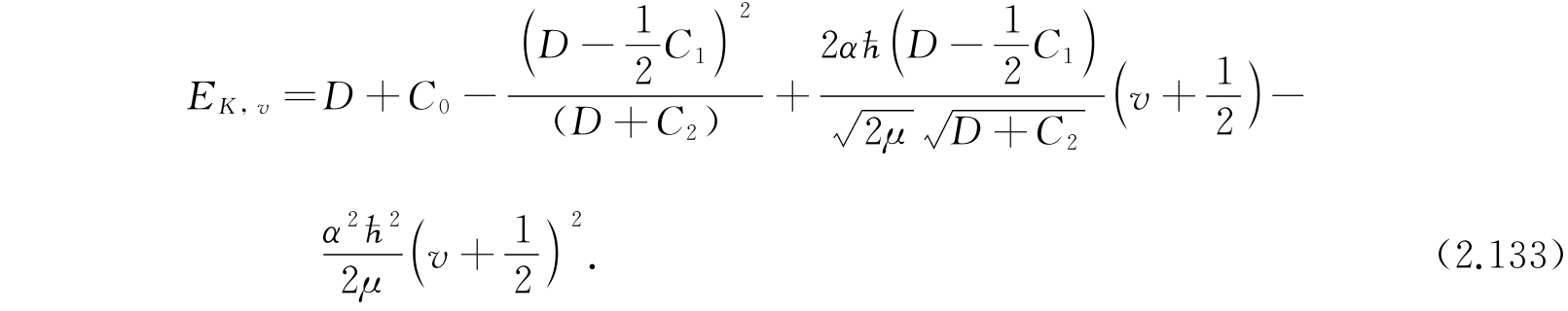
因为A是很小的，因此我们应该把上面的表示式展成C 1 /D和C 2 /D的幂次项，于是
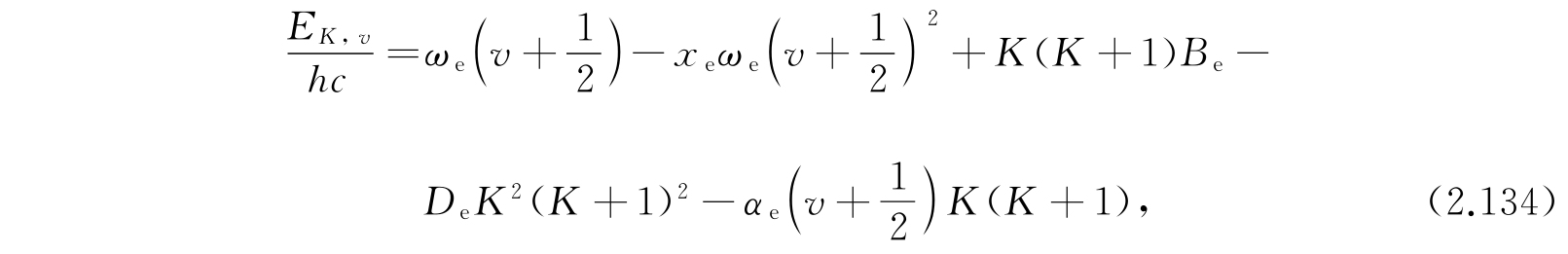
而
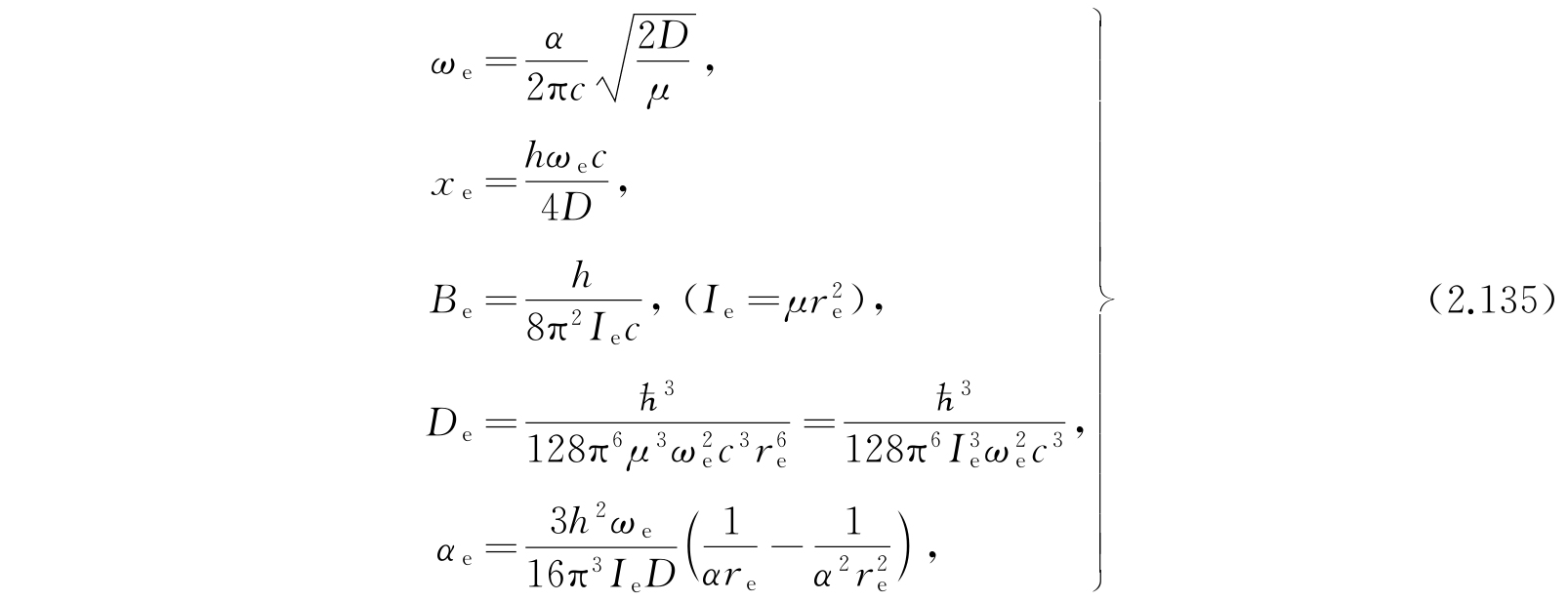
其中c是真空中的光速.
这一关系式几乎对所有双原子分子都能给出非常精确的能级数值. 无须说明，所有的计算是关于较低电子能级的. 式（2.134）中的常数的实验值曾经由赫兹堡（G. Herzberg）
给出. 根据假定的势函数V（r），显然由式（2.134）计算的E只当E<D时才有意义. 对E>D，按照2.2节的一般讨论，能级应该是连续的而不是间断的. 所以间断能级的数目是有限的. 在应用式（2.134）时必须记住这一事实. 基态（v=0，K=0）的能量是
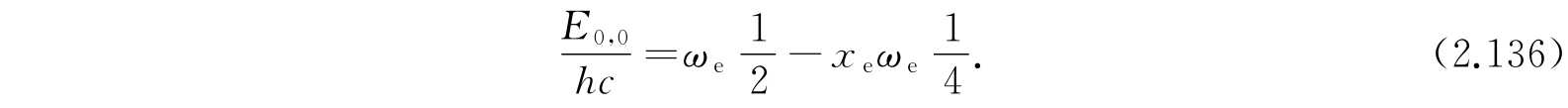
E K，v 和E 0，0 的差值是
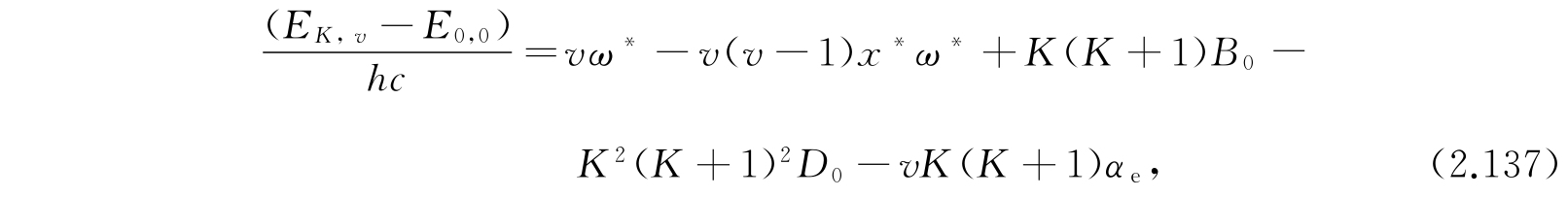
其中
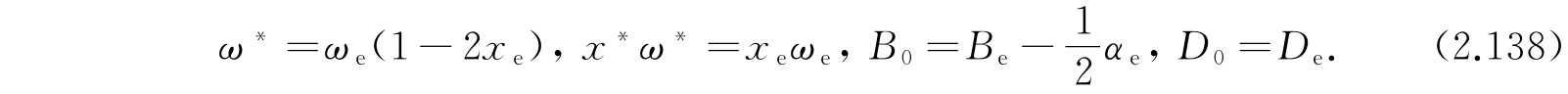
离解能是D-E 0，0 ，即
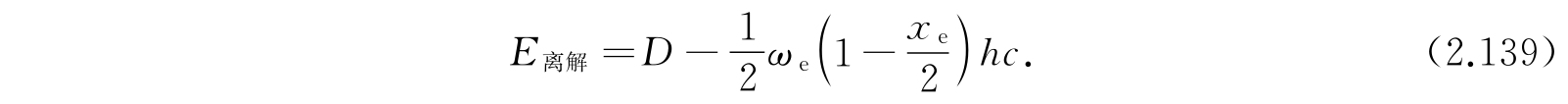
D可以按照式（2.135）由ω e 和x e 计算出来，所以离解能也可以从光谱数据计算出来. 但是式（2.135）由各种近似得到，这样测定的离解能不可能希望是准确的；实际上也常和用更直接的方法所确定的数值不很一致. 我们可以举一个例子，考虑氯化氢（HCl）分子，就有
实验值是102.1 kcal/mol（1 cal=4.186 8 J），约有17%的误差，但作为估计则是够用的了. 这说明从光谱的数据，我们能估计分子的离解能.