下载掌阅APP，畅读海量书库
立即打开
关于双原子分子的原子间的力能够作出的最简单的假定是：力正比于核间距r和它的平衡值r e 的差值. 因为U在r e 处有一极小，从而在r e 附近，
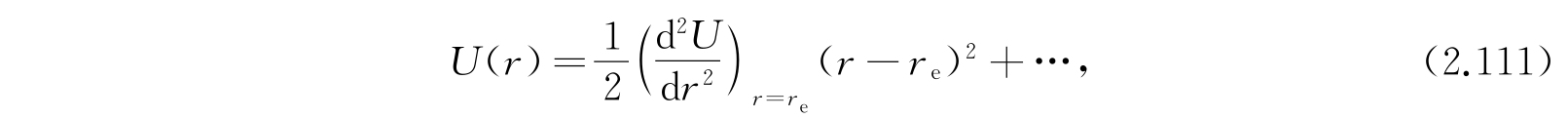
在r e 处U取作零，所以能量W是从U（r e ）量起的. 令
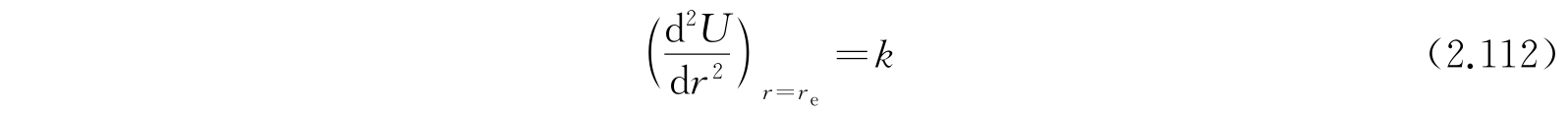
和
ρ=r-r e ， （2.113）
由方程（2.110）得到
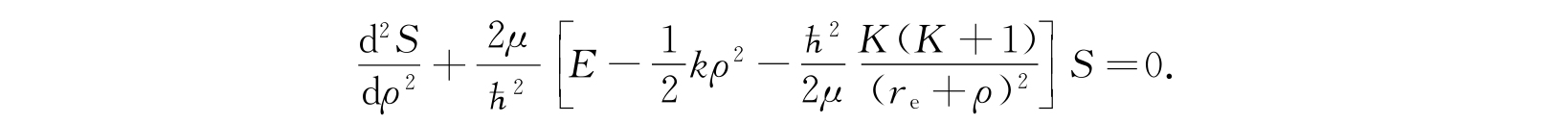
由于这一近似只对小ρ值适用，因此上述方程中最后一项应该展成
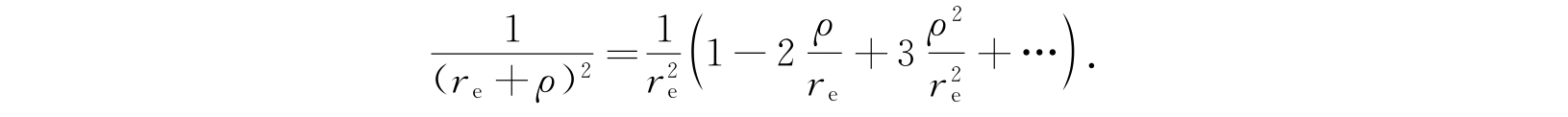
保留到ρ的平方项，方程可以写作
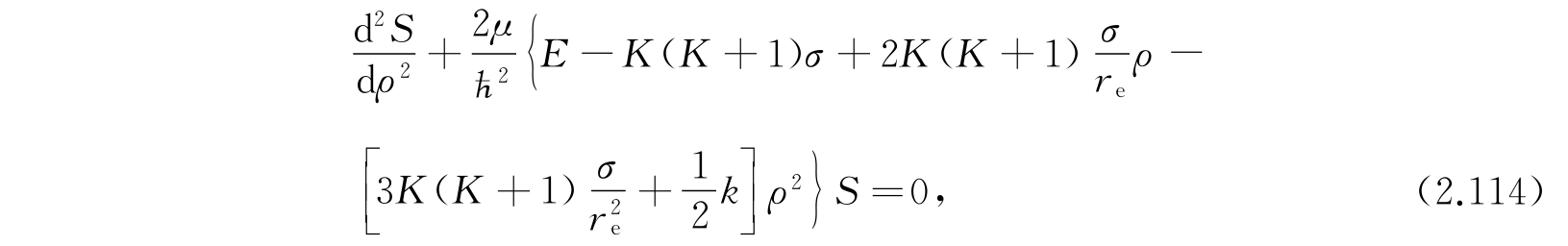
其中
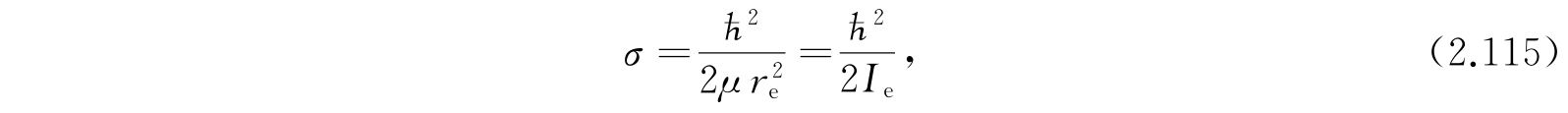
I e 是分子转动惯量的平衡值.
利用
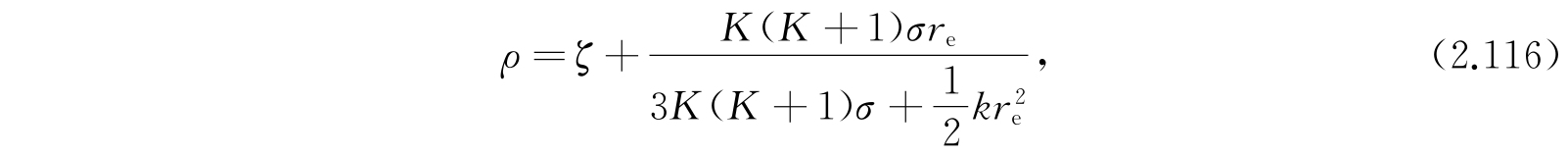
我们能够把式（2.114）化为式（2.25）那样的谐振子方程：
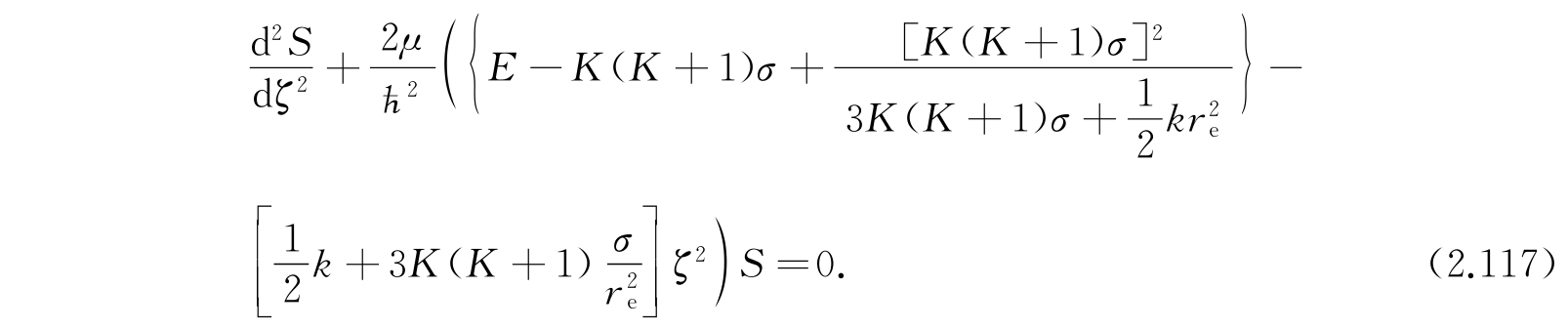
边界条件是在r=0和r=∞时S等于零. 这一条件和谐振子的边界条件有些不同：对谐振子在ζ=±∞时S是零. 但是因为S在经典许可的区域以外迅速地减少，把这两个条件看作等价，实际上也并不会引进严重的误差，所以我们可以用谐振子的波函数作为函数S的近似.
于是能级为
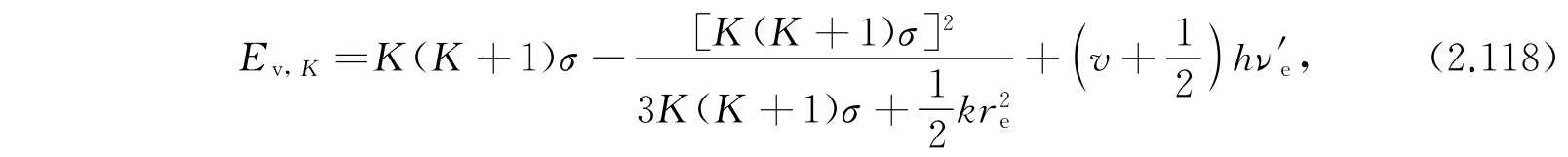
其中
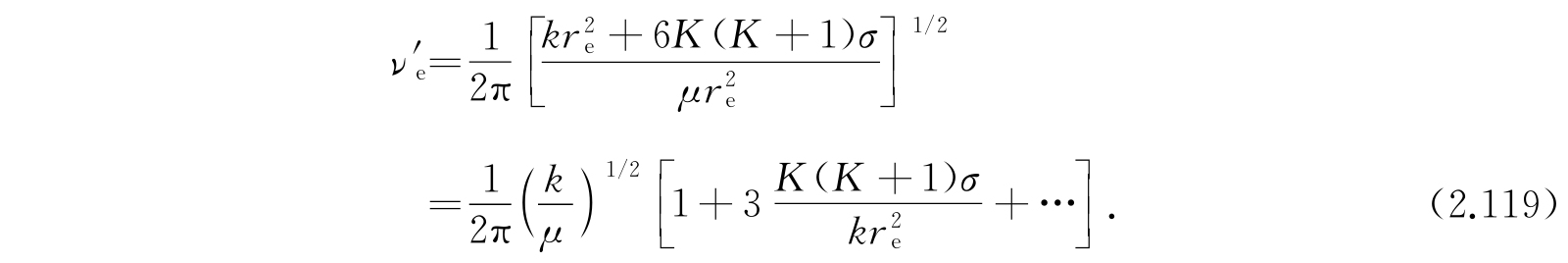
如果我们引入在平衡状态附近的振动频率ν e ，
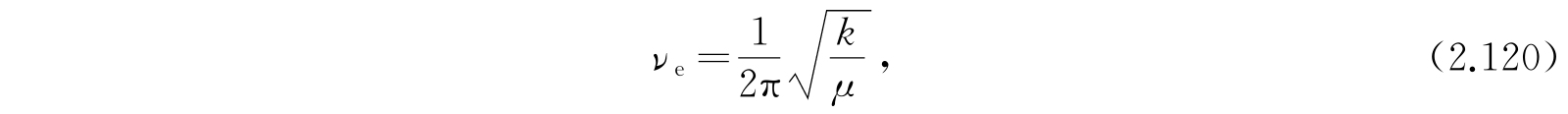
就得到最终的近似公式
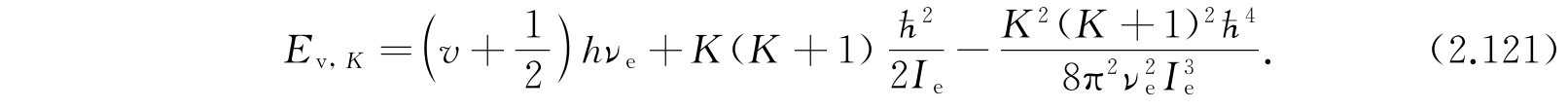
第一项显然是分子被看作谐振子的振动能；第二项是假定分子为刚体时的转动能；第三项的来源是：考虑非刚性分子由于转动产生分子的伸长，伸长后角惯量又有所改变，因此又产生这个修正项. 更高次的项并不可靠，因为所假定的势函数不够精确. 大多数分子的实验数据很好地适合方程（2.121）. 对于更精确的工作，还需要其他的项并且需要比式（2.111）更精确的势函数.
前面已经说过，量子数K是和分子的转动关联的. 但是现在得到的转动能是
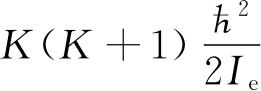. 若p
θ
是转动的角动量，就正如线性动量的情形，转动能是
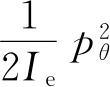. 所以对任何特殊K值，角动量是
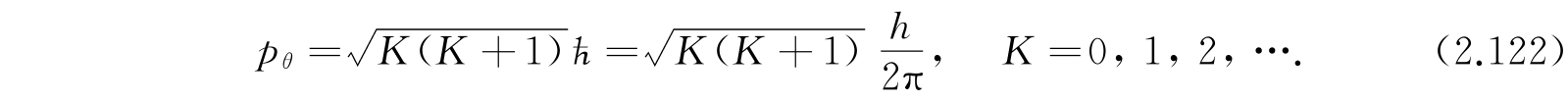
因为按照方程（2.107），有2K+1个M值与各个不同的波函数对应，也与不同的转动轴定向对应，所以转动态是2K+1重退化的. 事实上发现在任意特别选定的方向，例如分子的轴（取作z轴）上角动量的分量是
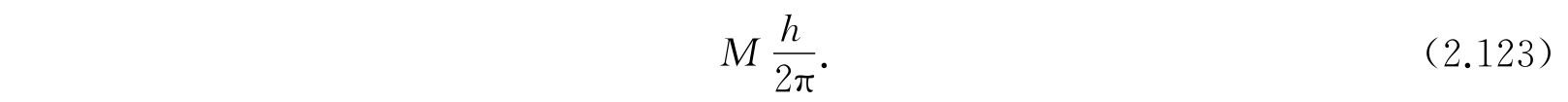
这些结果对任何具有转动惯量为I e 的刚性线转子都是对的. 需要着重指出的是：按照方程（2.115），决定I e 的是平衡核间距和核质量，而不是原子的质量.