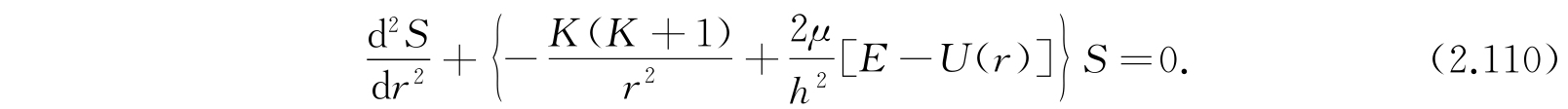下载掌阅APP，畅读海量书库
立即打开
现在我们要考虑最简单的分子——双原子分子的原子核波函数和对应的能级. 我们将假定第n个电子能量U n 现在仅是核间距离r的已知函数. 双原子分子的振动-转动波函数ψ n，v 适合
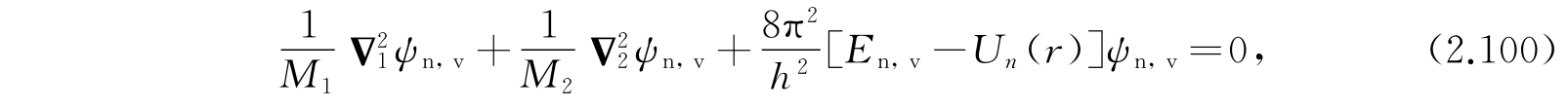
其中ψ n，v =ψ n，v （x 1 ，y 1 ，z 1 ，x 2 ，y 2 ，z 2 ）是核运动的波函数，M 1 和M 2 是两个核各自的质量，而
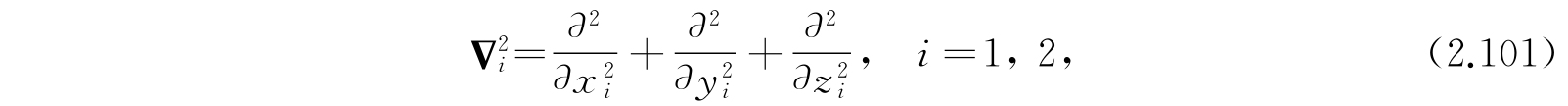
x i 、y i 、z i 是第i个核相对于固定在空间中的轴的笛卡儿坐标. 方程（2.100）与氢原子的波动方程一致，不过这里的两个粒子都是原子核而不是一个质子和一个电子. 所以在处理这一方程时可以和前面的氢原子方程联系起来（参看2.6和2.8节）. 在U n （r）的形式中代入r的方程以前，所有的步骤是相同的. 因此，分子的内部运动的方程变成
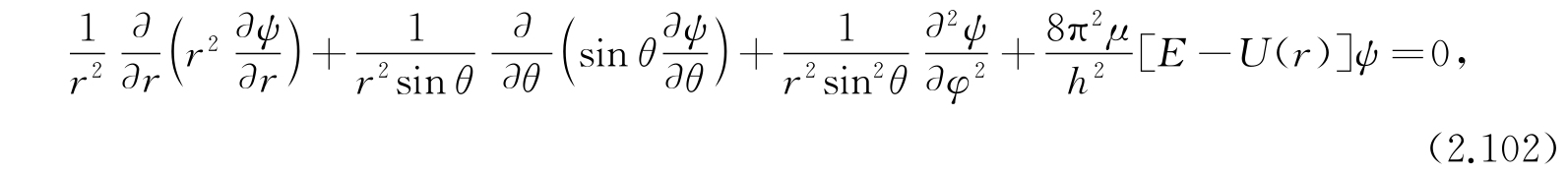
其中μ是约化质量，
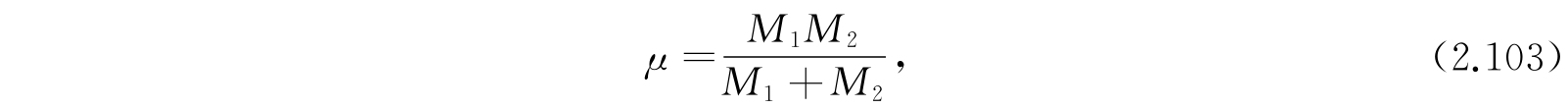
而r、θ、φ是第二个核相对于作为原点的第一个核的极坐标. 假若我们设
ψ（r，θ，φ）=R（r）Θ（θ）Φ（φ）， （2.104）
如同对类氢原子一样，我们有
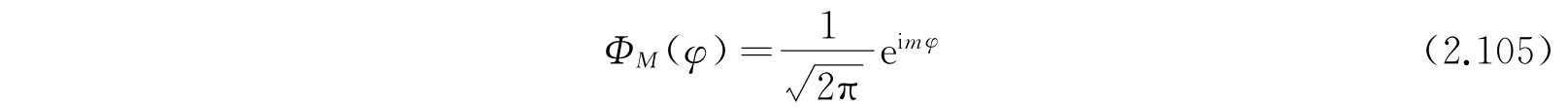
和
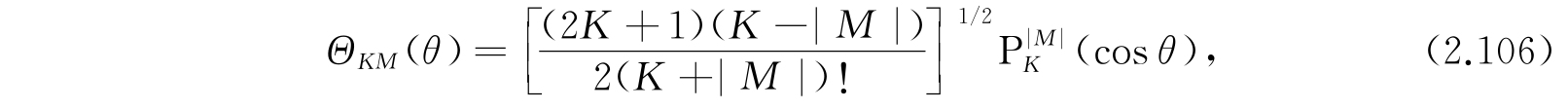
其中
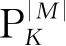（cos θ）是一个关联勒让德函数. 按照分子光谱学家的习惯，K称为角量子数，M称为磁量子数.K与M都必须是整数，并且
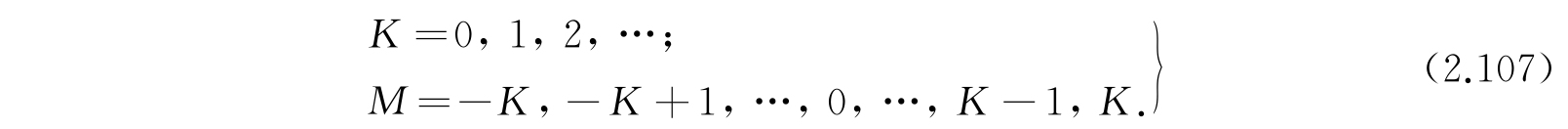
正如氢原子的情形，量子数M和K代表角动量.
R（r）的方程是
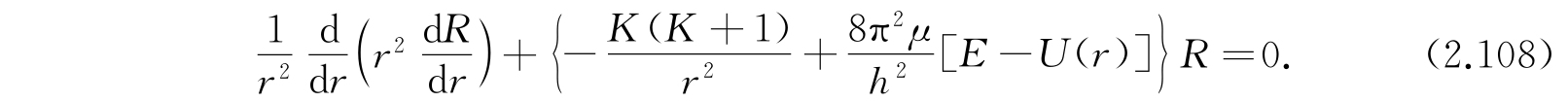
利用替换
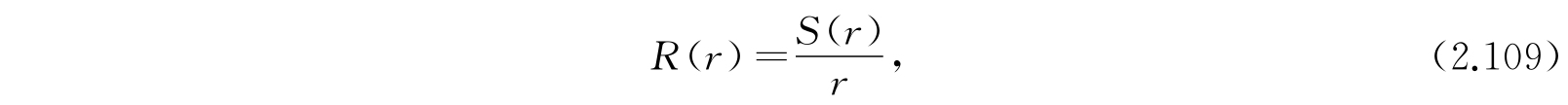
我们有
