2.12　分子的波动方程

按照2.5节，可以立刻写出分子的不包含时间的薛定谔方程

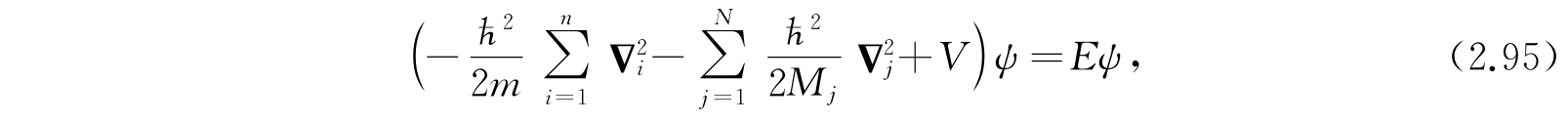
其中包括n个电子和N个原子核，而V是各对静电作用势能的总和. M _j 是第j个核的质量，E是总能量. 如果以方程（2.94）所表示的量为基准，那么很显然，核的动能将是一个四级项. 假使把这略去，波函数ψ中包含的核坐标R _j 就仅仅作为参数，而方程（2.95）是以r _i 为坐标的、描述电子运动的波动方程，原子核固定在R _j . 在这一情形中，电子波函数 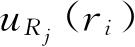和能量U（R _j ）对应. 把U（R _j ）看作势函数可以得到核运动的方程，并且利用它可以得到核的波函数w（R _j ）.

我们把ψ写成下列形式：

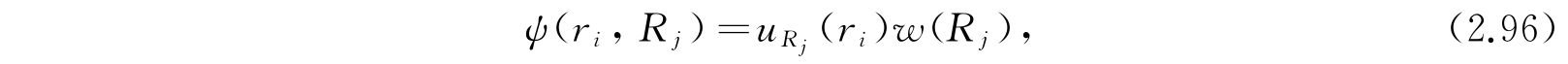
其中u满足方程

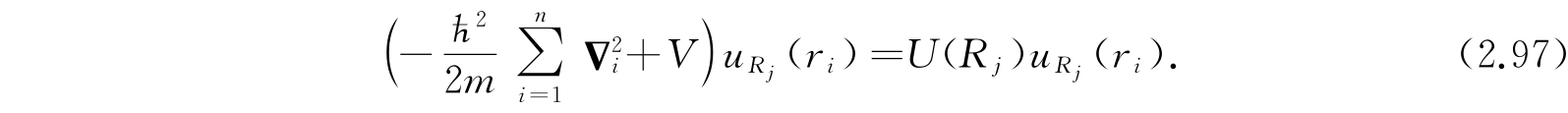
对每一种核的排列，U（R _j ）作为方程（2.97）的本征值来求得. 一般地，与分子的不同电子态对应可以有几个解；必须注意保证u和U随R _j 连续地改变，特别是在体系退化的时候更加要注意. 将方程（2.97）乘以w（R _j ），则由于算符 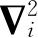对w（R _j ）不起作用，我们得到

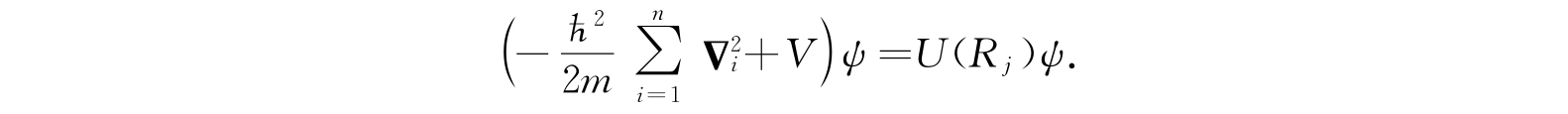
由方程（2.95）减去这一方程，我们就有

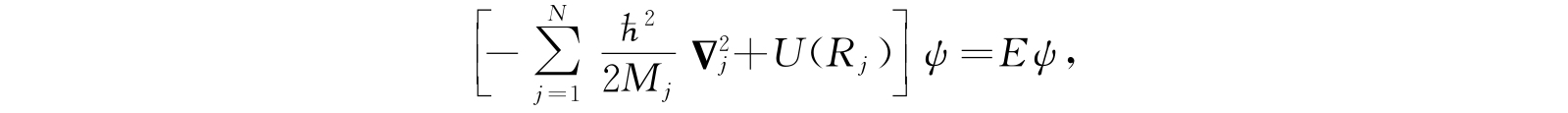
这可以重新写成

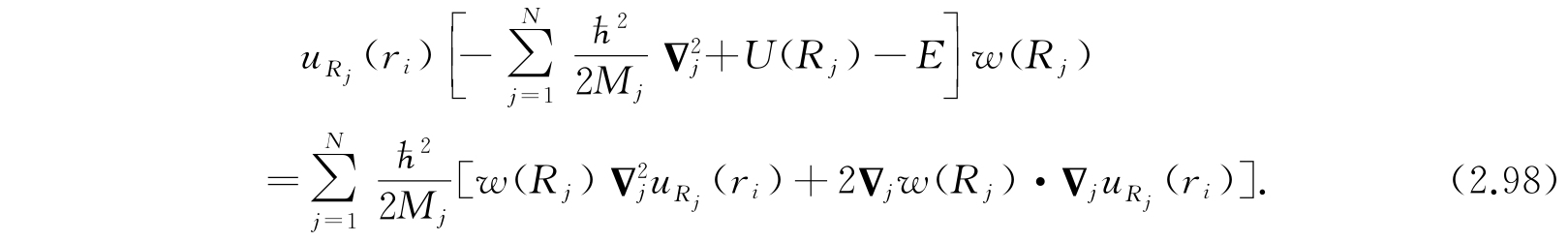
但是我们在前面已经论证过，电子运动的振幅比原子核运动的振幅大得多，也就是方程（2.94）的参数是很小的. 在这种情况下，电子的运动范围把整个原子核的组织包括在内，不会对细微的各个核位置变化有敏感，也就是说，电子波函数 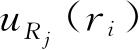不能强烈地依赖R _j ，所以 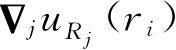是小量. 于是方程（2.98）的右方全是小量并可以略去. 所以

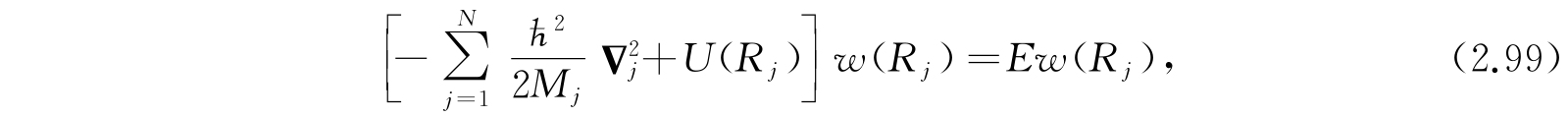
这是原子核运动的近似波动方程. MS3BcZ7bKHqWswj/L7S220I5P1clAocMcYpk9JvA4q3RTEkBbXaqZ9OfGOLkNc1B