下载掌阅APP，畅读海量书库
立即打开
原子核质量比电子质量大很多，这一简单特点是各种分子的近似处理法的基础. 这隐示了与核运动联系的能量比电子绕核运动的能量要小得多. 因为运动周期的数量级是ћ
被能量除，故分子中原子核的运动周期也就比电子周期长得多. 因此在计算电子运动时，可以把核看作固定不动；而且在计算核运动时可以假定对每一瞬间的核布置，电子都有相应那么一个核布置的自己的定常运动；也就是电子运动能够及时地适应核位形的变化.
分子中原子核要求有一个介乎完全松散和完全密集的结构之间的稳定平衡的布置. 完全松散的结构是不稳定的，根本不能形成分子；完全密集的结构也是不稳定的，因为原子核荷正电，在短距时会互相排斥. 原子核的运动可以分为平移、以平衡布置整体的刚体般的转动，以及各原子核在平衡位置邻近的振动即分子的内部振动. 如原子一样，平移运动和自由粒子的平移相同，没有非经典的运动特点.
因此，我们可以把分子的能级分成电子能级、振动能级和转动能级三种形式，我们可以估计这些能级的相对数量级. 假定分子的线性尺度的数量级为a. 与价电子（它运动时几乎扫过全部分子容积，而不是约束在近核的内层）的运动联系的能量数量级与一个在半径为a的圆轨道上运动的、质量为m的电子的能量同级，也就是
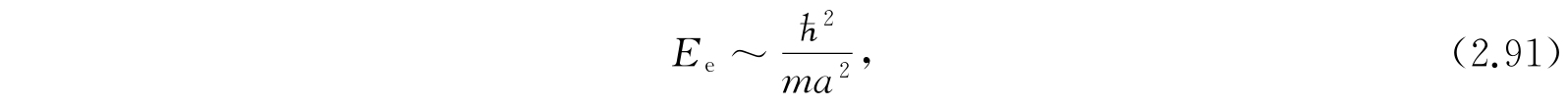
当a的数量级是几个埃的情况，这个能量相当于可见与紫外光谱区的跃迁频率.
为了估计振动能，我们把每一种简正振动型看作质量为M和弹性系数为K 0 的谐振子.M和典型的核质量同级.K 0 可以这样估计，沿一简正振动型位移一分子尺度a那样大的距离，一定会产生数量级相当于E e 的能量变化，因为这样大的位移一定会引起电子波动的畸变；因此我们令K 0 ～E e /a 2 . 于是与一个低能振型联系的能量是
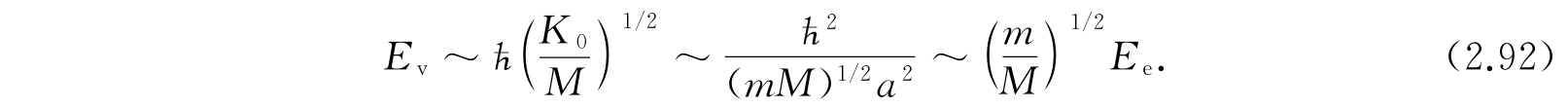
取M是五个质子的质量，那么M/m～10 4 . E v 差不多比E e 小一百倍，与近红外区的跃迁相当.
转动能E r 可以用分子的转动惯量J（～Ma 2 ）来估计. 低能转动型的能量数量级为ћ 2 /J，我们有
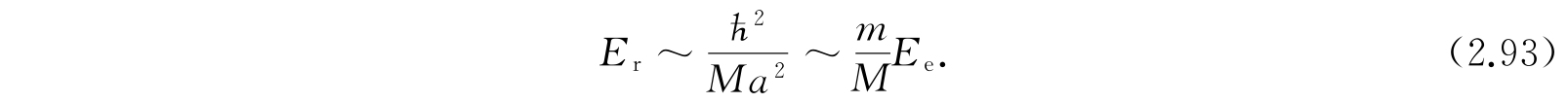
这差不多又比E v 小一百倍，与远红外区的跃迁相当.
由方程（2.92）和（2.93）可以预料到：电子能级、振动能级和转动能级可以看作是基于小比率
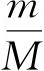（它通常在10
-4
~10
-3
范围里）的展开式中相继高次的项. 这实际上就是玻恩和奥本海默（Oppenheimer）
的处理方法. 他们用典型的核振动位移和核间距离（数量级是a）的比例作为展开参数. 能量为E
v
和弹性系数为K
0
的振子位移的数量级为
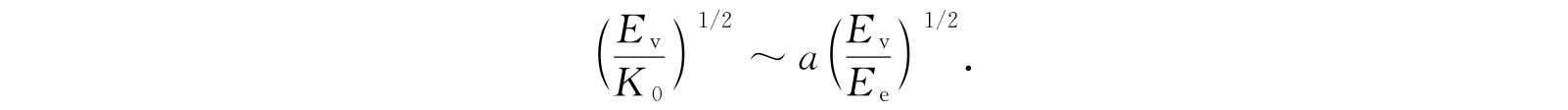
所以展开参数为
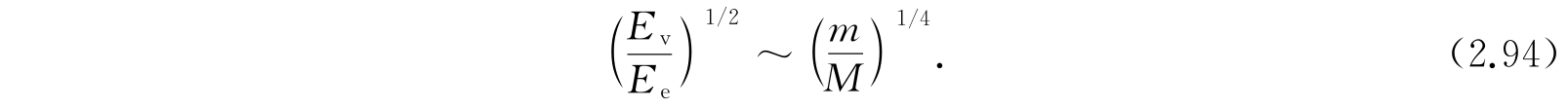
用术语来说，电子能级是零级项，振动能级是二级项，而转动能级是四级项；相应于第一级和第三级能量的运动并不存在，也就没有第一级和第三级的能量.