




在前几节中,我们处理了类氢原子并给出能级的完整描述. 现在出现的基本问题是:在多电子原子中,核外电子如何配布?我们由基本原理知道某些条件限制了可能的电子状态数目. 到现在为止,我们讨论过三个量子数n、l和m,但这还不足以完全地描写一个电子的行为. 除了这些数量外,电子还具有表示式为
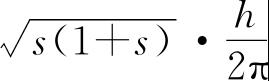 的角动量,与这相联系的有一个磁矩. 这一性质通常称为电子自旋,它是乌伦贝克(Uhlenbeck)和古德斯米特(Goudsmit)为了解释原子光谱线的多重分裂现象所引进的假定. 上述表示式中的参数s被称为自旋量子数,它只能有
的角动量,与这相联系的有一个磁矩. 这一性质通常称为电子自旋,它是乌伦贝克(Uhlenbeck)和古德斯米特(Goudsmit)为了解释原子光谱线的多重分裂现象所引进的假定. 上述表示式中的参数s被称为自旋量子数,它只能有
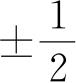 的数值.
的数值.
由薛定谔方程不能推出电子自旋现象是这一处理的缺点. 狄拉克(Dirac)的相对论量子力学,虽然到现在只能用来讨论单个原点,但却能导出结论:粒子的状态由四个量子数描述,其中之一是自旋量子数.
自旋量子数的两个数值可以看作是自旋角动量相对于轨道角动量的两种可能取向. 在原子中任意两个电子,有相同的自旋量子数就被认为自旋的方向是平行的. 如果两个电子的自旋量子数不同,也就是
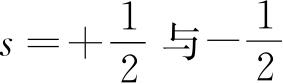 ,则自旋是反平行的.
,则自旋是反平行的.
明确了描述电子状态的四个量子数n、l、m和s以后,我们回到多电子原子的可能电子态问题上来. 泡利(Pauli)的不相容原理指出,同一原子中,没有两个电子能有完全相同的四个量子数. 假使原子中的两个电子有相同的n、l、m,它们的自旋必然是反平行的. 利用这一原理可以构成多电子原子中电子在各种状态上的配布. 我们不再在这里像物理或化学的教科书那样作详细的讨论.