
下载掌阅APP,畅读海量书库
立即打开




引进式(2.77)中的λ值并求解E,发现式(2.84)给出能量表示式
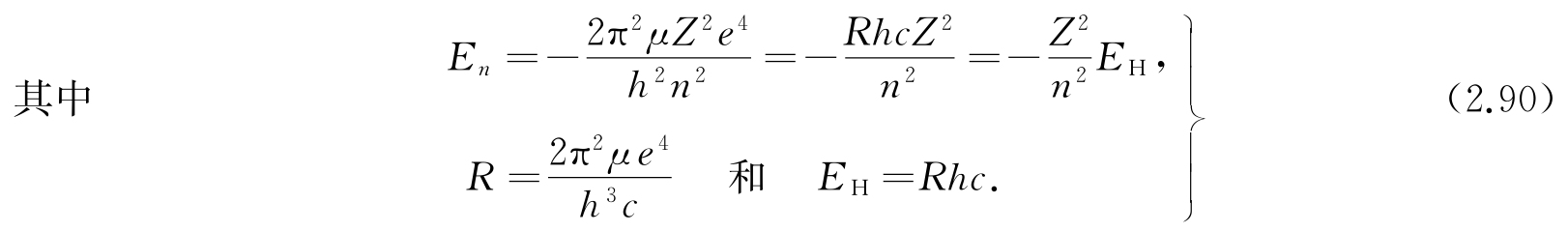
这里可以看出,类氢原子处在量子数n、l和m代表的状态时,能量和l、m无关,仅依赖于主量子数n. 既然m可以是零,方程(2.75)和(2.84)就指出n可以是数值1,2,3,…. 除了n=1以外,每个能级都是退化的,对应于同一能级可以有几个波函数的独立解. 与每一组不同的n、l、m值对应的波函数是独立的. 这些量子数的容许值是
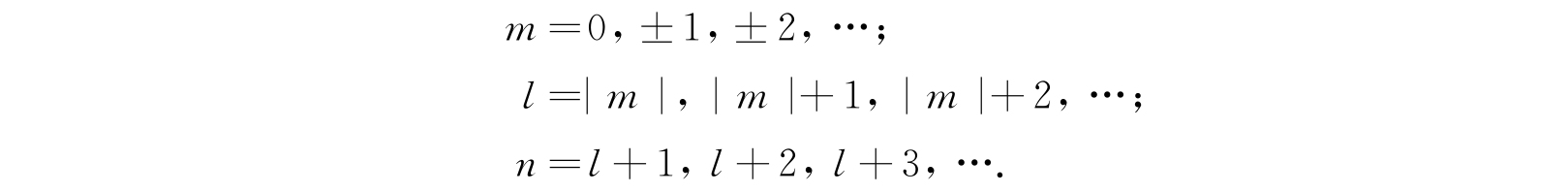
我们可以把它们改写成:
主量子数
n=1,2,3,…;
角量子数
l=0,1,2,…,n-1;
磁量子数
m=-l,-l+1,…,-1,0,+1,…,+(l-1),+l.
因此,对给定的n和l有2l+1个独立的波函数;对给定的n值有n 2 个独立波函数,也就是对每一能值有n 2 个独立波函数. 具有相同n和l的2l+1个波函数形成完整子群,具有同一n值的n 2 个波函数形成完整群.
对具有正E值的波动方程作类似处理,结论是对所有的正E值都有合适的解,因此它的能谱是连续的,而对负E值能谱是不连续的. 这一点可以从2.2节的一般讨论中预期到. 我们不在这里处理关于正E值的波函数,因为在以后的讨论中并不应用它们.