2.8　氢原子的内部动力学

现在我们转向氢原子的内部动力学问题. 首先我们看到方程（2.59）的解是

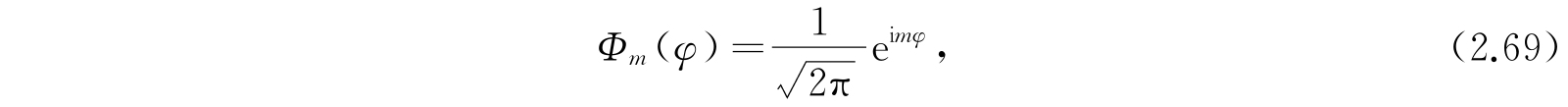
为了满足单值条件，参数m必须是整数. 因此m=0，±1，±2，±3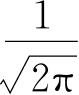，…. 是归一化因子，也就是

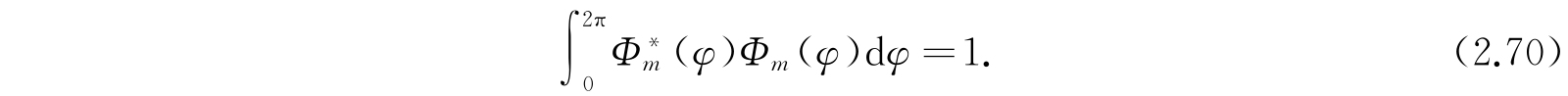
为了找函数Θ（θ），我们引进

z=cosθ，　（2.71）

方程（2.60）就变成

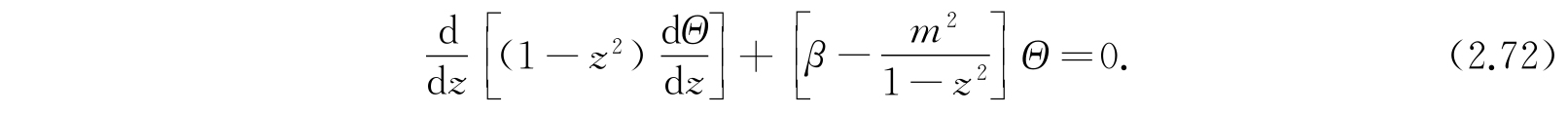
这个微分方程的解是熟知的关联勒让德（Legendre）函数 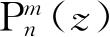，而这个函数的定义是

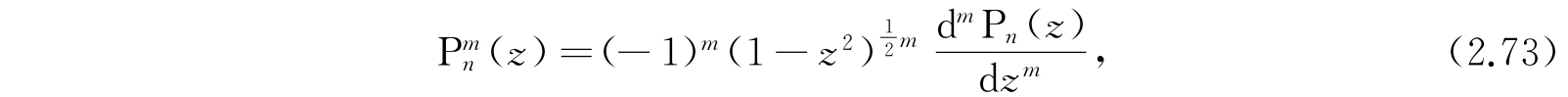
其中P _n （z）是勒让德n次多项式. 那么事情立刻很清楚：m必须是正的才不会使解在z=±1（θ=0，2π）时变为无穷大. 所以实际上这解应写成

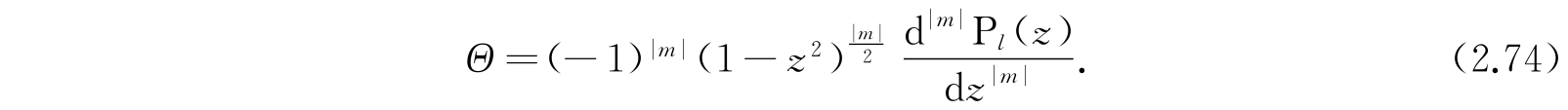
另外P _l （z）的次数l也必须是正整数，必须等于或大于|m|才不会使解等于零. 将这解代入方程（2.72）就得到

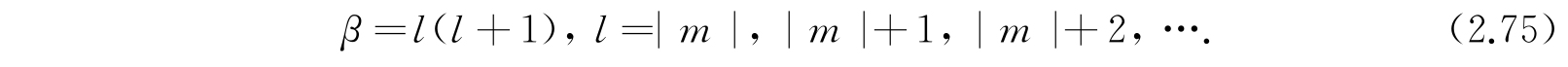
更详细的研究指出，这样规定的解是唯一可用的波函数Θ（θ）. 在物理术语中，m叫作磁量子数，而l是角量子数. 应该在这里着重指出，现在得到的Φ（φ）和Θ（θ）是与势能函数V（r）无关的，对任意的V（r）它们都适用，在以后我们将利用这个事实.V（r）的效应只对波函数R（r）出现，我们就来证明这一点.

利用式（2.75），R（r）的方程（2.61）就变成

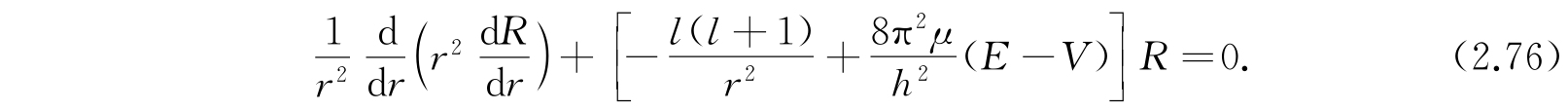
在库仑引力的作用下，V（r）=-Ze ² /r，Z是核电荷的数目，或者是原子序数. 让我们首先考虑E是负值的情形，这相当于总能量不足以使原子离解的情形. 引进符号

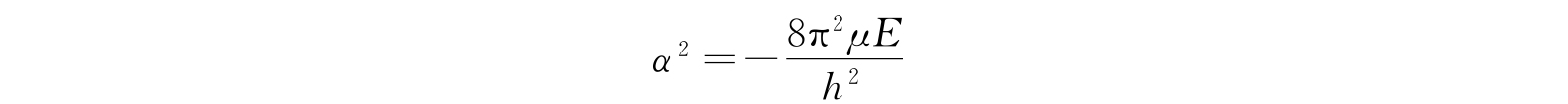
和

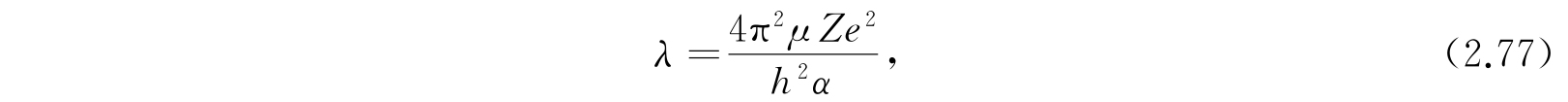
以及新的自变量

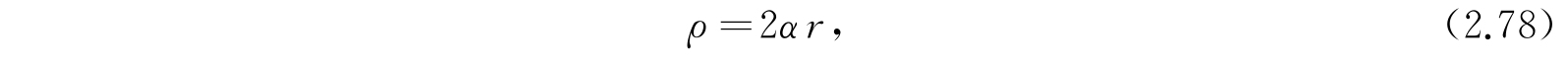
方程（2.76）变成

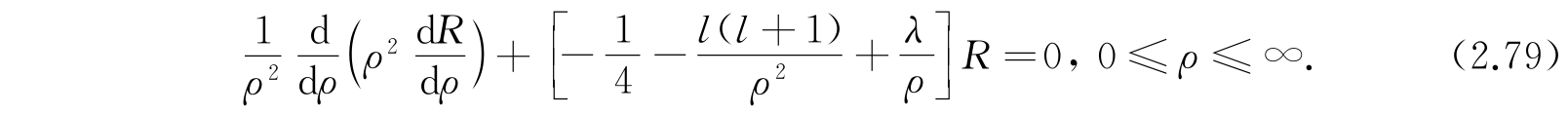
现在把因变量改变如下：

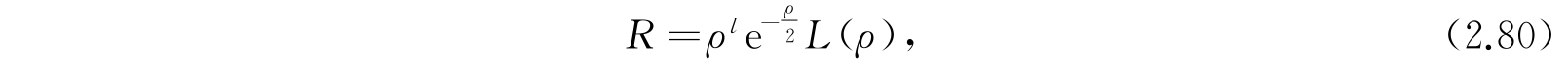
那么L（ρ）的方程是

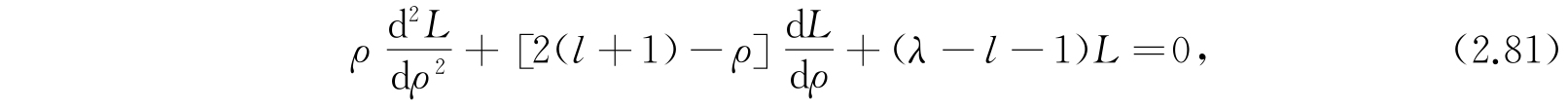
满足方程的解是关联拉盖尔（Laguerre）多项式 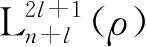，其中

λ=n，　n=整数　（2.82）

和

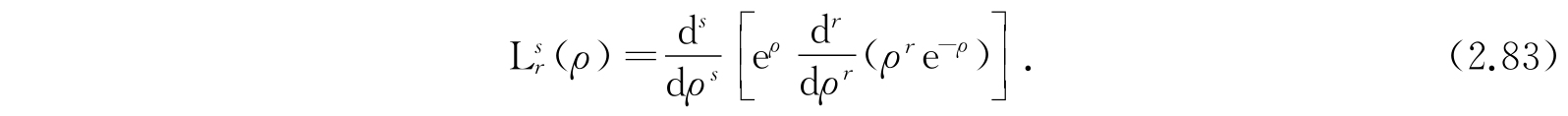
从方程（2.83）的定义，我们看到圆括弧中的量是一个r次的多项式. 为了使关联拉盖尔多项式不等于零，必须使

n=l+1，l+2，…，　（2.84）

n叫作主量子数.

利用勒让德多项式和拉盖尔多项式的已知性质，我们能够决定Θ（θ）和R（r）的归一化因子. 实际上，

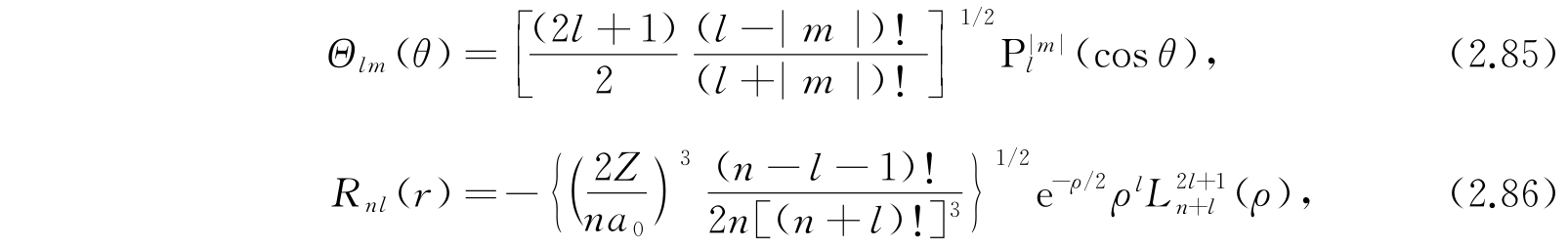
其中

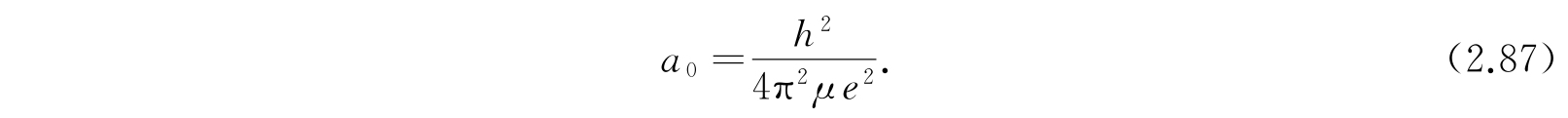
由于这些多项式是相互正交的，所以波函数ψ _nlm （r，θ，φ）=R _nl （r）Θ _lm Φ _m （φ）也是相互正交的，也就是

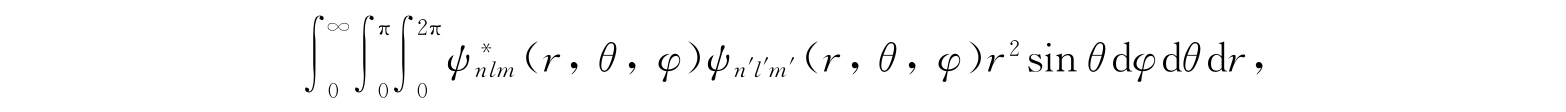
在n≠n′，l≠l′和m≠m′时等于零. 当n=n′，l=l′和m=m′时积分是1.

让我们作一个简单的数字计算：在最低能级，n=1，l=m=0，于是

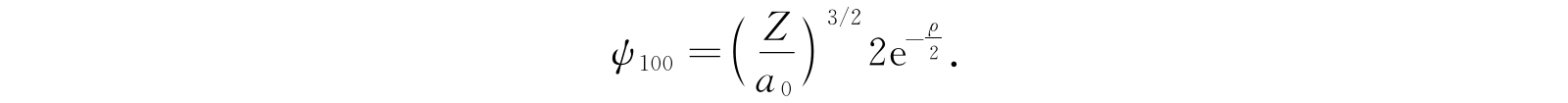
电子与核的平均径向距离

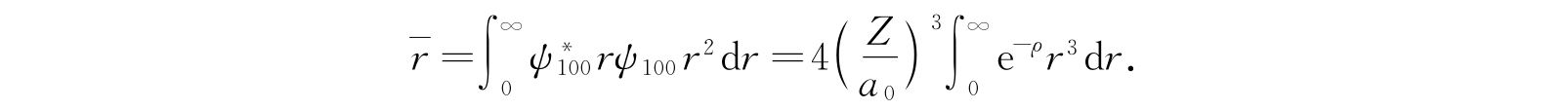
利用式（2.78），

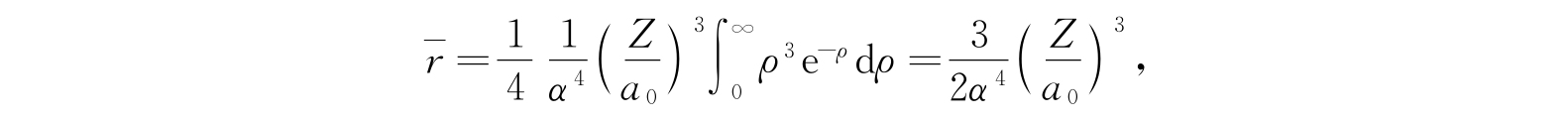
再利用式（2.77），我们最终得到

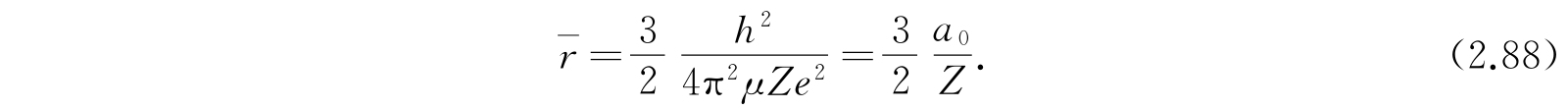
类似地，

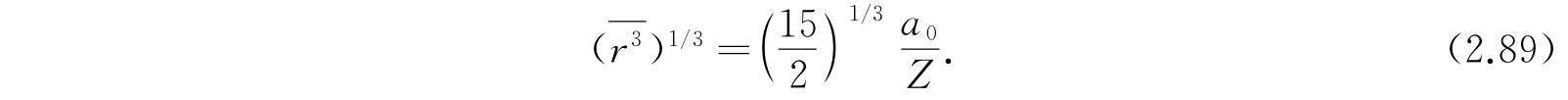
基于有效体积的观点，可以认为这是基态时原子的尺寸. 对氢原子，Z=1，a ₀ =0.529Å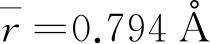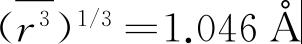； ， . 最后的数值与表1.7中列举的范德瓦耳斯半径1.3Å是接近的，这表明了我们的理论是与事实相符合的. Kgpg6NAdQRVghpi/iGc8HMc51G18qx6t5fti6MfUTLrKgRC3oF+Se5rPt18iyeat