下载掌阅APP，畅读海量书库
立即打开
在进行氢原子的内部动力学的详细计算以前，我们先研究由方程（2.54）描述的原子整体的运动. 我们用M表示体系的总质量m 1 +m 2 ，于是平动波函数就由下列方程决定：
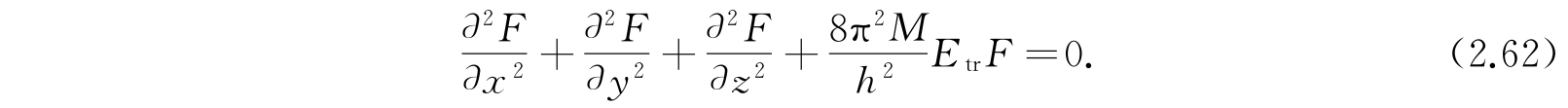
现在让我们试用解
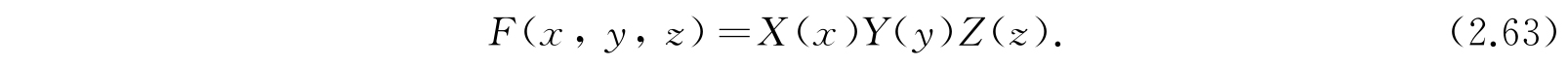
于是方程（2.62）给出
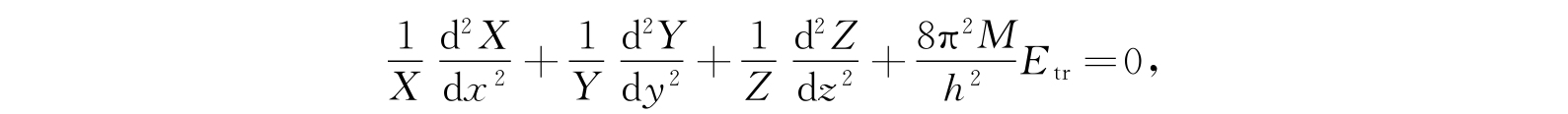
其中每一项应该是常数. 因而，我们可以令
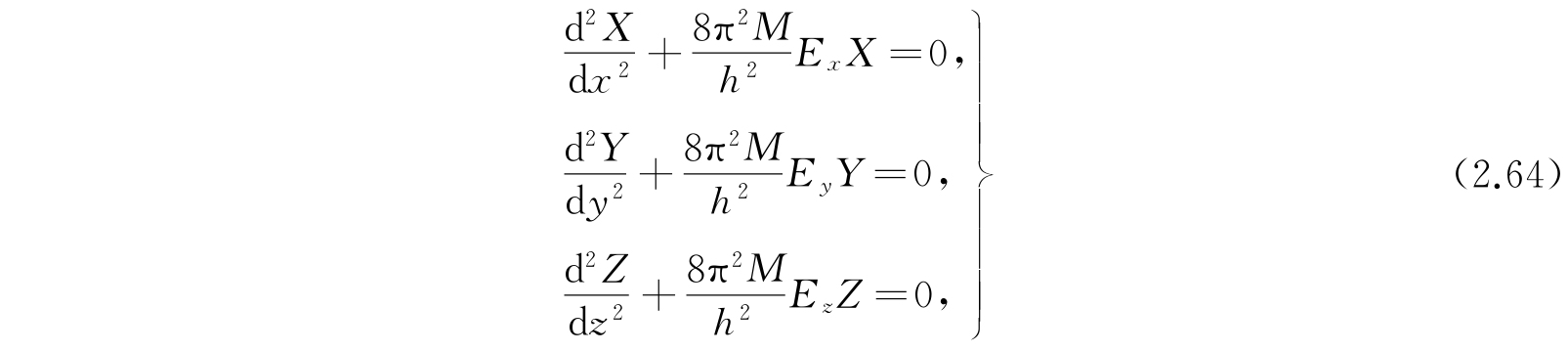
其中
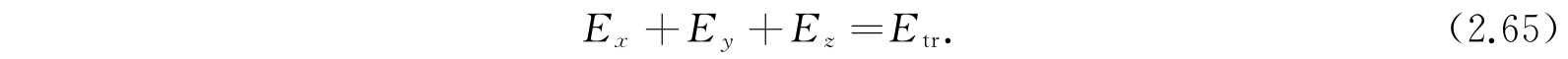
方程（2.64）的解是
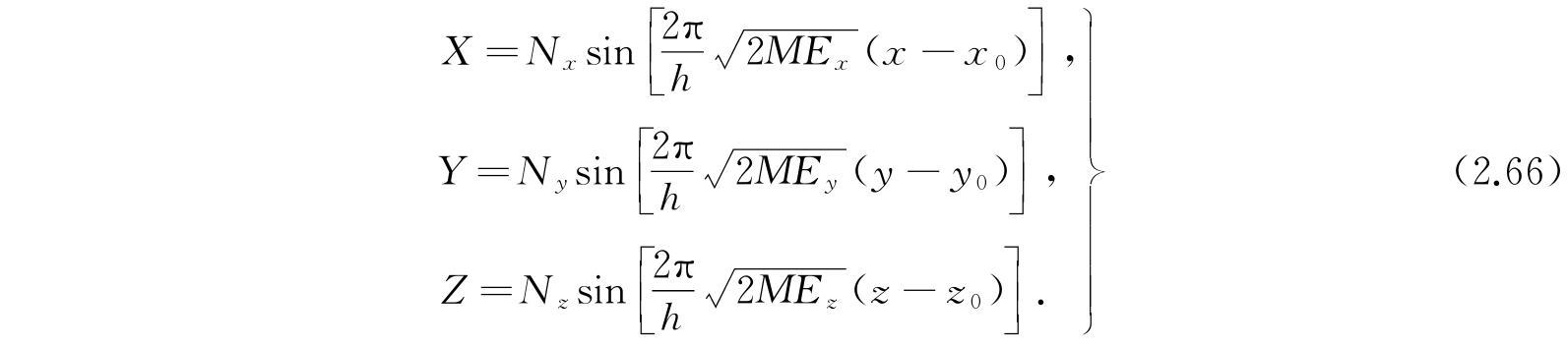
现在必须考察函数F，E tr =E x +E y +E z 应该取怎样的数值才能满足2.5节所规定的波函数条件. 因为正弦函数是连续的、单值的，并对辐角的所有实数值是有限的，加在E上的唯一限制是：E x 、E y 和E z 必须是正的，因此E tr 也只能是正的数值. 这样我们就得出结论：自由粒子可能的能值是连续的.
在讨论这一个体系的波函数的物理意义时，让我们首先考虑E y 和E z 为零，而E x =E tr 的波函数所代表的物理状态. 函数
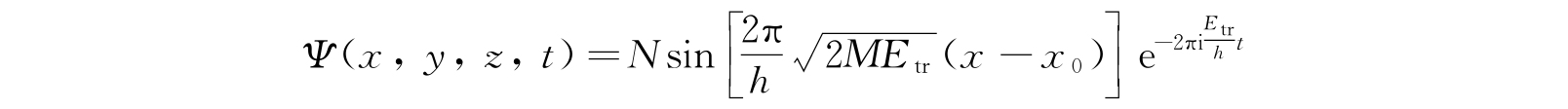
是一组波前与x轴垂直的驻波. 波长由下式给定：
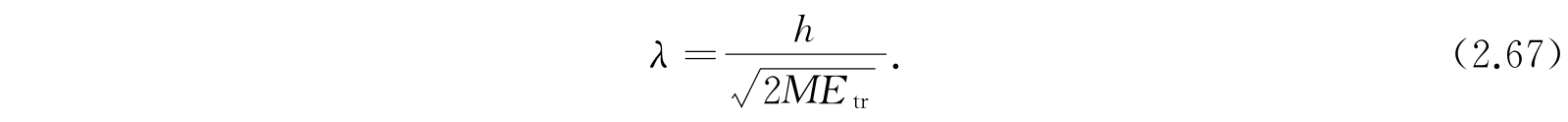
在经典力学中以速度v运动的质量为M的自由粒子具有总能量
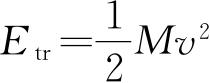. 或者我们把动能写为
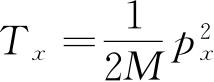，T
x
的平均值可以计算如下：
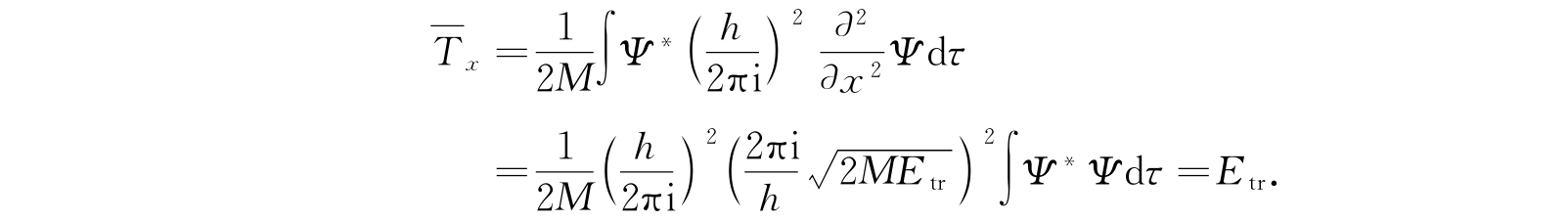
类似地，我们能找到
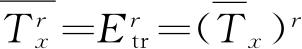，按照2.3节的讨论，这表示沿x轴运动的动能有确定的数值E
tr
，它的概率分布函数除对这数值外都为零，因而我们有
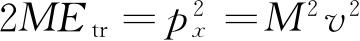. 方程（2.67）就可以写成
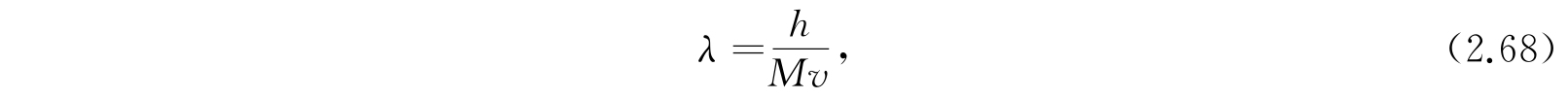
这是和具有质量M及速度v的运动粒子相关联的德布罗意（de Broglie）波长的表示式.
利用单色平面波函数
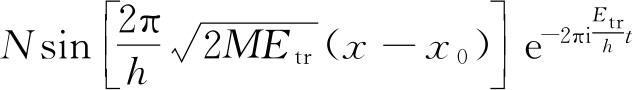，我们可以发现p
x
的平均值
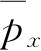为零. 这不能解释成粒子沿x轴的运动方向是时正时负，而是粒子沿其中一个方向运动，但在两个运动方向上的概率相等. 为了作出一个代表运动粒子的波函数Ψ，可以用基本解叠加，这里不再进行描述，读者可以参阅量子力学的书籍.