下载掌阅APP，畅读海量书库
立即打开
现在我们来说明氢原子的量子力学计算. 我们将会看到，由于氢原子是两质点（一个电子和一个质子）组合，从这一概念出发，我们能够很精确地计算得到氢原子的定态和其他重要性质. 质子和电子之间可能有的相互作用是万有引力和静电力. 但是静电力，或者是库仑力远比万有引力要大得多，所以我们可以忽略掉万有引力. 为了广泛起见，我们令核电荷是+Ze（对质子Z=1），电子电荷是-e. 那么体系的势能就是-Ze 2 /r，这里r是核和电子间的距离. 假使我们将核和电子的笛卡儿坐标写作x 1 、y 1 、z 1 和x 2 、y 2 、z 2 ，而将它们的质量写作m 1 和m 2 ，则波动方程的形式就成为
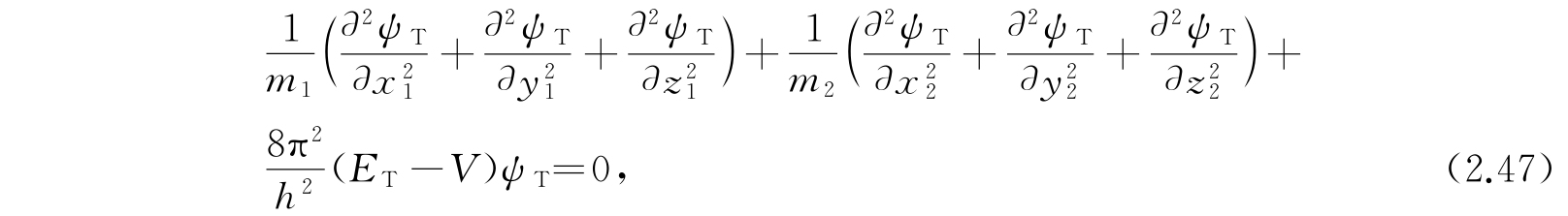
其中
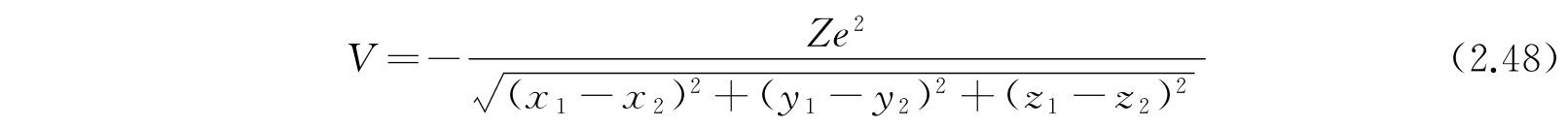
这里E与ψ的下标T是表明整个体系的物理量，它们包含有六个坐标.
波动方程立刻可以分离成两个，一个代表把原子作为整体的平移运动，另一个代表两个粒子的相对运动. 当势能V像上面所说那样，只是两个粒子的相对坐标的函数，也就是V=V（x 1 -x 2 ，y 1 -y 2 ，z 1 -z 2 ），那么并不需要知道势能函数的具体形式，就可以完成波动方程的分解. 例如，氢原子处在z方向的恒定电场中时，由于场强E产生的势能是eEz 2 -eEz 1 =-eE（z 1 -z 2 ），就可以包括在这类情形中.
为了有效地进行分离，我们引进新变量x、y、z，它们是体系质量中心的笛卡儿坐标；此外r、θ、φ是第二个粒子相对于第一个粒子的极坐标. 这些坐标和两个粒子的笛卡儿坐标的关系如下：
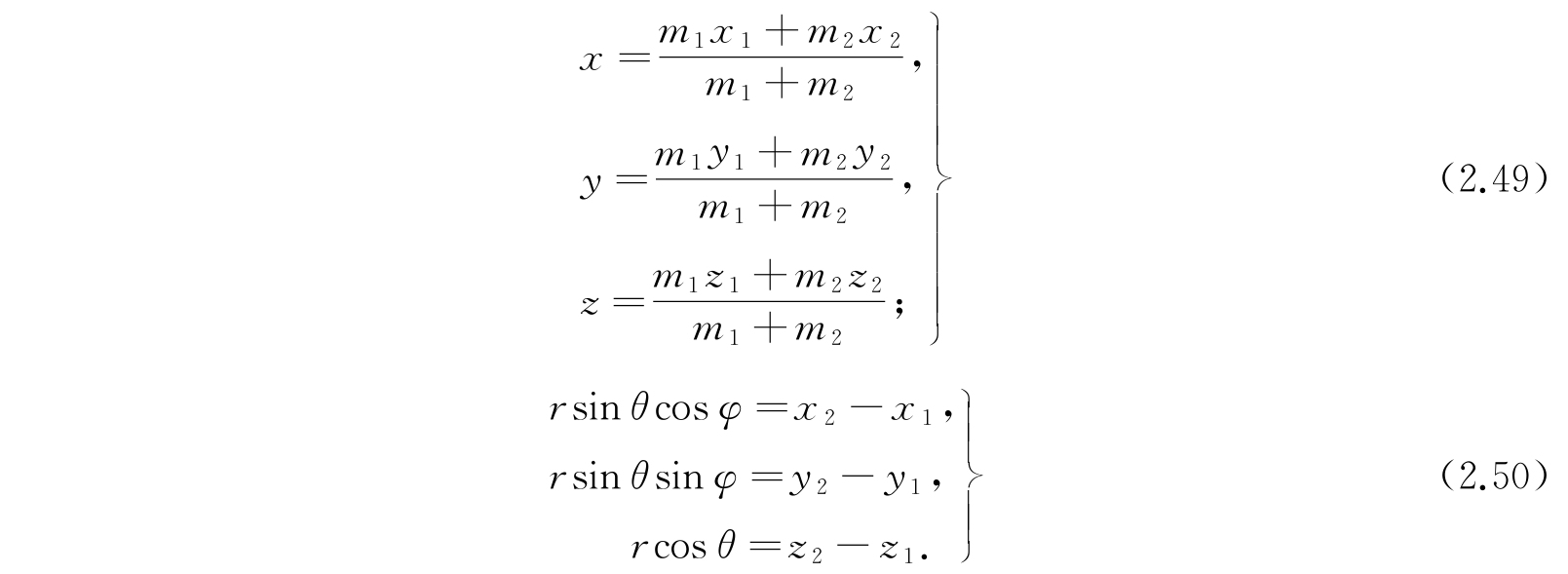
新变量的引入是很容易完成的，这样，方程（2.47）就转化成下列形式：
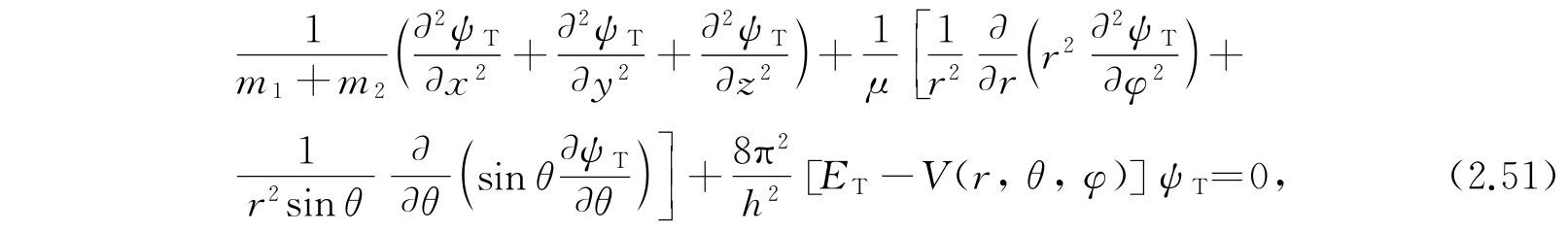
其中引进的符号μ代表下列数量：
μ是体系的约化质量. 如果m 1 和m 2 有很大的差别时，μ接近于较小质点的质量. 我们注意到第一个括弧中是ψ T 在笛卡儿坐标（x，y，z）中的拉普拉斯算符，而第二个大括弧中是ψ T 在极坐标（r，θ，φ）中的拉普拉斯算符. 所以我们企图来分离这个方程，而把ψ T 表示为x、y、z的函数和r、θ、φ的函数的乘积：
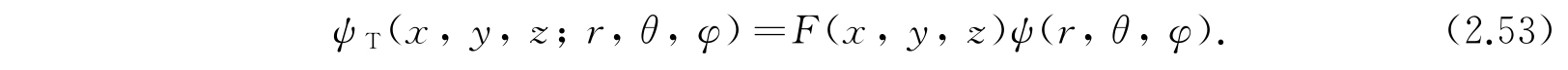
把方程（2.53）代入方程（2.51），就得到
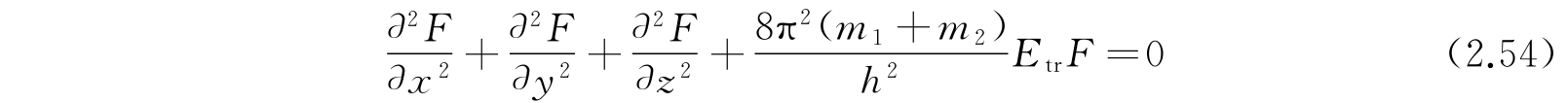
和
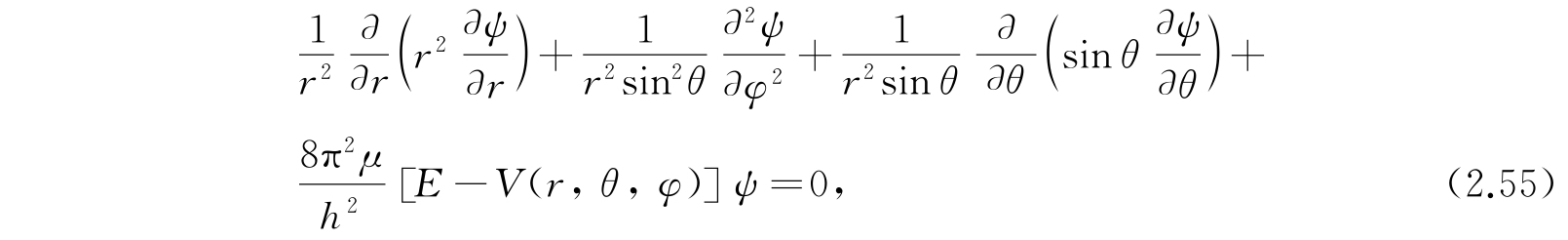
并且
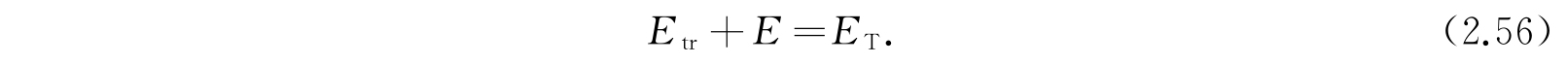
这一方程系有一个简单的解释：方程（2.54）显然是一个质量等于m 1 +m 2 （体系的质量总和）的粒子的波动方程，其空间坐标为m 1 和m 2 的质量中心. 这里的势能是零，所以它实际上描述的是自由粒子的运动；E tr 也就是自由粒子的平动能. 方程（2.55）是具有势能V和约化质量μ的粒子的波动方程，它描述了体系的内部运动，E是体系的内部能量.
如果我们再限制势能V只是r的函数，
V=V（r），
方程（2.55）能够进一步分离. 将ψ写成
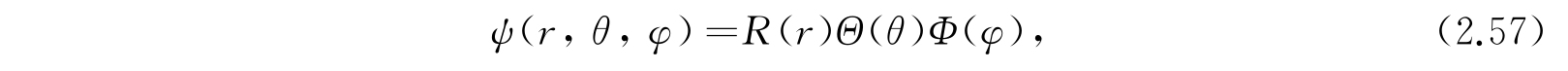
代入方程（2.55）并除以RΘΦ，就变成
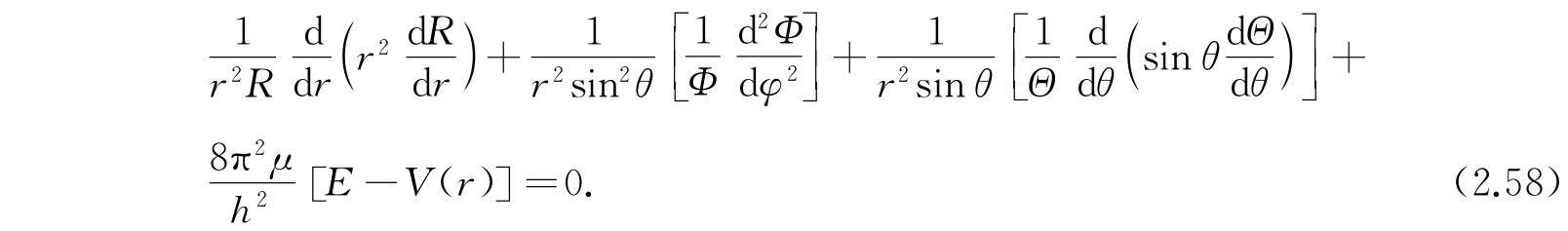
在乘上r
2
sin
2
θ以后，第二项留下的部分
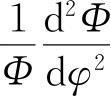只能够是独立变量φ的函数，但从整个方程来看，却等于一些与φ无关的项. 所以这一项应该等于常数，我们把这个常数写作-m
2
：
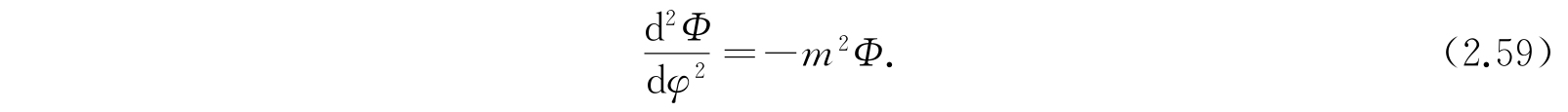
于是包含有θ与r的方程可以写成
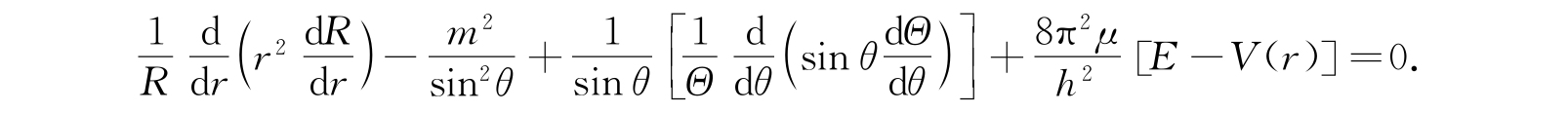
这方程的第二项和第三项与r无关，而余下的部分和θ无关，所以我们能够使这两个部分的每一部分都等于常数. 令包含θ项的部分等于常数-β，而包含r项的部分等于+β，我们得到两个方程
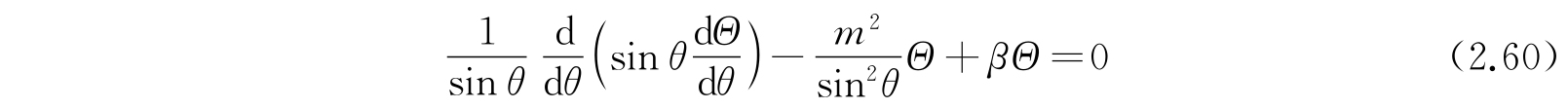
和
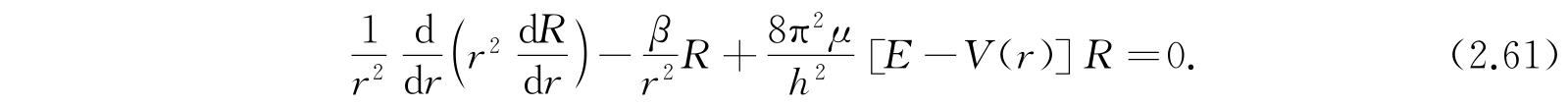
为了确定容许的能值，现在可以解方程（2.59）、（2.60）和（2.61）. 解的步骤如下：首先找出方程（2.59）的合适解和参数m的相应数值. 将这些m值代入方程（2.60），就能发现只有β在某些值时方程（2.60）才有合适的解. 最后把这些结果引进方程（2.61），我们就找到能级E.