下载掌阅APP，畅读海量书库
立即打开
对三维空间中相互作用的N个粒子的体系，薛定谔方程和前节中处理的一自由度简单体系十分相似. 含时方程是一个有3N+1个独立变量（N个粒子的3N个笛卡儿坐标和时间）的偏微分方程，波函数是这3N+1个变量的函数. 和简单体系一样，利用类似的变换可以使含时方程分离成只含时间的方程和包含3N个坐标的振幅方程. 只含时间的方程和简单体系的方程相同，所以对点粒子的一般体系，定态波函数与时间的关系与一维情形相同. 但是振幅方程就不是原来的一个变量的常微分方程，而是3N个独立变量即3N个坐标的偏微分方程. 为了方便起见，我们说这是3N维位形空间中的方程，意思就是要找一个对3N个笛卡儿坐标x 1 ，…，z N 的一切数值（-∞到+∞）都能满足方程的解；这样的解是3N个坐标的振幅函数，也就是位形空间中的一个函数. 位形空间中的一个点与坐标x 1 ，…，z N 的一组确定数值对应，因此在一般空间中确定了粒子的位置，也就是确定了体系的位形. 关于一般体系的波动方程，波函数的附加条件，以及波函数的物理意义是和一自由度体系相似的，唯一的变化是因位形空间的维数增加而引起的.
让我们考虑包含N个点粒子的体系：这N个粒子的质量为m 1 ，m 2 ，…，m N ，处在以势能函数V（x 1 ，y 1 ，…，z N ；t）表示的力场影响下，在三维空间中运动. 这里x 1 ，…，z N 是N个粒子的3N个笛卡儿坐标. 代表粒子间的相互作用或者粒子和外力场的相互作用，或者是两种情况共存的势能函数V只可以是3N个坐标的函数，也可以是时间的函数. 在前一种情形，V=V（x 1 ，…，z N ），我们的体系也就是保守体系. 我们的主要兴趣就集中在这一类型的体系上，因此，我们的讨论就只限于这类体系. 这类体系的薛定谔波动方程是
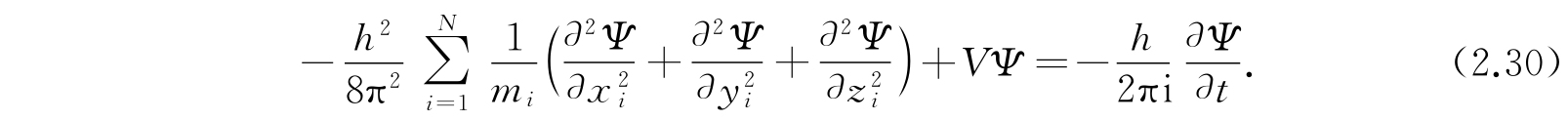
这个方程经常写成
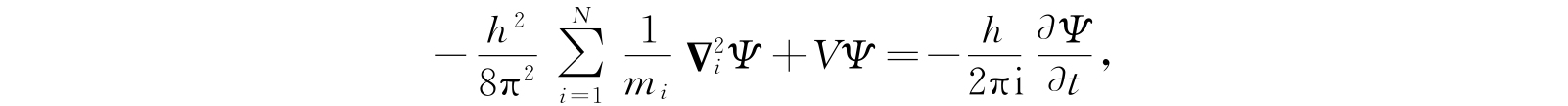
其中
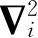是第i个粒子的拉普拉斯算符，也就是
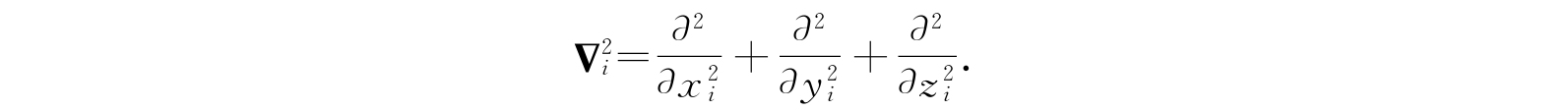
可以注意到，一般体系的含时薛定谔方程和经典能量方程在形式上是相互关联的，其关系和前节中的一自由度体系相同. 对点粒子的牛顿体系有能量方程
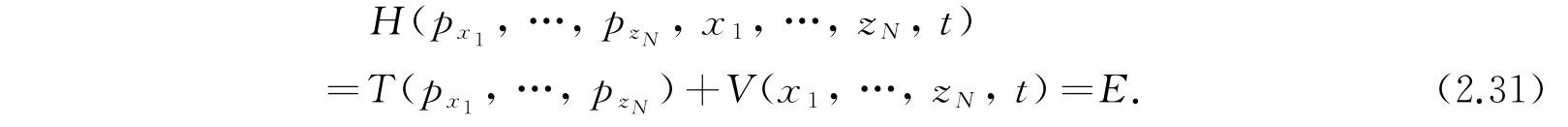
把动能用动量表出来就变成
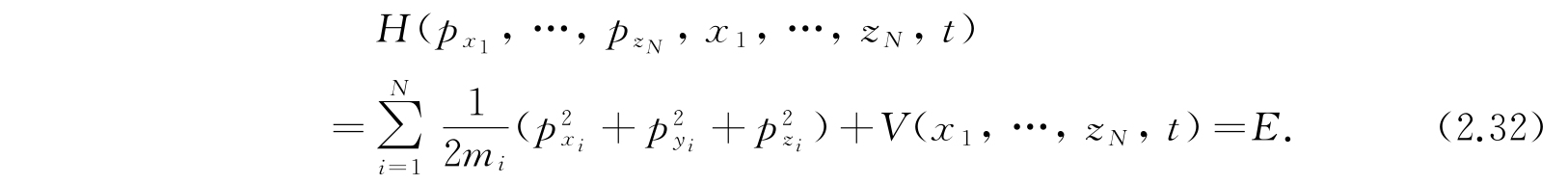
现在用算符
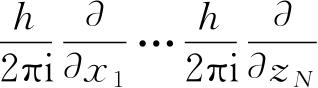代替
，…，
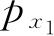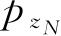，又以算符
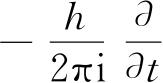代替E，并引进Ψ（x
1
，…，z
N
，t），使算符作用在它上面，方程就变为
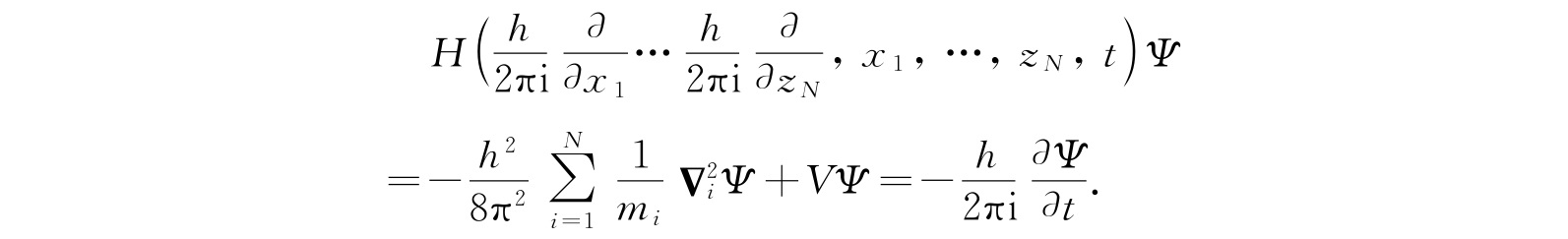
这与方程（2.30）一致. 恰如在一维情形中那样，波动方程可以形式地简写成
HΨ=EΨ. （2.33）
现在让我们把注意力转到保守体系上，这时V只是3N个坐标的函数. 解这一情形中的波动方程，我们可以像求解2.1节中的简单问题一样地进行. 这就是令
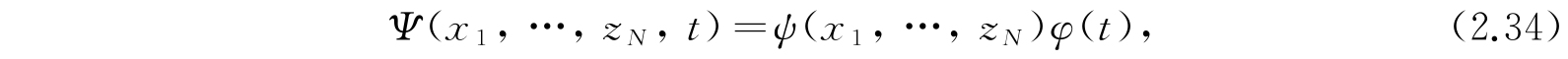
代入方程（2.30）中，我们就有对ψ和φ的两个方程：
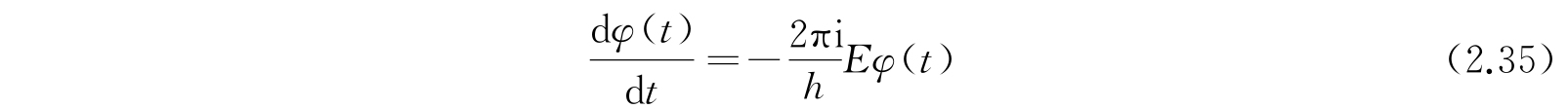
和
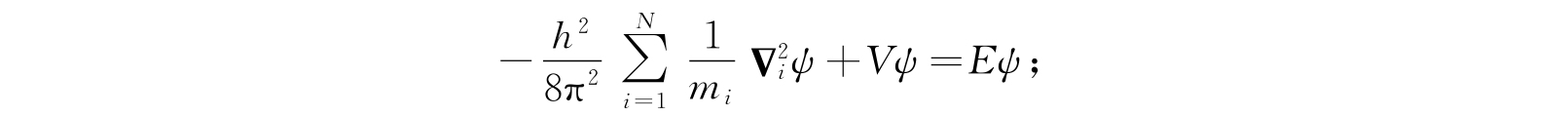
后一方程常写为
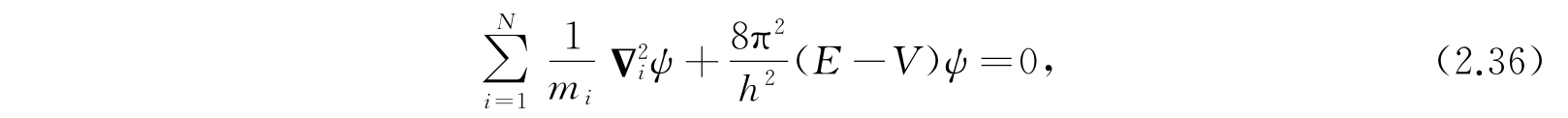
这是点粒子保守系的薛定谔振幅方程. 为了能够把解采纳作波函数，方程的解要满足2.2节所给的辅助条件. 这些条件必须在全部位形空间中成立，也就是对3N个坐标中的每一个从-∞到+∞间的所有数值都成立. 就像一维情形一样，只对能量参数E的某些数值有适合的解存在. 这些数值可以是间断的，或连续的，或两者都有.
通常可以用3N个整数来标记能量参数的各个有效值和对应的振幅函数，它们代表与3N个坐标结合的量子数n
1
，…，n
3N
. 结合的方式将用以后的例子来说明. 现在我们用一个字母n代表所有的量子数n
1
，…，n
3N
，并且用简单的符号E
n
和ψ
n
代替
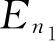，…，n
3N
和
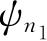，…，n
3N
.
对φ（t）的方程（2.35）积分，得
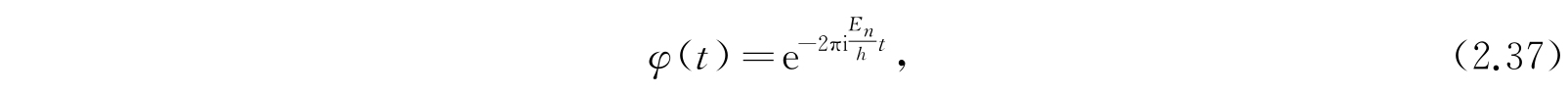
这和一维情况完全相同. 波动方程的各个特殊解将是
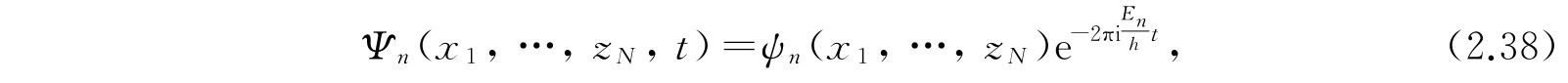
这代表了体系的各个定态. 波动方程的一般解是
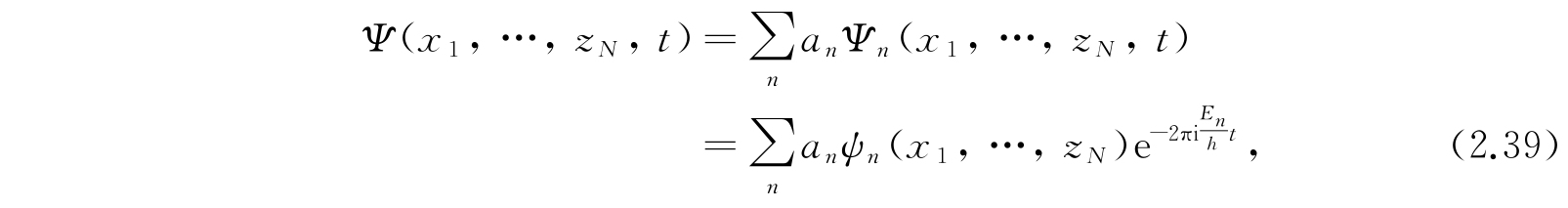
其中a
n
是常数. 符号
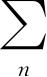代表对所有的间断E
n
值求和以及对所有的连续E
n
值积分.
波函数Ψ * （x 1 ，…，z N ，t）是共轭波动方程
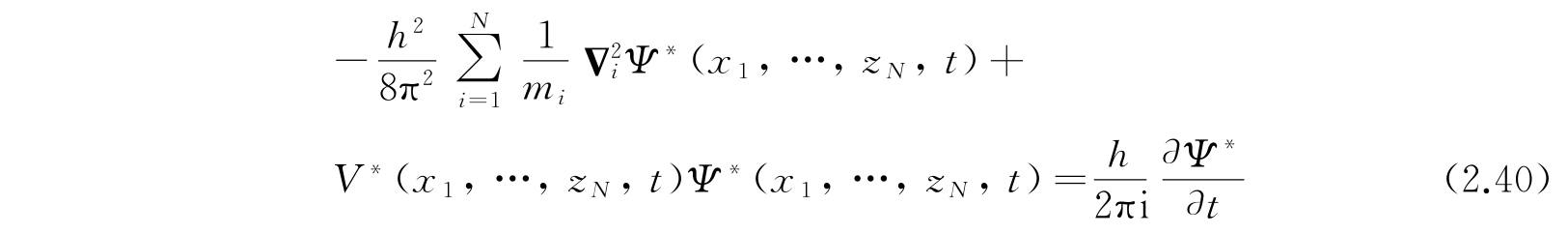
的一个解. 对保守体系，这个方程的一般解是
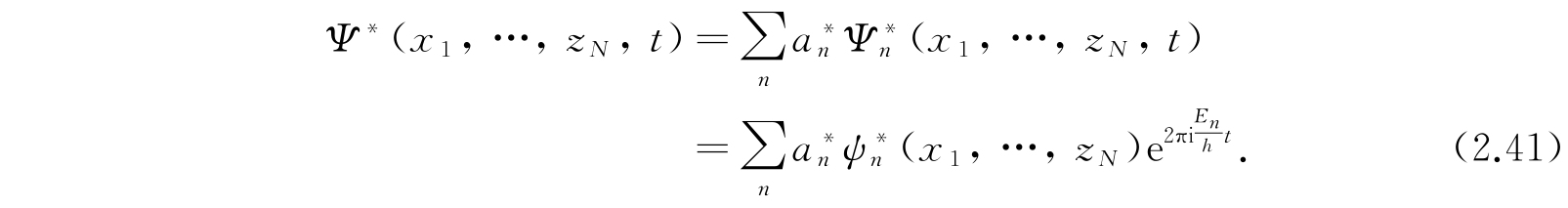
对该一般体系波函数的物理意义与2.3节中关于一自由度体系的讨论非常相似. 因此， 量 Ψ * （x 1 ，…，z N ，t）Ψ（x 1 ，…，z N ，t）dx 1 ，…，dz N 是物理状态由波函数 Ψ（x 1 ，…，z N ，t） 所代表的体系在时间 t 处在位形空间的体积单元 dx 1 ，…，dz N 中的概率 .Ψ * Ψ就起着体系位形的概率分布函数的作用. 函数Ψ（x 1 ，…，z N ，t）必须归一化，就是要满足方程
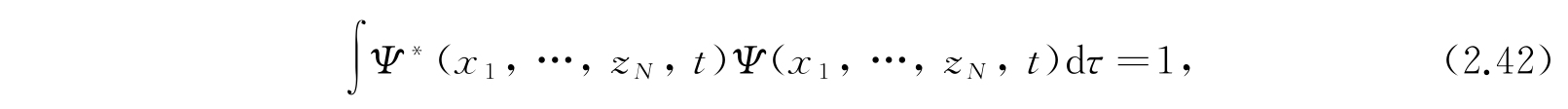
其中符号dτ代表位形空间中的体积单元dx 1 ，…，dz N ，而积分拓展到全部位形空间. 按照方程
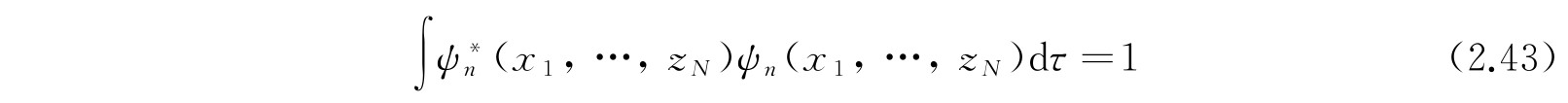
也可以使振幅函数ψ（x 1 ，…，z N ）归一化.
更进一步，还可以用
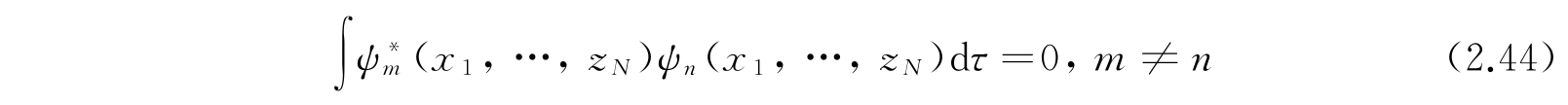
使波函数正交. 如果用这样一些正交归一的波函数，将一般的波函数Ψ如方程（2.39）和（2.41）展开，其归一化条件为
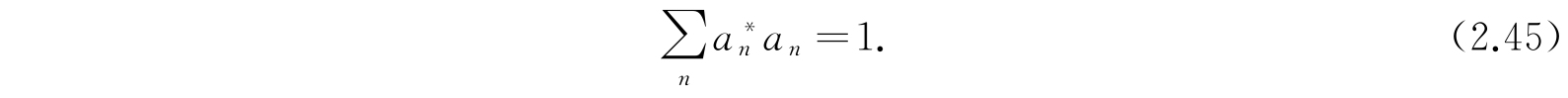
和2.3节类似的论证说明Ψ
n
（x
1
，…，z
N
，t）=ψ
n
（x
1
，…，z
N
）
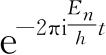给出的概率分布函数是和时间无关的，因此与定态对应.
根据2.3节所示的线索，可以给波函数指出更一般的物理解释. 如果G（
，…，
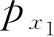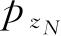，x
1
，…，z
N
，t）是体系的某一个动力学的量，它的平均值用
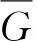表示，于是
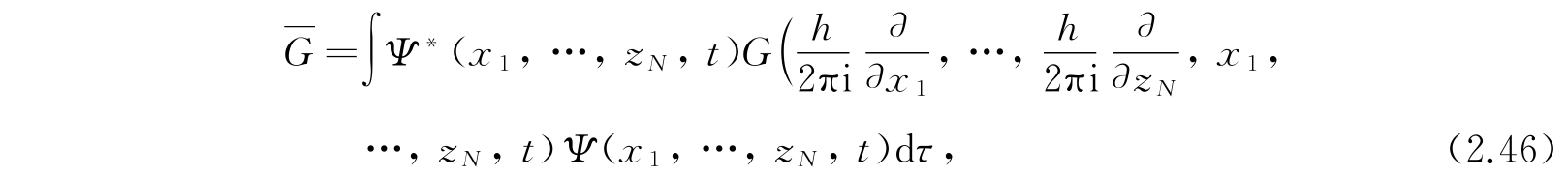
其中算符G是通过G（
，…，
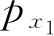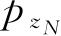，x
1
，…，z
N
，t）把其中的
，…，
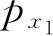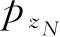代之以
，…，
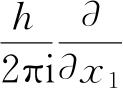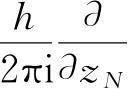而得来的. 积分也拓展到全部的位形空间.