




我们考虑波动方程的某一个给定的一般解Ψ(x,t). 在给定的时刻t,Ψ和它的共轭复数的乘积Ψ * (x,t)Ψ(x,t)是一个对-∞到+∞中间的所有x的值(也就是一维体系的全部位形空间)都有定义的函数. 关于Ψ的物理意义,我们作如下的假设:
量Ψ * (x,t)Ψ(x,t)dx是物理状态由波函数Ψ(x,t)所代表的体系在时间t处在位形空间的x到x+dx区间内的概率. 位形由位形空间中的一个点表示. 换句话说,Ψ * (x,t)Ψ(x,t)是体系位形的概率分布函数. 在上面讨论的简单例子中,Ψ * (x,t)Ψ(x,t)dx是粒子在时刻t处在x到x+dx间的概率.
为了使这一假设合理,函数Ψ(x,t)必须归一化;因为在全部位形空间中找到粒子的概率必然等于1,这就要求适当选择方程(2.11)中的常数a n ,使得
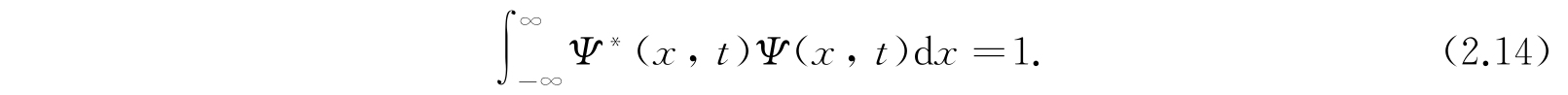
我们可以把各个振幅函数ψ n (x)也独立地归一化,使它们满足方程
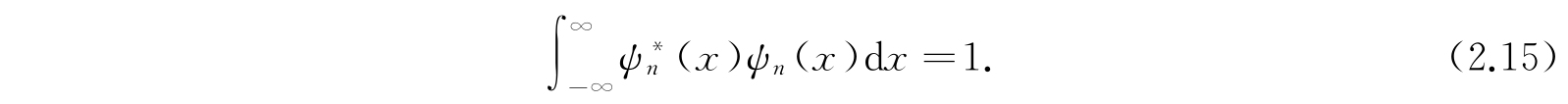
同时可以证明,振幅方程的独立解总是可以满足积分关系式
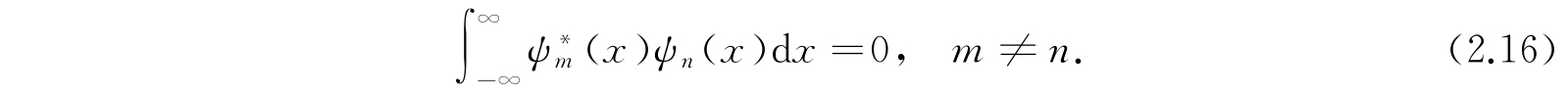
这时,我们说函数是互相正交的. 这样一组满足式(2.15)和(2.16)的ψ叫作一组正交归一函数. 利用这些关系式就可以发现,当系数a n 满足关系式
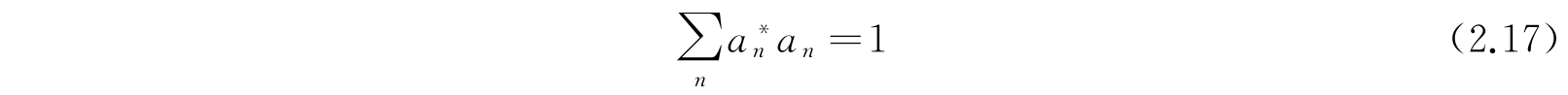
时,
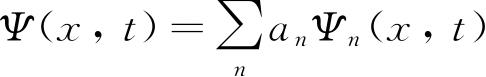 就归一化了.
就归一化了.
让我们考虑某一个体系的概率分布函数Ψ
*
,这个体系处在波函数Ψ(x,t)=
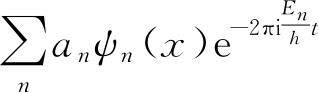 和它的共轭复数
和它的共轭复数
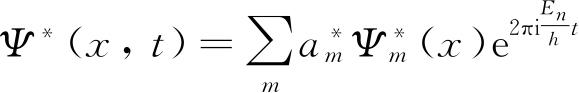 所代表的状态中. 将这两个级数乘在一起,Ψ
*
Ψ就有下面的形式:
所代表的状态中. 将这两个级数乘在一起,Ψ
*
Ψ就有下面的形式:
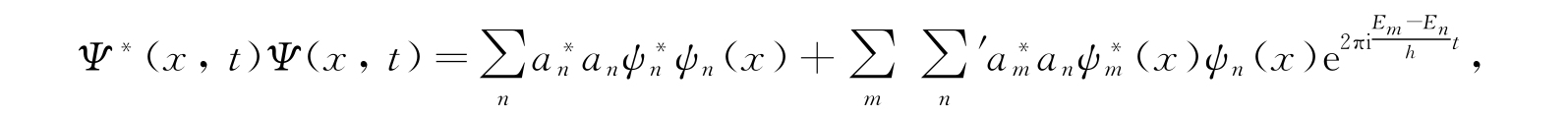
其中∑′表示只包括m≠n的项. 一般来说,既然二重求和号中包含有时间的指数因子,那么概率分布函数就和时间有关;而体系的性质也就依赖于时间而变化. 只有在对应于某一本征值E
n
的系数a
n
以外其他系数a
n
都等于零的时候,Ψ
*
Ψ才和t无关. 在这一情形中,波函数将只有一项,
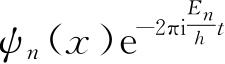 ;振幅函数ψ
n
(x)是振幅方程的特殊解. 对这样一种状态,由概率分布函数给出的体系性质也和时间无关,因此这种状态称为定态.
;振幅函数ψ
n
(x)是振幅方程的特殊解. 对这样一种状态,由概率分布函数给出的体系性质也和时间无关,因此这种状态称为定态.
假使我们问:“在时间t,物理位形由波函数Ψ代表的体系量,它的坐标x将会得到怎样的平均值?”那么上述对Ψ * Ψ给的解释就给出解答:
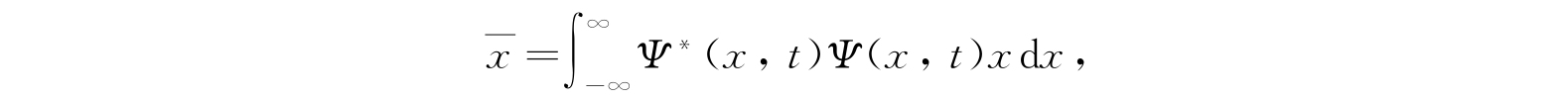
也就是,x的值对所有位形进行了平均,而用函数Ψ * Ψ作为权重或概率函数. 类似的积分对坐标x的任意函数F(x)给出平均值:
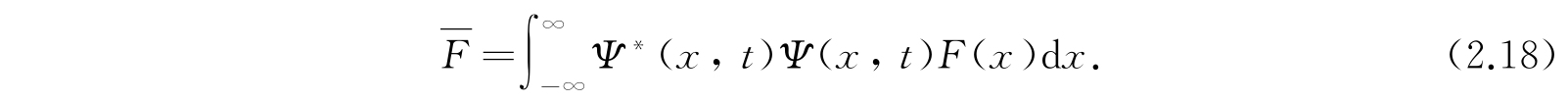
为了能够求得包含动量p x 和坐标x的更一般的力学量G(p x ,x)的平均值,我们作更一般的假设如下:
对某一个物理位形由波函数Ψ(x,t)代表的体系,其力学量G(p x ,x)的平均值将由下列积分给出:
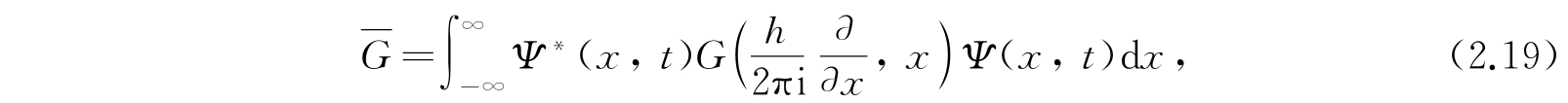
其中算符G是作用在Ψ(x,t)上的,而在G(p
x
,x)中用
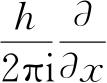 代替p
x
,这里的积分伸展到体系的全部位形空间.
代替p
x
,这里的积分伸展到体系的全部位形空间.
一般来说,G的测量结果并不由这一
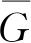 的表示式给定.
的表示式给定.
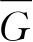 实际上是对相同体系(位形由Ψ代表)同时测量的平均值,或者是对同一体系重复测量的平均值,每次测量前必须使体系恢复同一位形. 例如,如果Ψ对x值的某一个区间是有限的(图2.2),那么x的测量值就可以是这一区间中的任何数值,出现的概率为Ψ
*
Ψ. 只有当除x=a外,Ψ
*
Ψ对所有的x值都为零,就像图2.2中的曲线B所示的那样,在测量x时所得到的特殊值x=a的概率才能等于1. 在这种情形里,测量x′得到a
r
的概率是1;所以对这样一个概率分布函数有
实际上是对相同体系(位形由Ψ代表)同时测量的平均值,或者是对同一体系重复测量的平均值,每次测量前必须使体系恢复同一位形. 例如,如果Ψ对x值的某一个区间是有限的(图2.2),那么x的测量值就可以是这一区间中的任何数值,出现的概率为Ψ
*
Ψ. 只有当除x=a外,Ψ
*
Ψ对所有的x值都为零,就像图2.2中的曲线B所示的那样,在测量x时所得到的特殊值x=a的概率才能等于1. 在这种情形里,测量x′得到a
r
的概率是1;所以对这样一个概率分布函数有
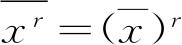 . 数学家也曾经指出:力学量G的概率分布属B型的充分条件是等式
. 数学家也曾经指出:力学量G的概率分布属B型的充分条件是等式
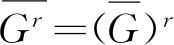 对所有r值成立,也就是G可以精确地测到.
对所有r值成立,也就是G可以精确地测到.
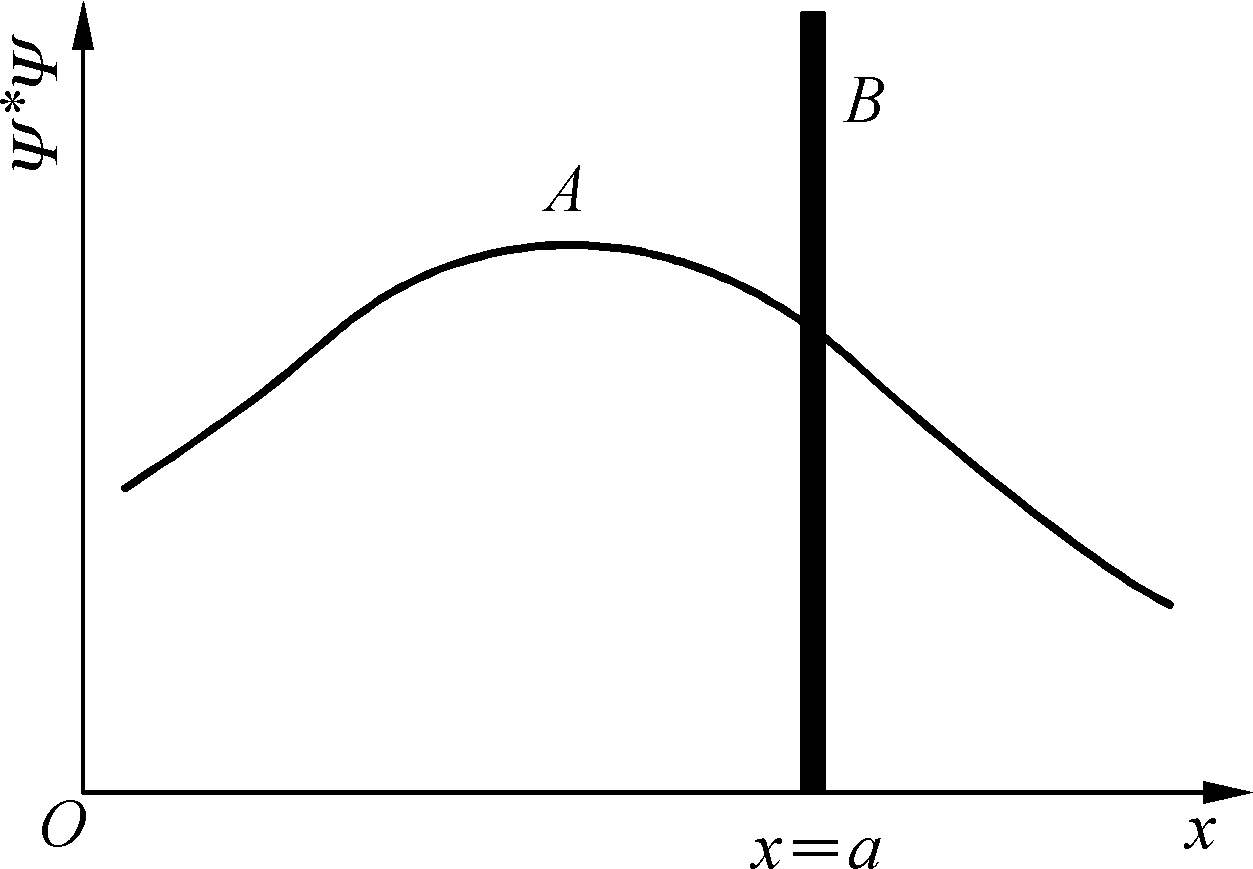
图2.2 体系处于Ψ时,x的测量值
甚至在体系处于波函数
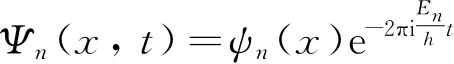 代表的定态时,对一个任意的力学量也只能测出一个平均值. 但是与哈密顿函数H(p
x
,x)对应的定态体系的能量,却有一个确定的数值等于解波动方程时得到的本征值E
n
,所以体系处在定态的时候,能量可以精确地测到. 为了证明这一点,我们计算
代表的定态时,对一个任意的力学量也只能测出一个平均值. 但是与哈密顿函数H(p
x
,x)对应的定态体系的能量,却有一个确定的数值等于解波动方程时得到的本征值E
n
,所以体系处在定态的时候,能量可以精确地测到. 为了证明这一点,我们计算
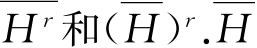 由积分
由积分
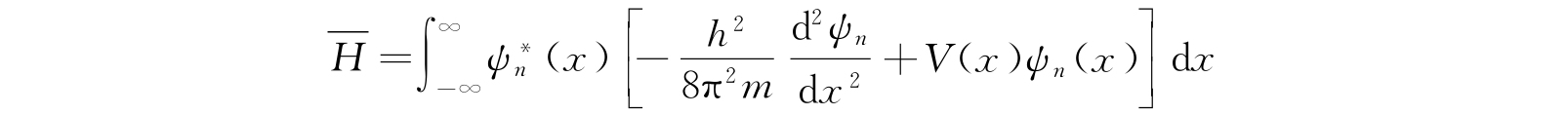
给出,式中原有的包含时间的因子等于1,所以不再出现了. 利用方程(2.9),
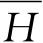 就化为
就化为
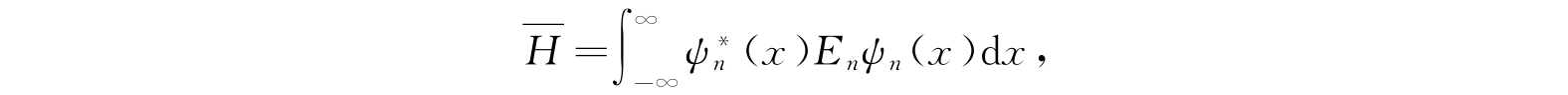
或者,因为E
n
是常数,且
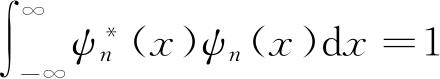 ,故
,故
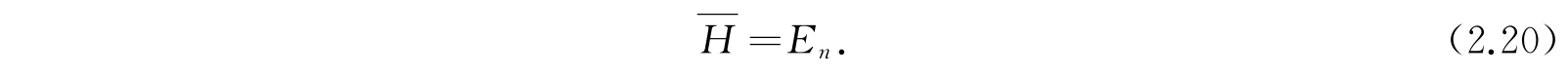
用类似的方法,重复应用方程(2.9),就能得到
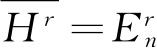 . 这样我们就证明了
. 这样我们就证明了
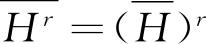 ,根据前面的论证,体系的能量就有确定的数值E
n
.
,根据前面的论证,体系的能量就有确定的数值E
n
.