（六）作图题

55．预备问题（a)引三等分直角的直线。（b)作二边为 8 分、10 分，夹角为60°的三角形。

几何学上也研究作成适合于已知条件的图形的方法。关于这一类的问题，名叫作图题。

解作图题得使用有分划的直尺，即尺度，分度器，圆规和三角板。到第二编第三章时，使用的器械，是只限于无分划的直尺及圆规，不得使用别种器械，而研究解作图题的方法；现在则可以用上记四种器械，并无限制。

练习问题

1．于一直在线的一定点，引其垂线（三角板）。

2．从一直线外的一定点，引其垂线（三角板）。

3．二等分一已知的线段（尺度）。

4．引直角的二等分线（直尺和分度器）。

5．引一已知角的二等分线（分度器和直尺）。

6．过一直在线的一定点，引与此直线成 60°角的直线（分度器和直尺）。

7．过一直线 AB 上的一定点 C 引与此线成已知角α的直线（分度器和直尺）。

8．已知二点 A ， B 和二线段 a ， b ；求一点，使从 A 到此点的距离等于 a ，从 B 到此点的距离等于 b （圆规）。

56．前条练习问题的 7，不用分度器，只用直尺利圆规，也可以作解答如次：

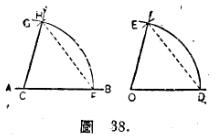
以 α 角即∠ DOE 的顶点 O 做中心，用任意长的半径画圆，设此圆周与两边的交点为 D ， E （圆规）。次以 C 点为中心，作与前半径相同的圆与 CB 的交点为 F （圆规）。次以 F 为中心，以线段 DE 为半径画圆，与前所画圆周之交点为 H （圆规）。

联结 CH （直尺）， CH 即所求之直线。

若问何以∠ BCH =已知角α，则试叠合二图即可知之。

练习问题应用上述的方法以解次题：

1．作已知二角的和及差。

2．作与已知角的二倍、三倍相等的角。

3．任意画一三角形，而作与其三角之和相等的角。 JgySsxPCpja6f0Mbx9EPFS3duTknSW7VznirMMtlLJYnDpSs/m1P8Yzwmlb9cn8M