




“物的问题”,有两方面;一是物理学上的研究,一是哲学上的研究。我此次讲演这个问题,也是从这两方面下手;大约四分之三的时间,是物理学的研究,其余四分之一时间,是哲学方面的讨论。
物理学上的物的观念,到近年来,经了一个大改变。从前的物,是一种占据空间的质体;现在的物,是一个兼含空间时间的事迹(Event)。这种观念改变的原因,就是近来新出的相对说(Theory of Relativity)。相对说是近年的新发明,尤以 德 国物理学者爱恩斯坦(Albert Einstein)阐发的功为最大。他的意思,是说凡运动皆是相对的;宇宙间更无绝对是动,或绝对是静的物体,这种相对的意思,在哲学上已经很古了,不过应用到物理上去,要算是近年的新发明。
爱 氏的相对说又分两个:早一点的,范围狭小一点的一个,叫做特别相对说(Special Theory of Relativity),是一九零五年发表的。后来在 欧 战期间, 爱 氏把相对说的范围,更推广了,这个后来叫做普遍相对说(General Theory of Relativity)。
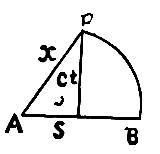
特别相对说的大要,是证明平常所说的空间时间的分别,不过是一种世俗沿用的习惯,实际上并非如此的。我们自来想着,两地间的距离,或者两事间的时候,是一个实在的物理上的数量,其实不然。凡空间或时间的数量,都是依观察人的行动为转移。但是有一件东西,是空间时间组合而成的,名叫“事间”(Interval)。这件东西却和观察的人没有关系。我现在把求事间的算式写出,设如x为两事间的距离,t为两事间的时候,s为事间,就有
s 2 =c 2 t 2 -x 2 (时间-事间)或s 2 =x 2 -c 2 t 2 (空间一事间)
在这两个算式中间,c是光的速度,每秒钟约三〇〇〇〇,〇〇〇,〇〇〇糎。
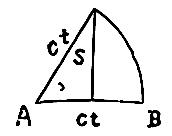
求s的方法,又可用几何作图表明如下:
(一)
(二)
如图(二)作AB线等于x,以A为圆心AB为半径作弧,又由AB线上作垂线等于ct使与圆弧相交得D点,则AD即所求的s。图(二)的作法可以类推。
普遍相对说的大要,在发明一个通律,就是重力新律。这个通律,不但包括 牛顿 的定律(略有改变一点)并且包括能量不灭律,动量不灭律,以及动力学的全部,除了电磁学之外,无一不包括在内,大概说来,凡这个新律,和 牛顿 定律有不对的地方,实验的结果,总是这新律占优胜,照这新律讲起,空间时间的组织,竟是 非欧克里得 。一个质点在空间时间组合中间的运动跡,我们叫做“自然线”(Geodesic),因为他只是顺着自然,那长短是不一定的。
普遍相对说有两个原理:
(一)设两物体的速度,为相对的等速时,则描写自然的诸定律在两物体中必为一样。
(二)上面的公理,无论在那两件物体上都可应用。
要懂得相对说,必定要有许多非常的想象,平常物理上的速度比较起光速来,是很小的。在这些很小的速度里面, 牛顿 式的动力学,是差不多真确的了。但是近年所发明的镭的质点放射,其速度也与兴的速度相差不远。又近年测度的方法,益见精确,就是天文上的速度,若有差错,也可见得。我们现在晓得物质的重量,不是常数,但在运动的方向上,因运动而增加。我们并且晓得一个物体的大小,有因运动而发的理由。这个理由,我随后就加说明。不但如此,世界上没有绝对运动这件东西,凡运动都是相对的。所以自然律令不能说我们能测定绝对运动。 牛顿 的错误,就在这一点。
我们讨论运动,不可把我们的想象,限于地球上的住者,设如我们想象自己住在慧星上,看到太阳系,或者在一个物质的电子上,看到试验室,我们的世界,必然奇怪的了不得。世界原来是奇怪的,平常人不觉奇怪,乃是一个奇怪事体。
平常人以为地球是不动的,天文学家以为太阳,或他恒星,或其他星球世界之中心是不动的。这样的想法都不对。动与静完全是相对的。火车在铁轨上行驶,可以说火车对于铁轨行动,反过来,也可说铁轨对于火车行动。
有一个极重要的实验的结果,为特别相对说所根据的,就是说光的速度无论对于什么物体,都是一样的。这个话又奇怪了!比如有一火车,由车站出发,他的速度是每时六十英里,又有一人,由同地出发,他的速度是每时四英里,那吗,火车对于车站的速度为三十英里,自动车对于车站的速度为六十英里,人对于车站的速度为四英里。倘若自动车与火车相同而行,他们相对的速度,是九十英里,其余的算法,都可以类推。那吗,有一个光线由车站射出,光线对于火车的速度是三〇〇,〇〇〇启罗米突,减二加三十英里吗?对于自动车的速度,是三〇〇,〇〇〇启罗米突减二加二十英里吗?我们想来这是不错的,但是不然。
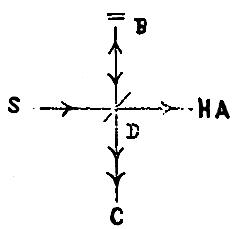
从前的物理学家,把光认为以太中的一种波动。设如地球对于以太的速度是v,那么,光与地球运动的方向相同时,其速度为c-v,相反时,其速度为c+v。譬如一个人在河流中间游泳,顺流的时候,速度必定比逆流的时候大,是一定不易的。 美 国的两个物理学家,叫迈可生,莫尔列(Michelson Morley)的,曾屡次实行以太中光的速度的试验。他们用半透明镜如D接受由S发来的光线,因为D是半透明的,所以光线到D,一部分就反射到B,一部分透过到A。AB是两个反射镜,互为垂直,而且是距离相等的,受了光之后,仍旧射回到D。D是半透明镜,所以受A的反光之后,一部分通过了一部分反到C。受了B的反光之后,一部分反射去了,一部分也通过到C。所以在C的地方,两光仍合成一光。现在把这食品,安置在一个地位,使A的方向与地球公转的方向平行,B的方向和地球公转的方向为垂直。设如光线是以太中的波动,由AB反射回来的光线,应该有迟速的不同;合到C处,就应当生进一步现象的表现。 迈可生 , 莫尔列 的试验,就是应用这个原理。
上面所说光线迟速的原理,很不易明白,我们现在再说一个譬喻。设如有两只船顺流下驶,岸上有一人沿河岸进行,且时常和一只船并着。两船的距离,是两英里;船和人的距离,也是两英里。河流的速度,是每点钟三英里。设如在一定的时候,在一只船上,放出两个鸽子。一个飞到那只船上,然后飞回,一个飞到人的去处,也就飞回。现在的问题,是两个鸽子能同时回到一处吗?
设如鸽子飞的速度,是每点钟五英里,飞往船上的鸽子,去的时候,是5-3=2,每点钟只赶上两英里,但是两船的距离,恰两英里,所以去时,飞到那船的时间,是一点钟。回来的时候,是5+3=8,每点钟可得八英里,二英里的距离,只要一点钟,即十五分钟就够了。故往来一次,总共时间,是一点十五分钟。
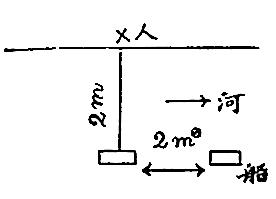
飞往岸上的鸽子,设如所需的全时间为t,则得
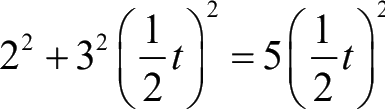
即t=1
故飞往岸上的鸽子,比飞往船上的鸽子,必定先回来。
但是据迈可生,莫尔列的试验,两只鸽子竟是同时回来的!他们试验的装置,完全和鸽子的譬喻同样。设命距离为l,地球在以太中的速度为c,则光向地球运动上往来的时间为
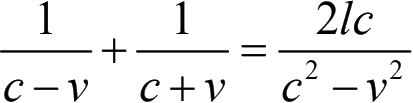 ,而与地球运动成直角方面光波往来的时间,从
,而与地球运动成直角方面光波往来的时间,从
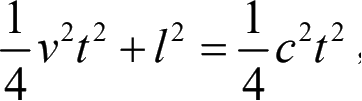 得
得
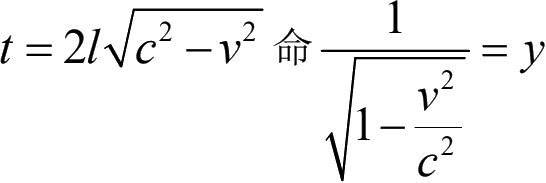
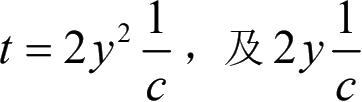
y虽然很小,但是整数,所以
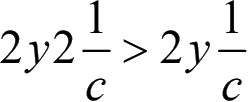 ,即与地球运动方向平行时光行的时间,比与地球运动方向垂直时要长些,但是迈莫两氏试验的结果说不然。
,即与地球运动方向平行时光行的时间,比与地球运动方向垂直时要长些,但是迈莫两氏试验的结果说不然。
这种异样的结果,费慈格纳(Fitzgerad)和罗伦慈(Lorentz)曾有一个解说,这个解说,就是他们的普通缩短说(Theory of General Contraction)。他们以为凡物体有向运动方向缩短的趋向,与运动方向平行的时间,本来应该比运动方向垂直的时间长,但如假设平行方向的物体,缩短了
 ,那吗,应该长出的时间,恰恰与之抵消,所以毕竟没有长短的差别,这种解说,自然完全是一个假设,但是这种假设,在相对说上,是可以成立的。
,那吗,应该长出的时间,恰恰与之抵消,所以毕竟没有长短的差别,这种解说,自然完全是一个假设,但是这种假设,在相对说上,是可以成立的。
许多有关系的物体速度的总和,不是相加的,但比各分速度之总和小一点。比如你在火车的通道上行走,每点钟四英里,你的火车每点钟行三十英里。你对铁路的速度,并不是每钟十四英里,但是稍小一点。
关于这个问题,
费佐
(Fizeau)曾经有一个试验。他用一个很长的玻璃管,装满了水,使光线通过,测定速度,再用流水在管中通过,再测定光的速度。设如光在静水中的速度是w,水流的速度是v,费佐求得光对于水管的速度
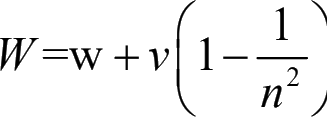 。
。
在这个算式内,n是光的屈折系数等于
 。照罗伦慈的算式,如水流与光行为同向,
。照罗伦慈的算式,如水流与光行为同向,
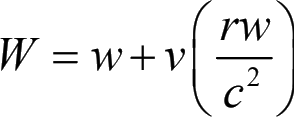 为异向,
为异向,
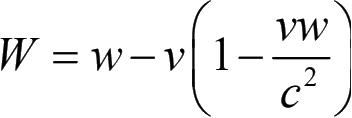 。
。
这方程式是完全由理论上得来的。但是如把这方程推展起来,他同 费佐 的方程式,在观察上必不可免的差误以内,可算是密合的。