下载掌阅APP，畅读海量书库
立即打开
在前一章第三节中我们曾说过，类，往往是辞端。但是，这句话反过来说便不真确，因为辞端有时是个体。我们已经知道，辞端构成命辞底主体——这就是说，在命辞中所说及的东西往往是辞端，这些辞端或者是个体或者是类。所以辞端分为两种：类，与个体。当着我们已经指出一个命辞中的辞端是个体时，我们便将它当做指明有一个分子的类；无论在什么地方这种办法总是可能的。类，在逻辑中根本很重要。
类，并不是逻辑所特有的东西，也是讨论底一般主体。当我们应用具体名称，如猫，兽，人等等时，我们便是在应用类。除了类以外，还有许多性质，如公正，良好，等等，都不是类；只是用来形容类或类底分子。类，并不是用感觉器官所能觉知的一种东西；是我们借以想到我们所觉知的东西的一种程术。类，可以说是一种逻辑的型构（logical construction）但是，这并不是说逻辑是发明显的一种科学；而是说正常的思想之应用合乎逻辑的方法时便要应用类的概念。
当我们在前一章谈到类时，我们已经说过类是分子底集合。不过，这种说法并不完全正确。这种说法之其所以不完全正确的，有两种理由：第一，一个类并不纯粹是分子底集合或总和；第二，还有无分子的类，如圆的方之类（the class of round square），美国底君主，等等。
我们可以问，叫做类的这种逻辑型构是怎样决定了的呢？类，是被种种性质所决定。这就是说，任何性质可以决定一个类，而且具有某种性质的分子便是某个类底分子。例如，理性这种性质决定被有这种性质的一切事物所形成的一个类。人类有理性这种性质——那就是说，人类都是有理性的，所以是属于被这种性质所决定的类，即，有理性的事物之类。在类底意念之中，包含着两个因素：性质或界定性征（defining characteristic）。以及有这种性征的分子。
决定或界定一个类的性征是这个类底内涵（intension）。在另一方面说，一个类底外延（extension）是具有这种性征的分子构成的。将类底内涵和外延之间的区别弄清楚，这是十分重要的事。我们已经假定在逻辑中是讨论类底外延方面，因为至少到现在还没有内涵的逻辑。当着我们谈到类的时候，我们总是预先假定这些类是指着具有界定这个类的性征的分子而言。总而言之，类底逻辑是一种外延的逻辑（extensional logic）。一个类往往包含着一个内涵与一个外延。但是类之对于逻辑底重要方面不是它底性质或内涵；而是具有这种性质的分子，即，外延。
内涵与外延之间的这种区别是相当于古典逻辑中辞端底所谓（connotation）与所指（denotation）之间的区别。既然在这一点上有许多混淆，因此我们在可能范围之内不应用这些作名称，我们必须知道，一个辞端底所谓是它底意义，或是关于它底性质之解释；反之，一个辞端底所指则是关于这个辞端的具有种种性质的分子之解释。
我们知道辞端可以替代类或分子。在一个命辞中的个体为辞端时，那么可以将它当做只有一个分子的类。现在我们要说明辞端有定的类（designating classes）；类可以替代辞端，辞端也可以替代类。
在通常谈话之中，我们常常用“一切”，“有些”等等表型字来形容我们所用的辞端。这些形容辞能够决定一个辞端之是否普及（distribution）。当着一个辞端是指明构成这个类的一切分子时，这个辞端便是普及了。如，在“一切天才底性情都是怪僻的”这个命辞中的类“天才”是普及了，因为这个类中的一切分子都指明了。从另一方面说，在“有些人是刺客”这个命辞中的类“人”没有普及。因为这个类中的分子有一部分被指明了；这里只说有些人是刺客底类之分子，我们必须明了，在以上所举的例样中，“性情怪僻的人”和“刺客”这两个类不能说是普及了，因为我们并不知道这两个辞端是否指着一切分子而言，抑或仅仅指着有些分子而言。在第一个命辞中我们不知道是否“一切天才”构成“性情怪僻的人”之全部外延。同样，假若我们将第二个命辞底辞主改变“一切人”，那么，我们也不知道“一切人”是否构成“刺客”底全部外延。这两个辞端都是不普及的。“没有”这个表型字放一个命底前面往往普及于它所包含着的一切辞端。例如，“没有人有翅膀”，是指明人底整个类与有翅膀的生物底整个类。这个命辞底逻辑意义是，“一切人类是排斥于有翅膀的生物底类之外；”像这样的命辞中的辞端指明它们底全部分子，所以是普及的。
至于没有分子的类，并不是不常有的。比方说，我们能够说“圆的方”是有圆又有方的性质的那些物项之类。这样的类，自然是很特别的，然而这样的类却是实虚的；因为没有个体的事物实际上有又圆又方的性质，徒有其型式而已。这样的类做空类（null class）空类是没有分子的任何类。
当着我们表示空类的时候，我们可以很特别地应用“一切”和“没有”等等表型字。例如，我们能够完全有含意地并且一致地说，“没有圆的方是埃及人底神”，或者说“一切圆的方都是图形”。像这样的说法是可能的，这是因为这些表型字并不必须预先假定有分子存在，或者是涵蕴着分子底存在，从另一方面说，假若我们说，“有些中国底英国皇帝是出身高贵的”，这个命辞必须是错误的，因为“有些”这个表型字包含着它所形容的物项之实际存在，在这个命辞中，预先假定有中国底英国皇帝存在，并且其中有些是出身高贵的。“有些”这个表型字有从一固类底—切分子中选择出一部分分子的作用。假若，那个类中根本没有分子存在，那么应用“有些”这个表型字来表明便是非法。这就是说，当一个辞端是普及了时，便不需要包含着分子底存在；但是当着辞端是被“有些”所形容了，那末便包含分子底存在。
根据上面所讲的，我们可以说有两种解释类底方法。最寻常的方法是预先假定类底分子存在。的确，当着我们讨论一个类底外延之一部分时，我们是预先假定类有分子存在。但是存在与否这个问题，根本是一个事实上的问题，而不是逻辑问题。我们根据法律可以判定有某种性质的一切犯法者必须受处罚。这个法律底意义无异于说不实际上究竟是否有所指的这个类底分子在，在“有某种性质的犯法者”这个类与“受处罚的人”这个类之间的关系是显然易明的；与存在问题完全没有关系。依此，解释类底两种方法可以叫做通常方法与最少方法。通常的解释（ordinary interpretation）是预先假定分子底存在，而“最少的”解释（minimum interpretation）是将类看做空虚的。
对于辞端或类底这两种解释是十分重要的。在后面一章中，我们将会知道推论底可能性是大部分以采取那一种解释为依据。通常我们大都采取最少的解释。但是，有些事例必须采取存在的或通常的解释，如，“有些”在其前面的命辞，或者显明说某命辞实际有分子存在的情形，便是除此以外，我们便不可假定类有什么分子实际存在。
在寻常的讨论中，我们很少指称普遍的类；而多指称特殊的类。一切具体辞端都是特殊的类之用语言所表出者，如，“船”’，“政客”，“食物”，“信用”，“暴徒”，“神仙”，“器具”等等，都是代表某些特殊的类的辞端。如我们在前面所着重地说过了的，逻辑底自身不研究个别的特殊的讨论；而只研究讨论底型式，我们已经说过，论式之型式的性征必须在关系中才能发现同样，逻辑只研究普遍的类所有的种种关系与型式：而不理会它底个别特殊事实，即，不理会任何特殊的类。
依照要显示许多类之间的普遍关系的这种要求，于是构作一种逻辑底代值学（algebra of logic），或更妥当地说，构作一种类底演算（calculus of classes）。在前一章我们已经讲过命辞底符示。用符号来表示在型式方面对于命辞的研究便是“命辞底演算”（calculus of propositions）。同样，用符号来表示许多类之间的型式性质及其关系，便是“类底演算”如我们将会在本书第二部中所讲到的，命辞与类底这种研究完全是近似数学性质的。
我们将要等到在本书底第二部分中来讨论当做一个系统的类底代值学。现在我们只简单地给与这种符号以基本的解释；因为这种符号对于逻辑底重要和效用实在是难以言状。
小楷字母“a”，“b”，“c”等等是用来替代任何类。相等记号“=”底意义与通常在数学中的意义一样。相等是一种关系，如假若a=b，b=a，那么这两个项目便是同一的。假若a=b，那么“a”类底分子便与“b”类底分子是同一的。乘号，“×”，表示互为分子。这就是说，“a×b”底意义是这个类又是“a”又是“b”。加号“+”底意义是“或”如，“a+b”底意义为是“a”或是“b”的物项之类。减号“－”表示否定；如“a×－b”底意义是“a”类是“非b”’。零“0”简单地表示没有分子的类。“I”替代“讨论界域”（universe of discourse）。讨论界域底意义我们将要在后面讲解。我们现在例示这些符号：
a——“a”类
－a——“非a”类
ab——“又是a而且又是b”底类。a与b之间的乘号并不时常写出。替代类的符号写在一起，那么便假定已有了乘号。
a－b——“又是a而且又是非b”底类。
a+b——“或为a或为b”底类。
我们必须记忆，“或”底意义不是必须互相排外的。这个符式可以更精密地解释为“或为a或为b或为a与两b两者”的类。
a+－b——“或为a或为非b或为a与非b两者”的类。
0——空类
I——零底否定。这个类是包含着一切分子——宇宙——的类。0 与I都是单类（unique classes）。
a=0——“a”类是空的，完全没有分子。
a≠0——“a”类有分子。画一条斜线在等号之上来否定等号，以表示“a”不等于零。
a=b——“a”类与“b”类相同。比方说，等边三角形底类是等于等角三角形底类。因为是们底分子是相同的。
以上都是类底演算中的基本概念。我们可以根据这一点来陈述并且解说这种代值学底许多命辞。我们将会在以后看见类底这种演算的确是可以解释异于类的物项的一种普遍代值学。然而我们只解释类，并且仅仅认定它是一种代值学或类底演算；至少现在是如此。
ab=ba——“又是a而且又是b”的类等于“又是b而且又是a”的类。设“a”代表人类，“b”代表学习的动物。那么是人类又是学习的动物的那种东西与是学习的动物又是人类的那种东西相同。这也就是说，这两个类是相等的。
a×0=0——设“a”代表猫类。那么，又是猫而且又是无何有的物项底类是无何有；或者等于无何有的猫类便是无何有。
a+I=I——是“a”或是“任何物”的东西便是“任何物”设“a”代表灰盘；于是或为灰盘或为任何物的东西至少是任何物。
a+a=a——在这种代值学中没有数字的系数。设“a”代表书，那么或者是一本书或者是一本书的东西便是一本书。
我们无需在这里将这种代值学中的一切命辞都加以讨论。此时要紧的事是必须能够读这种种符式与符号。我们现在来说明几个简单的断定命辞：
ab=0——没有“a”是“b”。这就是说，又是“a”而又是“b”的类是空的。设“a”代表人，“b”代表天使。又是人而又是天使的这种东西底类没有分子。简单地说，就是，没有人是天使。
ab≠0——又是“a”而又是“b”的类不是空虚的：即，有些“a’s”是“b’s”。设“a”为政客，“b”为不诚实的人，那么，这个符式可以读作：“有些政客不诚实。”
a·b=0——“a”为“非b”便是空的，没有分子。即，凡“a”为“b”。设“a”代替长方形，“b”代替图形。那么，不是图形的长方形便不存在；或者是一切长方形都是图形。
这种符式可以给予我们将要用来叙述型式逻辑的类以一种精密的与通扩的（generalized）检讨。读者必须能够认识这些符号并且了解符示了的类之间的种种关系；因它们对于逻辑十分重要。
除了应用符式来表明类的关系以外，还有一种表明类的关系底方法，这种方法就是图示法，图示法底优点就在能简便而明显地将类之间的一般关系表示出来。
在前一节里，我们会说及“讨论界域”，又会说过“I”是表示讨论界域的一个符号。讨论界域是一个单类，这个单类以一切事物为其外延。我们且列举人这个类为例样。关于这个类的讨论界域可以认为是：包含着是人和非人的类。这样一来，就含盖着我们所能想像得到的任何物项。任何物项必定或是“人”底一个分子或是“非人”底一个分子。比方说，山岳，教室，鹄，负一底平方根，墨水，彗星，青蛙等等东西都属于这个讨论界域之中，因为它们都是“非人”这个类底分子。美国陆军官员，国王，航空员也都属于这个界域，因为他们至少是“人”这个类底外延之一部分。但是我们已经指明关于一个特殊类的讨论界域。讨论界域所型式地考究的是什么呢？即，什么与任何所说的类各自独立呢？型式地界定起来，讨论界域就是包含着一个类底全部外延及其矛盾的那种单类。所以，为“a”（任何类）或为“－a”（非a的类）的任何类是I（讨论界域）。如，黄色东西底类与绿色东西底类便不能决定一个讨论界域，因为这两个类不相矛盾。黄与非黄，绿与非绿才是相矛盾。所谓矛盾，不独互相排外，而且又共同尽举。黄与绿互相排外，但不共同尽举，一个东西必须是或黄或不黄，但不必是或为黄或为绿；也许为红或蓝，或其他任何颜色。前者为矛盾（contradictory），后者相反（contrary）。“讨论界域”这个名称往往用得很混淆，有时是指着异于界说所界定的某种事物而言。然而在这里除了指明被界定为任何一对相矛盾的类之选取的这种意义以外，在任何其他意义之中，我们都不理会它底用法。
我们现在用图形表示这些类，设有一个类“a”，我们可以将它画作一个圆圈如下：
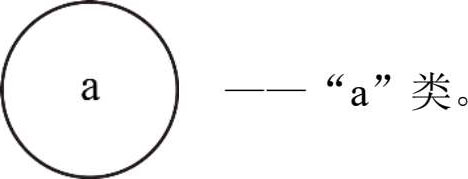
于是，我们可将讨论界域画做一个包含着“a”的方形或长方形，如：
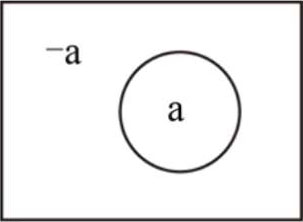
在圆圈之内的领域可以解释为“a”类底外延。在圆圈之外，方形或长方形之内的领域是“非a”或“a”底矛盾（－a）这两者合并起来便构成整个的讨论界域。这就是说，讨论界域是在方形或长方形之内的整个领域。
此外，可以包含“b”类，并且将“b”类画做与“a”类相叠，如：
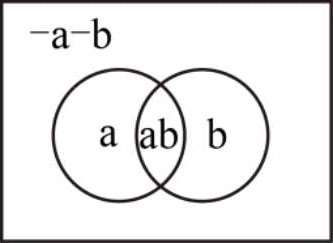
在圆圈中没有重叠着的领域各别地代表“a”与“b”在圆圈中的重叠部分为又是“a”而且又是“b”底类。在圆圈之外而在是方形之内是“a”与“b”底矛盾之领域。在长方形之内的领域共同构成I或讨论界域。任何可觉知的对象必须属于这个界域中的某一部分。我们现在用相同的语言的，代值学的，以及图示的方法来表示类。涂以黑点的部分是在每种情形中用符号所表出来的部分。
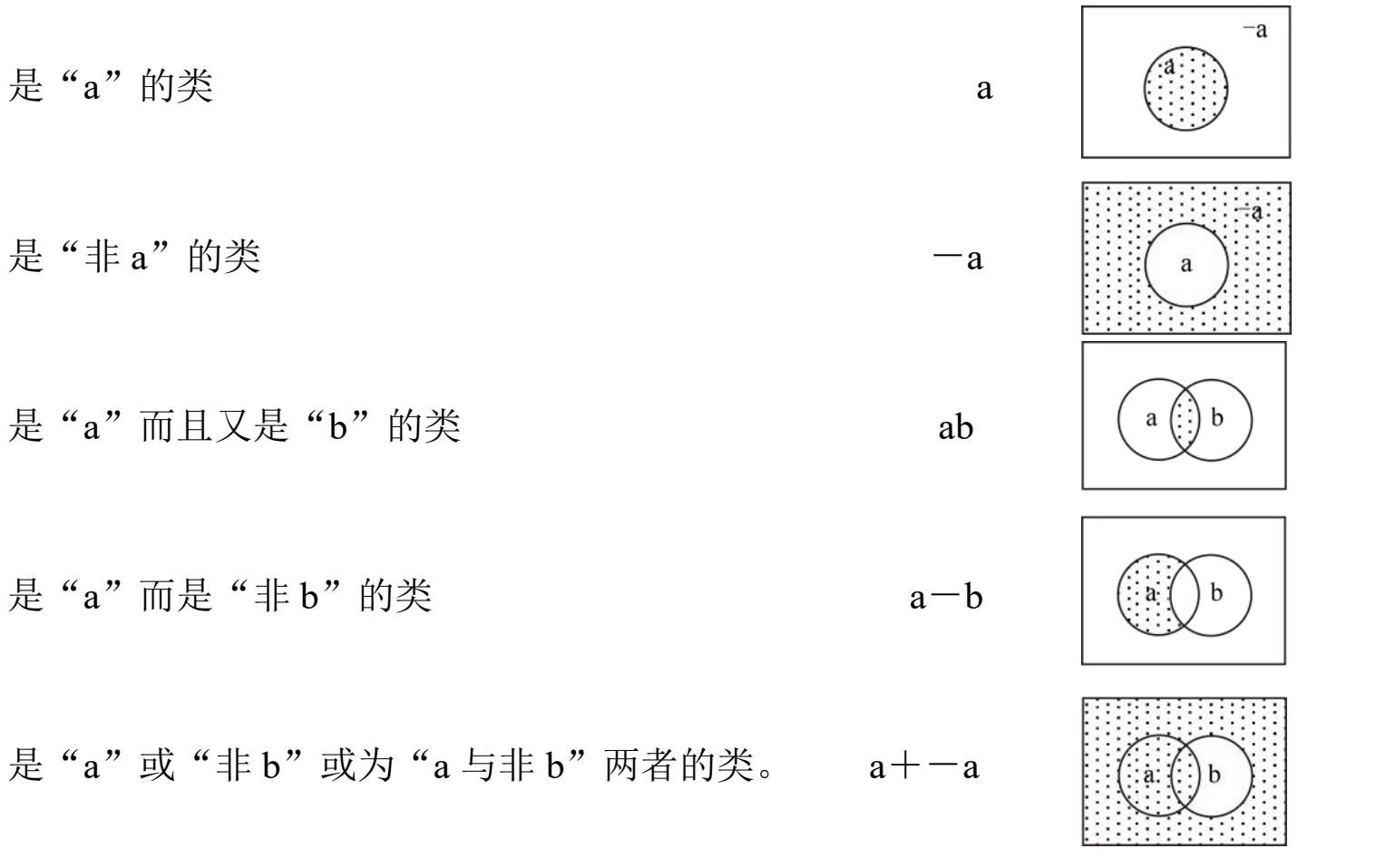
空类0
包含着一切事物——宇宙——的单类I
“a”类不等于零——它有分子。a≠0
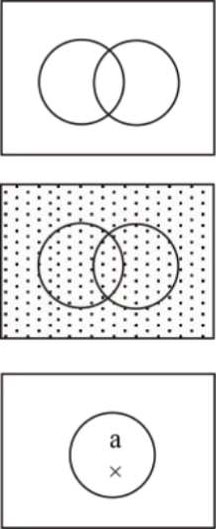
（在所指的类底领域中的那个叉号之意义是“至少有些。”）
这些图解表示我们在本章第三节中所讨论的许多概念。我们现在图示几个简单的断定命辞如下：
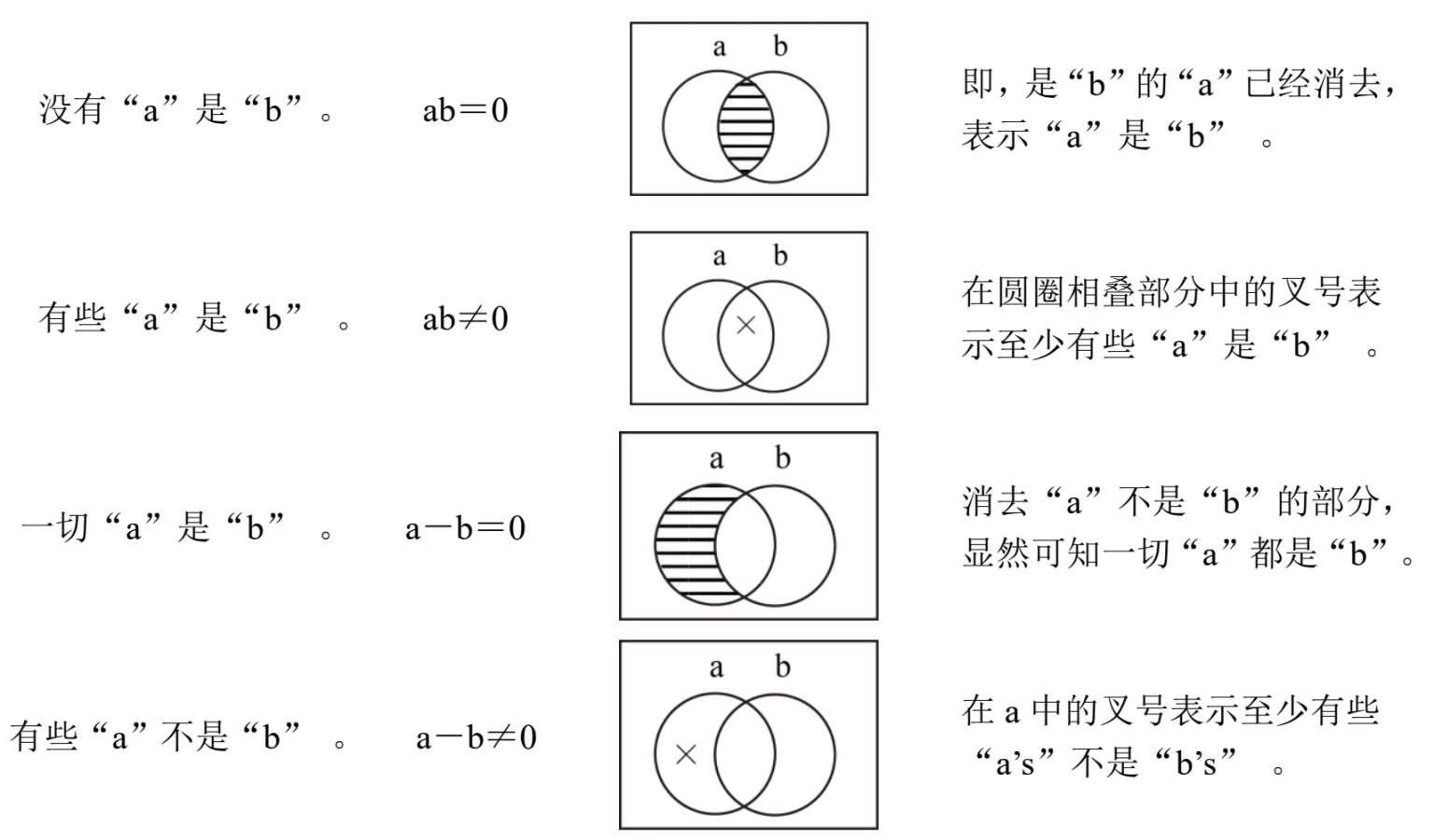
以上的图解是范恩（Venn）所构作的
，通常叫做“范恩图解”（Venn diagrams）。当我们讨论三段式时，我们将会知道这些图解可以便利地表明三个类之间的种种关系。可是，在三个类以上，这种图解便很拙劣，因而失掉了效用。这些图解之最大便利是简洁地并且精确地直接表出三个类那样多的类之间的一切可能关系。这种图解对于初学逻辑的学生之帮助，正犹之乎黑板与粉笔对于几何学家底帮助一样。
辞端是类，或者是个体，当着命辞中有个体时，我们可以将它们当做仅仅有一个分子的类；除了不能施行这种办法以外。逻辑所讨论的命辞之根本主体终究是类。类，有一个内涵与一个外延。一个类底内涵是界定它的性征。反之，外延是具有这种性征的分子。逻辑是讨论在外延方面的类。辞端替代类，而且当着辞端指称它们底全部外延（例如，一切人）时，那末它们便是普及的。当着辞端仅仅指称它们底外延之一部分（例如，有些人，少许人，等等）时，那末它们便没有普及。没有分子的类（例如，半人牛马的怪物类，或独眼神），便是空类。类，像命辞一样，也可以符示出来；因此，可以型式地并且精确地研究之。这已经在第三节中讨论了少许。类也可以用范恩图解表示出来，范恩图解可以精确地在空间里表示许多类之间的关系底代值学的程式。应用这些图解底目的是帮助我们清晰地表示型式地研究了的类之间的种种关系。我们可以在这里补充地说一句，类之间的许多关系往往是他们底内涵或外延之间的关系。