




X→ P-T-G ; X → L o 1 → L o2 → L o3 ;{P,T,G}=X/{Lo1,Lo2,Lo3}=X/Lok;
黎曼猜想本意与素数定理(PNT):π(X)=Np=X/Lo1;(黎曼欲证本文将证!)
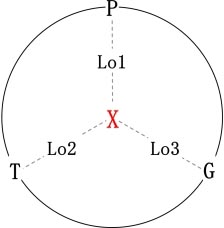
图1 顶层设计图
图中,X为偶数公共边界,P,T,G(PP,TP,GP)为净素数孪生横队及哥猜竖对,由X/Lok 得到。Lok={Lo1,Lo2,Lo3},称为函数桥,素数桥,分母桥,或通商桥,Lok由筛法得到。{P,T,G}=X/Lok是顶层目标的全部数学表达式,其中Lo1第一桥解决素数定理Np是主要矛盾。
引理0:算术基本定理,体现整数堆垒性构成法则(引理0略)。
引理1:滤波筛法定理,体现整数整除性判素法则:判奇偶素合与变参。也称判素定理。
引理1全称滤波筛法判素定理。
整数X,若不能被素数2,3,5…Z=PR≤√X整除,则X必素。(反证法证略)
判素式:P(X)=Π X%P≠0;或P(X)=Π X%P!=0;(P∈2,3,5…Z=PR≤√X)
筛法判奇偶素合,解决了百年难题;O(X)=X%2!=0;E(X)=X%2==0;P(X)=Π X%P!=0;C(X)=!P(X)=∑ X%P==0;
符号约定:一般x,X为变量或整数偶数,y,Y为函数与分布;Z=PR=√X;P,K为滤波因子或参数系数;P,T,G,B小写作下标大写表数目。模余借C语言mod或%,|表对称被整除,!表异称不被整除,==等于,!=与≠不等于;
!P非P;P!定义素数阶乘:P!=P1P2P3P4P5;或程序中略有不同。P1Πj=2,P2Πj=3…可略写下标为P1Π,P2Π…;Ro:Recursive Outward外推式递归;τμ稀密度互逆,τ直接与㏑X对比;因大多数公式都经计算机辅助计算检验(CACAP),故以C语言形式语句表达更简单直接;易于自明不必拘泥;传统数学也应借鉴。
X,n,p,z为实数,自然数,素数及筛法必要界等,与传统数论通用易明。
特别注意证明计算平台:人工“草稿纸”与机器“累加器”本质,克服自由化,提倡范式化!
首先梳理数学数论人物序史,作为讨论黎曼猜想金钥匙的前导。
年代 人物 进展(素数问题猜想)
B.C.
330-275(55)欧几里得 反证法证明素数无穷多
275-194(81)埃拉托色尼 ES筛法寻找素数
A.D.
1643-1727(84)牛顿
1646-1716(70)莱布尼茨 牛莱微积分
1690-1764(74)哥德巴赫 1742年著名哥德巴赫猜想
1707-1783(76)欧拉 欧拉公式函数级数sin,cos,log,mod,但缺莫非它“%-!-|”底层逻辑链符号?
1752-1833(81)勒让德π(X)=X/㏑X-1.08366,π(X)=X/㏑X称为对数素数定理;
1777-1855(78)高斯π(X)=X/㏑X-1 =X/㏑(X/e),高斯猜想最佳素数定理待证!
1826-1866(40)黎曼 黎曼是高斯和狄里克雷的后继者,黎曼假设“金钥匙”未证;
1859黎曼“论小于给定数X的素数个数”尝试证明素数定理(PNT);
1896阿达玛、德拉瓦 正式开启首次证明连续对数素数定理:π(X)=X/㏑X;
1900维纳 再次证明素数定理
1900希尔伯特“23.8”即23类之第8类难题:“四色、费玛、黎猜、孪猜、哥猜”
1879-1955(76)爱因斯坦“相对论”
1901-1976(75)海森堡“不确定性”
1906-1978(72)哥德尔“不完备性”
1948塞尔伯格、艾尔多思,再次证明素数定理π(X)=X/㏑X
1980纽曼(Newman)再次证明素数定理π(X)=X/㏑X
1987陈景润 再次证明素数定理π(X)=X/㏑X及Lo1=Π P/(P-1)未用;
欧拉、黎曼也证明过Lo1=Π P/(P-1),定义域没有明确,误差较大;
2010 潘承彪及《哈代数论(第6版)》均说应该寻求更好更简单的“初等证明”;