




统计是描述研究、相关研究和实验研究中的重要研究工具,帮助我们观察和解释肉眼可能错过的事物。准确地理解统计能够令所有人获益匪浅。如今,能够将简单统计学原理应用于日常推理是受过良好教育的体现。人们不需要记住复杂的公式,就可以更清晰、更具批判性地考虑数据。
凭空估计往往会误判实际结果,进而误导公众。只要有人提出一个较大的、笼统的数字,而其他人对此表示赞同,用不了多久,这一数字就会成为误导公众的错误信息。请看下列三个例子:
·同性恋占总人口的10%,还是像各种全国性调查所表明的占总人口的2%~4%(见第11章)?
·我们只使用了10%的大脑,还是使用了近乎100%的大脑(见第2章)?
·每天走10 000步能够让人更健康,还是8500步或13 000步也行?游泳或慢跑可以吗(Mull, 2019)?
设定目标时,人们都喜欢较大的、笼统的数字。在减肥时,人们更倾向于减掉10千克,而不是9.07千克。棒球击球手在赛季结束前会冲刺提高平均打击率,使得他们平均打击率达到0.33的可能性比达到0.299的可能性高出近四倍。(Pope & Simonsohn, 2011)
看到耸人听闻的标题,却没有证据支撑时(如全国有100万青少年怀孕,200万老人无家可归,或300万起车祸与酒精有关等),你就可以非常肯定地知道,这是有人在猜测。猜测者若是想强调这个问题,就会往更大的数字去猜;若是想尽量减少问题,就会往更小的数字去猜。要记住的一点:面对没有证据支撑的较大的、笼统的数字,要进行批判性思考。
虚假统计还会引发无谓的健康恐慌(Gigerenzer, 2010)。20世纪90年代,英国媒体曾报道一项研究,表示服用某种避孕药的妇女患血栓的风险增长了100%,而血栓可能引发中风。这篇报道广为流传,引起成千上万的妇女停用避孕药,结果导致了一大拨意外怀孕,还有估计13 000例额外的流产(这也与血栓风险增加有关)。由于这一较大的、笼统的数字的诱导,很少有人关注这项研究的实际结果:血栓风险的确增长了100%,但只是从七千分之一增长到了七千分之二。这样的虚假警报表明,我们有必要进行批判性思考,教授统计推理知识,并且更透明地展示统计信息。
学习目标问题 1-12 我们如何使用三种集中量数来描述数据?两种差异量数的相对效用是什么?
研究人员采集完数据,可以采取描述性统计来对数据进行整理,将数据转换成简单的条形图正是这类方法之一。如图1.8所示,该图展示了十年后仍在道路上行驶的不同品牌卡车的数据分布情况。观察这样的统计图时,我们要格外注意。要设计一个令差异看起来明显(图1.8a)或不明显(图1.8b)的图表是很容易的,关键在于如何标注纵向刻度(Y轴)。
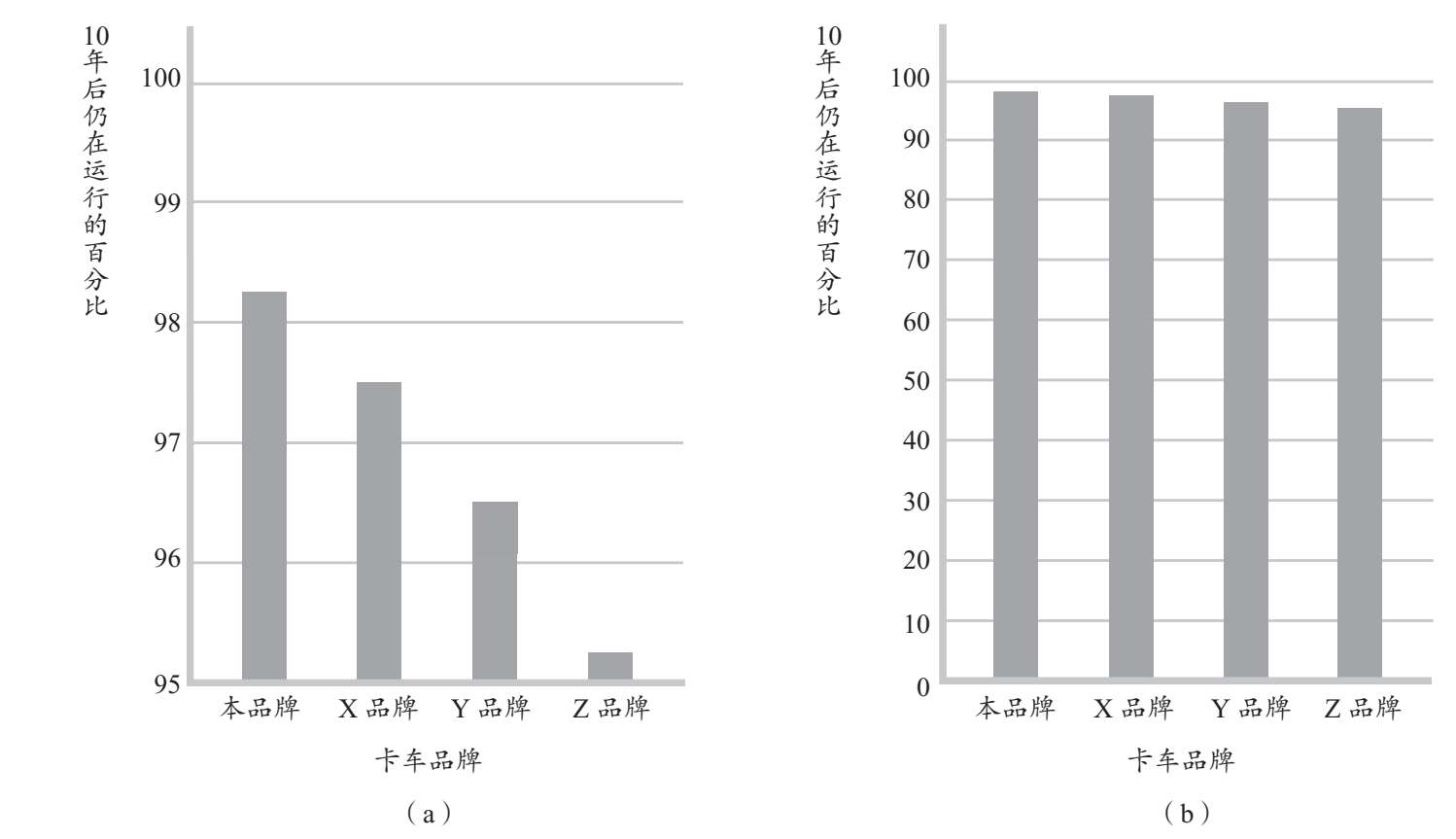
图1.8 观察刻度标签
要记住的一点:我们要聪明地思考。在解释图表时,要考虑刻度标签,注意刻度范围。
自问
你有没有在课堂上、论文中,或者与朋友或家人讨论时,用统计说明某一问题的经历?回想一下,你引用的数据是否准确可信?你怎么知道这一点?
检索练习
RP-1 图1.8的图(a)由一家卡车制造商提供,图中包含实际的品牌名称,表明其卡车的耐用性更佳。关于不同品牌卡车的耐用性,图(b)说明了什么?这是如何做到的?
答案见附录D
接下来则是通过集中趋势测量对数据进行概括,即用一个数值来代表整组数值。最简单的测量方法是 众数 (mode),即出现频率最高的一个或多个数值。我们最熟悉的方法是 平均数 (mean,或算术平均数),即所有数值的总和除以数值的个数。而 中位数 (median)则是位于中点(第50个百分位)的那个数值。在分隔的高速公路上,中央隔离带处于中间位置,对数据而言也是如此。如果将所有数值从高到低进行排列,一半数值会在中位数之上,另一半数值会在中位数之下。
众数:一组数据中出现频率最高的一个或多个数值。
平均数:一组数据的算术平均数,通过将全部数值相加后再除以数值的个数得到。
中位数:一组数据中位于中间的那个数值;一半的数值比它大,另一半比它小。
集中量数简明地概括了数据。但是,分布不平衡时(因为几个异常数值而产生偏态),平均数会发生什么变化?以收入数据为例,众数、中位数和平均数往往讲述了截然不同的故事(图1.9),这是因为平均数会受到少数极端收入的影响而发生偏差。当亚马逊创始人杰夫·贝佐斯(Jeff Bezos)进入一家小咖啡馆时,其他顾客立刻成了(平均数意义上的)亿万富翁,但顾客们财富的中位数并没有变化。
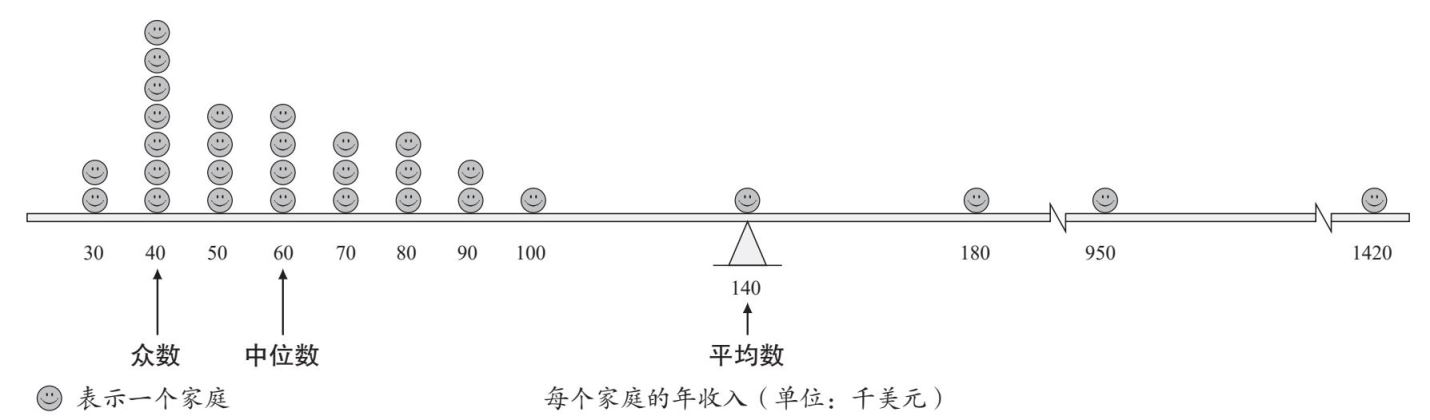
图1.9 偏态分布
这一收入分布图说明了集中趋势的三个测量标准:众数、中位数和平均数。请注意,仅需几个高收入家庭就能令平均数(平衡高低收入的支点)显得很高。
理解了这一点,你就能明白为什么2010年美国人口普查时近65%的美国家庭的收入“低于平均水平”,处于底层的一半挣钱者的收入远低于全国总收入的一半。因此,大部分美国人的收入低于平均水平(平均数)。平均数和中位数反映的真实故事截然不同。
要记住的一点:一定要注意报告的是哪种集中量数。如果是平均数,请考虑一些非典型的数值是否会令其产生偏差。
一个恰当的集中量数可以告诉我们很多东西,但这个单一的数字也会忽略许多其他信息。而了解数据的变异性(数据的相似性或差异性)则会有所帮助。由低变异性数据得出的平均值比基于高变异性数据的平均值更可靠。假如在本赛季的前10场比赛中,某篮球运动员每场比赛的得分都在13到17分之间。了解这一点后,我们更相信该运动员下一场比赛中的得分会在15分左右,而非5分到25分不等。
数值的 全距 (range,最小值和最大值之间的差距)只是对变化的粗略估计。在其他类似群体中,如果有几个极端数值,如图1.9中的950 000美元和1 420 000美元的收入,就会令数值范围出奇地大。
全距:分布中最小值和最大值之间的差距。
标准差:测量数值在平均数周围变化程度的计算方法。
测量数值之间偏离(差异)程度的更有效标准是 标准差 (standard deviation),它会使用所有数值的信息,能够更好地测量数值是集中还是分散。该计算公式 [1] 收集了有关单个数值与平均数的差异程度的信息,可以很好地说明问题。比如,A班和B班考试成绩的平均数相同(75分),标准差却迥然不同(A班为5.0,B班为15.0)。你是否有过这样的考试经历,一门课程有三分之二的同学成绩在70分至80分之间,而另一门课程的成绩则更加分散(三分之二的同学成绩在60分至90分之间)?标准差和平均成绩会准确地告诉我们每个班级的实际情况。
思考数值的自然分布趋势,你就会理解标准差的含义。数量较大的数据,如身高、智力分数或预期寿命等,通常会呈对称的钟形分布:大部分数值都落在平均数附近,只有较少数值落在两个极端附近。这种钟形分布非常典型,我们将其形成的曲线称为 正态曲线 (normal curve)。
正态曲线:一种对称的钟形曲线,可用于描述多种类型数据的分布情况;大多数数值都分布在平均数附近(约68%的数值位于一个标准差之内),越靠近极端位置的数值分布越少。正态曲线也称为正态分布。
如图1.10所示,正态曲线一个有用的属性在于,大约68%的个案都落在平均数两侧一个标准差的范围内,大约95%的个案落在两个标准差的范围内。因此,正如本书第10章显示的,大约68%的人的智力测验分数在100±15分的范围内,大约95%的人的测验分数在100±30分的范围内。
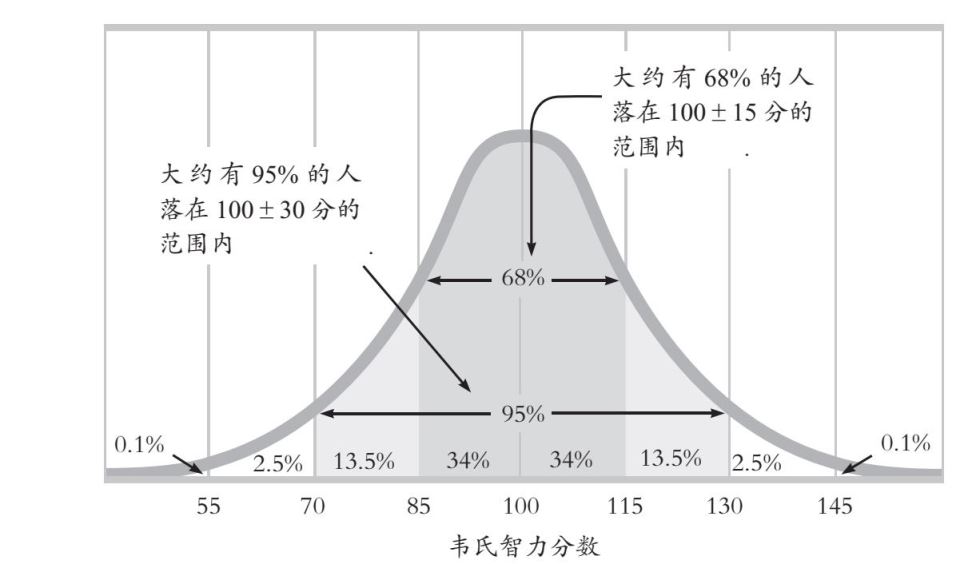
图1.10 正态曲线
能力测验的分数往往围绕着平均数形成一条正态曲线。以韦氏智力量表为例,其平均得分是100分。
检索练习
RP-2 数值分布的平均值是___,出现频率最高的数值是___,一半数值比它大、一半数值比它小的数值中间值是___。我们确定数值围绕平均数变化的程度,需要有关数值的____,需要使用___公式。
答案见附录D
学习目标问题 1-13 我们如何知道观察到的差异是否可推广到其他人群?
数据是“嘈杂的”。在我们前面提到的实验中,那些停用脸书账户的人患抑郁症的平均数与那些没有停用的人的平均数截然不同,这并不是因为两者之间存在任何真实的差异,只是因为被抽样者的偶然波动。那么,我们能有多大把握推论观察到的差异不是研究样本的偶然结果呢?我们可以探寻差异的可靠性和统计显著性,以此作为指导。这些推论统计能够帮助我们确定观察结果是否可用于推广到更大的样本总体(被研究群体中的所有人员)。
根据样本进行推广时,我们应该牢记三个原则:
1.代表性样本优于偏态(非代表性)样本。 归纳的最佳依据不是那些特殊而深刻的案例,而是代表性案例。科学研究从来不会对整个人类总体进行随机抽样。因此,要牢记一项研究的样本人群类型。
2.低变异性观察结果比高变异性观察结果更可靠。 正如前文所述,某篮球运动员的每场比赛得分都十分稳定,基于低变异性数据的平均数更可靠。
3.研究案例越多越好。 一位求学心切的准大学生前往两所大学参观,各用了一天时间。在第一所大学,该学生随机听了两堂课,发现两位老师都非常幽默,很有吸引力;而在第二所大学,抽取的两位老师似乎都很沉闷,没有吸引力。回到家后,他没有发现每个院校只抽查两名老师的样本规模太小,而是和朋友们聊起了第一所学校的“好老师”和第二所学校的“无聊家伙”。同样,我们知道这一点,却也常常忽略了它:基于多数案例的平均数要比仅基于少数案例的平均数更可靠(变异性更低)。发现小规模学校在办学最成功的学校中占比极高后,一些基金会立马投资将大规模学校拆分为小规模学校,却没有意识到小规模学校在办学最失败的学校中占比也极高,因为学生较少的学校办学成果变化更大(Nisbett, 2015)。同样,研究案例较多时,平均数会更可靠,研究也会更具可复制性。
要记住的一点:聪明的思考者不会受一些逸事的影响。基于少数非代表性案例的概括是不可靠的。
假如你对攻击性测试中男性和女性的得分进行了比较,发现男性表现得比女性更具攻击性。但每个个体都是不同的,你观察到的性别差异只是一种偶然情况的可能性有多大?
研究人员会采用统计方法来回答这一问题。统计测试首先假设被研究的群体之间不存在差异,这一假设称为零假设。通过统计数据,我们可以得出结论,观察到的性别差异太大,不太可能符合零假设。因此,我们会放弃零假设(不存在差异),认为这个结果具有 统计显著性 (statistically significant)。这一巨大差异为备择假设提供了支撑。备择假设即被研究的群体(如男性和女性)之间在某方面(如攻击性)确实存在差异。
统计显著性:假设被研究的群体间不存在差异的情况下,某一结果(如样本间差异)为偶然发生的可能性。
两组之间的差异大小(效应量大小)是如何决定统计显著性的呢?首先,如果两个样本的平均数都是对各自群体的可靠测量(如每个样本都基于多数低变异性观察结果),那么这两个样本之间的任何差异都更可能具有统计显著性。就上述例子而言,女性和男性攻击性测试得分的变异性越低,我们对观察到性别差异的真实性就越有把握。样本平均数之间的差异很大时,只要样本是基于多次观察的结果,我们同样会对这一差异反映了两个群体间的真正差异更有把握。
简而言之,样本规模以及样本之间的差异较大时,我们就可以说这样的差异具有统计显著性,这意味着我们观察到的差异可能不只是样本之间的偶然变异,并且我们也可以放弃零假设。
心理学家对统计显著性的判断非常保守,他们就像陪审团一样,在证明被告有罪之前必须假定其无罪。许多心理测试会给定 p 值,这一数值是给定样本数据的情况下零假设为真的概率。对于大多数心理学家来说,排除合理怀疑的证明没有多少意义,除非零假设为真的概率( p 值)小于5%( p < 0.05)。而一些研究人员认为,统计显著性被过分强调了,“不显著的”结果并不意味着组间差异完全不存在(正如人们经常假设的那样)(Amrhein et al., 2019),它只是表明了更大的不确定性。目前,许多心理学家仍在继续使用 p < 0.05的原则,但我们要对此保持关注。
在学习如何做研究时,我们应该牢记,即使样本足够大或足够同质,各研究群组之间的差异仍可能具备“统计显著性”,却没有什么实际意义。它们在统计学上是“显著的”,但效应量很小。对数十万头生子和后生子的智力测试分数进行比较,发现头生子的平均分数要高于后生的兄弟姐妹,这一趋势十分显著(Rohrer et al., 2015; Zajonc & Markus, 1975)。但是,由于这些分数的差别很小,这一“显著”差异产生的效应很小,没有什么实际意义。
要记住的一点:统计显著性只表明在零假设为真的情况下某结果偶然发生的可能性,但并不说明该结果具有任何重要性。
自问
你有被写作者或演讲者尝试用统计数字欺骗的经历吗?在这一章中你学到的哪些知识对今后避免上当最有帮助?
检索练习
RP-3 你能解决这个难题吗?
密歇根大学学生办公室发现,在第一学期结束时,通常有约100名文科和理科学生拿到满分。然而,能够以满分毕业的学生只有大约10至15名。你认为对这一现象最可能的解释是什么(Jepson et al., 1983)?
RP-4 _____统计总结数据,而_____统计则决定了数据是否可被推广到其他群体。
答案见附录D
[1]
样本标准差公式:样本标准差=
 。
。